Някои точки за това как се извършва решението на неравенствата
Една от темите, която изисква максимално внимание и постоянство от страна на студентите, е решаването на неравенствата. Подобни на уравненията и в същото време много различни от тях. Защото тяхното решение изисква специален подход.
Имоти, които ще са необходими за намиране на отговора
Всички те се използват за замяна на съществуващия запис с еквивалент. Повечето от тях са подобни на тези в уравненията. Но има различия.
- Функция, която е дефинирана в LDU, или всеки номер може да бъде добавена към двете страни на първоначалното неравенство.
- По подобен начин е възможно умножение, но само чрез положителна функция или число.
- Ако това действие се извършва с отрицателна функция или число, тогава знакът на неравенството трябва да бъде заменен с обратния.
- Функциите, които не са отрицателни, могат да бъдат повишени до положителна сила.
Понякога решението на неравенствата се придружава от действия, които дават външни отговори. Те трябва да бъдат премахнати чрез сравняване на домейна на DHS и различни решения.
Използване на метода за разстояние
Неговата същност е да намали неравенството в уравнението, в което в дясната страна е нула.
- Определете областта, в която лежат валидните стойности на променливите, т.е. LDL.
- Преобразувайте неравенството с помощта на математически операции, така че в дясната му част да има нула.
- Заменете знака за неравенство с “=” и решете съответното уравнение.
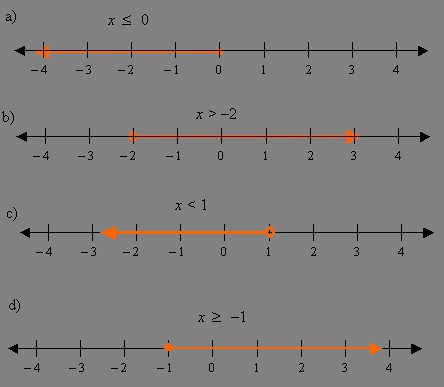
- На цифровата ос маркирайте всички отговори, получени по време на решението, както и интервалите на TLD. Със строго неравенство на точката, която трябва да нарисувате пробита. Ако има знак за равенство, тогава те трябва да боядисат.
- Определете знака на оригиналната функция на всеки интервал, получен от точките на LDD и разделяйки отговорите му. Ако при прехода през точката знакът на функцията не се промени, то той влиза в отговора. В противен случай - изключени.
- Граничните точки за TLD трябва да бъдат допълнително проверени и само след това да бъдат включени или не в отговора.
- Отговорът, който се получава, трябва да бъде написан под формата на обединени множества.
Малко за двойните неравенства
Те използват два знака за неравенство в записа. Това означава, че някои функции са ограничени от условията веднага два пъти. Такива неравенства се решават като система от две, когато оригиналът е разделен на части. И в интервалния метод се посочват отговорите от решението на двете уравнения.
За разрешаването им, също така е допустимо да се използват посочените по-горе свойства. С тяхна помощ е удобно да се намали неравенството до равенство нула.

Каква е ситуацията с неравенствата, в които има модул?
В този случай, решението на неравенствата използва следните свойства и те са верни за положителна стойност на "а".
Ако "x" приема алгебричен израз, тогава такива замествания са верни:
- | x | <a до -a <x <a;
- | x | > a на x <-a или x> a.
Ако неравенствата не са строги, тогава и формулите са верни, само в тях, с изключение на знака повече или по-малко, се появява "=".
Как да се реши система от неравенства?
Това знание ще се изисква в случаите, когато такава задача е дадена или има запис на двойно неравенство или се появява модул в записа. В такава ситуация решението биха били стойностите на променливите, които биха удовлетворили всички неравенства в записа. Ако няма такива номера, системата няма решения.
Планът за решаване на системата от неравенства:
- решава всеки от тях поотделно;
- начертайте всички интервали по цифровата ос и определете техните пресичания;
- напишете отговора на системата, която ще бъде обединението на случилото се във втория параграф.
Как да се справим с частичните неравенства?
Тъй като при тяхното решаване може да се наложи да се промени знака на неравенството, е необходимо внимателно и внимателно да се изпълнят всички точки от плана. В противен случай може да е обратният отговор.
Решението на частичните неравенства също използва интервалния метод. И планът за действие ще бъде:
- Използвайки описаните свойства, дайте на фракцията такъв вид, че остава само нула вдясно от знака.
- Заменете неравенството с "=" и определете точките, в които функцията ще бъде равна на нула.
- Маркирайте ги по координатната ос. В този случай числата, получени от изчисленията в знаменателя, винаги ще бъдат пробивани. Всички останали - въз основа на условията на неравенство.
- Определете интервалите на последователност.
- В отговор напишете обединението на тези интервали, чийто знак съответства на това, което е в първоначалното неравенство.
Ситуации, когато ирационалността се проявява в неравенството
С други думи, в записа има математически корен. Тъй като в училищния курс по алгебра повечето от задачите отиват за квадратен корен тогава ще бъде разгледано.
Решението на ирационалните неравенства е да се получи система от две или три, която ще бъде еквивалентна на оригинала.
| Оригинално неравенство | състояние | еквивалентна система |
| (N (x) <m (x) | m (x) е по-малко или равно на 0 | няма решения |
| m (x) по-голямо от 0 | n (x) е по-голямо или равно на 0 n (x) <(m (x)) 2 | |
| (N (x)> m (x) | m (x) е по-голямо или равно на 0 n (x)> (m (x)) 2 | |
или n (x) е по-голямо или равно на 0 m (x) е по-малко от 0 | ||
| (N (x) ≤ m (x) | m (x) е по-малко от 0 | няма решения |
| m (x) е по-голямо или равно на 0 | n (x) е по-голямо или равно на 0 n (x) ≤ (m (x)) 2 | |
| (N (x) ≥ m (x) | m (x) е по-голямо или равно на 0 n (x) ≥ (m (x)) 2 | |
или n (x) е по-голямо или равно на 0 m (x) е по-малко от 0 | ||
| (N (x) <(m (x) | n (x) е по-голямо или равно на 0 n (x) е по-малко от m (x) | |
| (N (x) * m (x) <0 | n (x) е по-голямо от 0 m (x) е по-малко от 0 | |
| (N (x) * m (x)> 0 | n (x) е по-голямо от 0 m (x) по-голямо от 0 | |
| (N (x) * m (x) ≤ 0 | n (x) е по-голямо от 0 m (x) ≤0 | |
или n (x) е 0 m (x) - всеки | ||
| (N (x) * m (x) ≥ 0 | n (x) е по-голямо от 0 m (x) ≥0 | |
или n (x) е 0 m (x) - всеки |
Примери за решаване на различни видове неравенства
За да добавим яснота към теорията за решаването на неравенствата, по-долу са примери.
Първи пример. 2x - 4> 1 + x
Решение: за да се определи TLD, е достатъчно само да се разгледа внимателно неравенството. Той се формира от линейни функции, затова се дефинира за всички стойности на променливата.
Сега от двете страни на неравенството трябва да се извади (1 + x). Оказва се: 2x - 4 - (1 + x)> 0. След като скобите са отворени и са дадени такива термини, неравенството приема следния вид: x - 5> 0.
Приравнявайки го на нула, лесно е да се намери неговото решение: x = 5.
Сега тази точка с номер 5, трябва да маркирате върху координатния лъч. След това проверете знаците на оригиналната функция. В първия интервал от минус безкрайност до 5, можете да вземете числото 0 и да го замените с неравенството, което е резултат от трансформациите. След изчисленията се оказва, че -7> 0. под дъгата на интервала трябва да подпишете знак минус.
На следващия интервал от 5 до безкрайност, можете да изберете числото 6. Тогава се оказва, че 1> 0. Под дъгата, знакът “+” е подписан. Този втори интервал ще бъде отговорът на неравенството.
Отговор: x лежи в интервала (5; ∞).
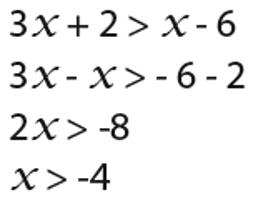
Вторият пример. Необходимо е да се реши система от две уравнения: 3x + 3 ≤ 2x + 1 и 3x - 2 ≤ 4x + 2.
Решението. LDL на тези неравенства също се намира в областта на всякакви числа, тъй като са дадени линейни функции.
Тогава трябва да действате поетапно. Първо конвертирайте първото от неравенствата и го приравнете към нула. 3x + 3 - 2x - 1 = 0. Това означава, че x + 2 = 0. Така x е -2.
Второто неравенство ще приеме формата на такова уравнение: 3x - 2 - 4x - 2 = 0. След трансформацията: -x - 4 = 0. Тя дава стойност за променливата, равна на -4.
Тези две числа трябва да бъдат маркирани на оста, изобразяващи интервалите. Тъй като неравенството не е строго, всички точки трябва да се оцветят. Първият интервал от минус безкрайност до -4. Нека номерът е -5. Първото неравенство ще даде стойност от -3, а второто, което означава, че тази разлика не е включена в отговора.
Вторият интервал е от -4 до -2. Можете да изберете номер -3 и да го замените и в двете неравенства. В първия и втория се получава стойността -1. Така че, под дъгата "-".
На последния интервал от -2 до безкрайност най-добрият брой е нула. Необходимо е да се замени и да се намерят стойностите на неравенствата. В първия от тях се получава положително число, а второто е нула. Тази разлика трябва също да бъде изключена от отговора.
От трите интервала решението на неравенството е само едно.
Отговор: x принадлежи на [-4; -2].

Третият пример. | 1 - x | > 2 | x - 1 |.
Решението. Първата стъпка е да се определят точките, в които функциите изчезват. За лявото това число ще бъде 2, за дясното - 1. те трябва да бъдат маркирани на лъча и да определят интервалите на знака на постоянството.
В първия интервал, от минус безкрайност до 1, функцията от лявата страна на неравенството приема положителни стойности, а от дясната страна приема отрицателни стойности. Под дъгата трябва да запишете двата знака "+" и "-" един до друг.
Следващият интервал е от 1 до 2. На него и двете функции приемат положителни стойности. Така че, под дъгата, две плюс.
Третият интервал от 2 до безкрайност дава следния резултат: лявата функция е отрицателна, а дясната - положителна.
Като се вземат предвид получените знаци, е необходимо да се изчислят стойностите на неравенството за всички интервали.
На първо място получаваме следното неравенство: 2 - x> - 2 (x - 1). Минусът преди двете във второто неравенство се дължи на факта, че тази функция е отрицателна.
След преобразуването неравенството изглежда така: x> 0. Той веднага дава стойностите на променливата. Това означава, че от този интервал ще се върне само интервалът от 0 до 1.
На второ: 2 - x> 2 (x - 1). Конверсиите ще дадат следното неравенство: -3x + 4 повече от нула. Неговата нула е x = 4/3. Като се вземе предвид знакът за неравенство, се оказва, че х трябва да бъде по-малък от този брой. Следователно този интервал се свежда до интервала от 1 до 4/3.
Последното дава следния запис на неравенството: - (2 - x)> 2 (x - 1). Нейната трансформация води до следното: x> 0. Това означава, че уравнението е вярно за х по-малко от нула. Това означава, че в изискваната празнина неравенството не дава решения.
В първите два интервала границата се оказва номер 1. Трябва да се провери отделно. Това означава, че замества първоначалното неравенство. Оказва се, че: | 2 - 1 | > 2 - 1 | Изчислението показва, че 1 е по-голямо от 0. Това е валидно изявление, така че единият е включен в отговора.
Отговор: x лежи в интервала (0; 4/3).