Обикновено и не толкова начини как да се изчисли коренът на куба

Колко гневни думи са изречени в неговия адрес? Понякога изглежда, че кубичният корен е невероятно различен от квадратния. Всъщност разликата не е толкова голяма. Особено ако разбирате, че те са само частни случаи на общия корен на n-та степен.

Но с неговото извличане може да възникнат проблеми. Но най-често те са свързани с тромави изчисления.

Какво трябва да знаете за корена на произволна степен?

Първо, дефинирането на това понятие. N-тият корен на някои "а" е такъв номер, който когато степенуване n дава оригинала "а".

Има и четни и нечетни градуси в корените. Ако п е равен, тогава радикалът може да бъде само нула или положително число. В противен случай няма да има реален отговор.

Когато степента е нечетна, тогава има решение за всяка стойност на "а". То може да е отрицателно.

Второ, коренната функция винаги може да бъде записана като степен, която е дроб. Понякога е много удобно.

Например, “а” към силата на 1 / n ще бъде точно коренът на n-тата сила на “а”. В този случай основата на степента винаги е по-голяма от нула.

По същия начин, “а” към мощността n / m ще бъде представен като корен на m-тата сила на “ ⁿ ”.

Трето, всички действия със степени са валидни за тях.

• Те могат да бъдат умножени. След това експонатите се събират.
• Корените могат да бъдат разделени. Степента ще трябва да бъде приспадната.
• И издигнете сила. Тогава те трябва да бъдат умножени. Това е степента, която е била, на тази, на която те строят.

Какви са приликите и разликите на квадратните и кубичните корени?

Те са подобни, като братята, само степента, в която имат, е различна. Принципът на изчисляването им е един и същ, единствената разлика е колко пъти трябва да се умножава числото, за да получи радикалния израз.

А за значителната разлика беше казано малко по-високо. Но повторете няма да е излишно. Квадратът се извлича само от неотрицателно число. Въпреки че е лесно да се изчисли кубически корен от отрицателна стойност.

Екстракция на кубичен корен на калкулатор

Всеки е правил това квадратен корен. А какво, ако степента на "3"?

На обикновен калкулатор има само бутон за квадрат, но кубичен не. Това ще помогне за простото изброяване на числа, които се умножават по три пъти. Да получиш радикален израз? Така че това е отговорът. Не работи? Вземи отново.

А какво да кажем за инженерната форма на калкулатор в компютър? Ура, има кубичен корен. Този бутон може просто да бъде натиснат и програмата ще даде отговор. Но това не е всичко. Тук можете да изчислите корена не само на 2 и 3 градуса, но и на произволно. Защото има бутон, в който степента на корена е "y". Това означава, че след натискане на този бутон, ще трябва да въведете друго число, което ще бъде равно на степента на корена, и едва след това "=".

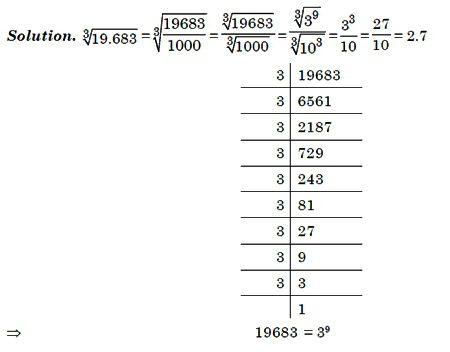
Ръчно извличане на корен от кубчета

Този метод е необходим, когато калкулаторът не е под ръка или не можете да го използвате. Тогава, за да се изчисли коренът на кубче от число, ще е необходимо усилие.

Първо, проверете дали пълният куб не е получен от някоя цяло число. Може би коренът е 2, 3, 5 или 10 в третата степен?

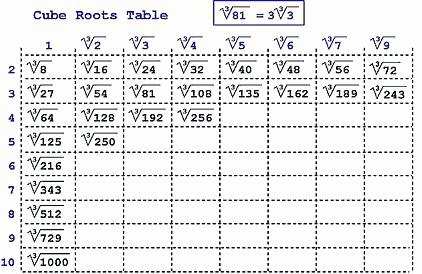
В противен случай ще трябва да се считате за колона. Алгоритъмът не е най-лесният. Но ако практикувате малко, действията ще бъдат лесно запомнени. Изчисляването на кубичния корен вече няма да бъде проблем.

1. Разделете радикалния израз на групи от три цифри от десетичната точка. Най-често е необходима дробната част. Ако не, трябва да завършите нули.
2. Определете броя, чийто куб е по-малък от целочислената част на радикалния израз. Напишете го в междинния отговор над знака корен. И под тази група да постави своя куб.
3. Направете изваждане.
4. Добавете първата група цифри към останалата част.
5. В черновата напишете израза: a ² * 300 * x + a * 30 * x ² + x ³ . Тук "а" е междинен отговор, "х" е число, което е по-малко от получения баланс с номера, присвоени му.
6. Номерът "x" трябва да бъде написан след запетая на междинния отговор. И стойността на целия израз да се запише под сравнения баланс.
7. Ако точността е достатъчна, тогава изчисленията спират. В противен случай трябва да се върнете към позиция 3.

Пример за изчисляване на кубичен корен

Това е необходимо, защото описанието може да изглежда сложно. Фигурата по-долу показва как да извлечете кубчевия корен от 15 до най-близката стотна.

Единствената трудност, която този метод има, е, че с всяка стъпка числата се увеличават много пъти и става по-трудно да се брои в бара.

1. 15> 2 ³ , след това под целочислената част 8 се записва и над корена 2.
2. След изваждане от 15 осем, получаваме остатъка от 7. Трябва да добавим три нули към него.
3. a = 2. Следователно: 2 ² * 300 * x + 2 * 30 * x ² + x ³ <7000, или 1200 x + 60 x ² + x ³ <7000.
4. Методът за подбор се оказва, че х = 4. 1200 * 4 + 60 * 16 + 64 = 5824.
5. Изваждането дава 1176 и числото 4 се появява над корена.
6. Задайте три нули на останалата част.
7. a = 24. Тогава 172800 x + 720 x ² + x ³ <1176000.
8. x = 6. Изчисляването на израза дава резултат 1062936. Баланс: 113064, над корена 6.
9. Присвояване на нули отново.
10. a = 246. Неравенството се получава, както следва: 18154800x + 7380x ² + x ³ <113064000.
11. x = 6. Изчисленията дават номера: 109194696, Баланс: 3869304. Над корена 6.

Отговорът е числото: 2, 466. Тъй като отговорът трябва да бъде даден на стотни, той трябва да бъде закръглен: 2.47.

Необичаен начин за извличане на кубичен корен

Може да се използва, когато отговорът е цяло число. Тогава кубичният корен се извлича чрез разлагане на радикана на нечетни термини. Освен това такива термини трябва да са минимално възможният брой.

Например, 8 е представено от сумата от 3 и 5. A 64 = 13 + 15 + 17 + 19.

Отговорът ще бъде число, което е равно на броя термини. Така кубичният корен от 8 ще бъде равен на два, а от 64 - четири.

Ако струва 1000 под корена, то декомпозирането му в термини ще бъде 91 + 109 + 93 + 107 + 95 + 105 + 97 + 103 + 99 + 101. Общо 10 термина. Това е отговорът.