Вероятност за събитие Определяне на вероятността за събитие

Първоначално, като просто събиране на информация и емпирични наблюдения на играта на зарове, теорията на вероятностите стана солидна наука. Първият, който й даде математическата рамка, бяха Ферма и Паскал.

От мислене за вечната до теория на вероятностите

Две личности, на които теорията на вероятността дължи много основни формули - Блез Паскал и Томас Байес, са известни като дълбоко религиозни хора, като последният е презвитериански свещеник. Очевидно желанието на тези двама учени да докажат заблудата на мнение за определено Фортуна, давайки късмет на домашните си любимци, даде тласък на научните изследвания в тази област. В края на краищата, всяка игра на късмета със своите печалби и загуби е само симфония на математически принципи.

Благодарение на вълнението на кавалера дьо Мере, който беше еднакво играч и човек, който не е безразличен към науката, Паскал беше принуден да намери начин да изчисли вероятността. De Mere се интересуваше от такъв въпрос: "Колко пъти трябва да хвърляте два зара на двойки, за да получите 12 точки повече от 50%?" Вторият въпрос, изключително се интересува от господин: "Как да разделим залога между участниците в незавършената игра?" Разбира се, Паскал успешно отговаря и на двата въпроса на де Мере, който става неволен инициатор на развитието на теорията на вероятността. Интересно е, че persona de Mere остава известна в тази област, а не в литературата.

Преди това нито един математик не е правил никакви опити за изчисляване на вероятностите на събитията, тъй като се е смятало, че това е само решение за предсказания. Блез Паскал даде първата дефиниция на вероятността от дадено събитие и показа, че това е конкретна фигура, която може да бъде доказана математически. Теорията на вероятностите стана основа за статистиката и се използва широко в съвременната наука.

Какво е инцидент

Ако разгледаме тест, който може да се повтори безкрайно много пъти, тогава можем да дефинираме случайно събитие. Това е един от вероятните резултати от експеримента.

Опитът е осъществяването на конкретни действия при непроменени условия.

За работа с резултатите от опита, събития обикновено се обозначават с буквите А, В, С, D, Е ...

Вероятност за случайно събитие

За да се пристъпи към математическата част на вероятността, е необходимо да се дефинират всички нейни компоненти.

Вероятността за дадено събитие е числово изразена мярка за възможността за възникване на дадено събитие (А или В) в резултат на опита. Показва вероятността като P (A) или P (B).

В теорията на вероятностите се различава:

• гарантирано е, че в резултат на експеримента P (=) = 1;
• невъзможно събитие никога не може да се случи P (Ø) = 0;
• случайно събитие се намира между надеждно и невъзможно, т.е. вероятността от неговото възникване е възможна, но не е гарантирана (вероятността за случайно събитие е винаги в рамките на 0≤P (A) ≤ 1).

Връзка между събития

Помислете и за едното, и за сумата от събития А + В, когато събитие се брои за изпълнението на поне един от компонентите, А или В, или и двете - А и В.

По отношение един на друг, събитията могат да бъдат:

• Равен на.
• Съвместим.
• Несъвместим.
• Противоположно (взаимно изключващо се).
• Зависим.

Ако две събития могат да се появят с еднаква вероятност, тогава те са еднакво възможни .

Ако възникването на събитие А не унищожи вероятността за възникване на събитие В, то те са съвместими.

Ако събития А и Б никога не се случват едновременно в едно и също преживяване, те се наричат несъвместими . Добър пример е хвърлянето на монета: появата на опашките е автоматично появата на орел.

Вероятността за сумата от такива несъвместими събития се състои от сумата на вероятностите за всяко от събитията:

Р (А + В) = Р (А) + Р (В)

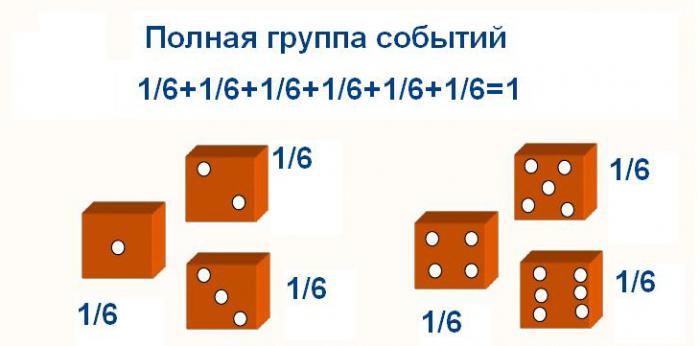
Ако възникването на едно събитие прави невъзможно да се случи друго, тогава те се наричат ​​противоположни. Тогава един от тях е обозначен като А, а другият - Ā (чете се като „не А“). Появата на събитие А означава, че Ā не се е случило. Тези две събития образуват пълна група със сума от вероятности, равна на 1.

Зависимите събития имат взаимно влияние, което намалява или увеличава вероятността един от друг.

Връзка между събития. примери

С примери е много по-лесно да се разберат принципите на теорията на вероятностите и комбинация от събития.

Опитът, който ще се извърши, е да извадите топките от кутията и резултатът от всяко преживяване е елементарен резултат.

Събитие е един от възможните резултати от опита - червена топка, синя топка, топка с номер шест и така нататък.

Номер на тест 1. Включени са 6 топки, три от които са оцветени в синьо, към тях се прилагат нечетни числа, а останалите три са червени с четни числа.

Тест номер 2. Има 6 сини топки с числа от един до шест.

Въз основа на този пример можете да извиквате комбинации:

• Надеждно събитие. На испански Събитие 2 “получи синята топка” е надеждно, тъй като вероятността за появата му е 1, тъй като всички топки са сини и не може да има пропуск. Докато събитието "получи топката с номер 1" - случайно.
• Невъзможно събитие. На испански №1 със сини и червени топки събитие "получи лилавата топка" е невъзможно, защото вероятността за появата му е 0.
• Равни събития. На испански Събитията от номер 1 „да вкараме топката с номер 2“ и „да вземем топката с номер 3“ са еднакво възможни, а събитията „вземете топката с четно число” и „получи топката с номер 2” имат различна вероятност.
• Съвместими събития. Два пъти поред, за да получите шест в процеса на хвърляне на умре - това са съвместими събития.
• Несъвместими събития. В същия изп. Събития №1 "получи червената топка" и "получи топката с нечетен брой" не могат да бъдат комбинирани в едно и също преживяване.
• Противоположни събития. Най-ярък пример за това е хвърлянето на монети, когато дърпането на орел е равносилно на не издърпване на опашки, а сумата на техните вероятности винаги е 1 (пълна група).
• Зависими събития . Така че, на испански. Номер 1 може да бъде настроен да извлече червената топка два пъти в ред. Неговото извличане или неизвличане за първи път влияе върху вероятността за екстракция за втори път.

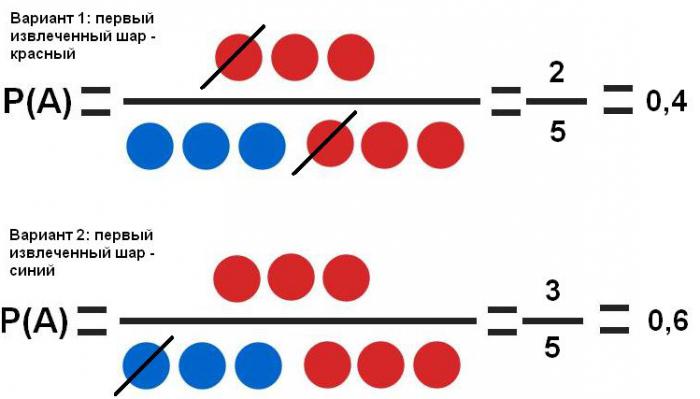
Вижда се, че първото събитие значително засяга вероятността от второто (40% и 60%).

Формула за вероятност на събитието

Преходът от предсказания към точни данни става чрез прехвърляне на темата към математическата равнина. Това означава, че преценките за случайно събитие като "висока вероятност" или "минимална вероятност" могат да бъдат преведени към конкретни цифрови данни. Такъв материал вече е допустим за оценка, сравнение и влизане в по-сложни изчисления.

От гледна точка на изчислението, определянето на вероятността за дадено събитие е съотношението на броя на елементарните положителни резултати към броя на всички възможни резултати от преживяването спрямо дадено събитие. Вероятността се обозначава с P (A), където P означава думата "probabilite", която се превежда от френски като "вероятност".

Така че формулата за вероятност за събитието:

P (A) = m / n,

Където m е броят на благоприятните резултати за събитие А, n е сумата от всички възможни резултати за този опит. В този случай вероятността за събитие винаги е между 0 и 1:

0 ≤ P (A) ≤ 1.

Изчисляване на вероятността за събитие. пример

Вземете sp. № 1 с топки, както е описано по-горе: 3 сини топки с номера 1/3/5 и 3 червени с числа 2/4/6.

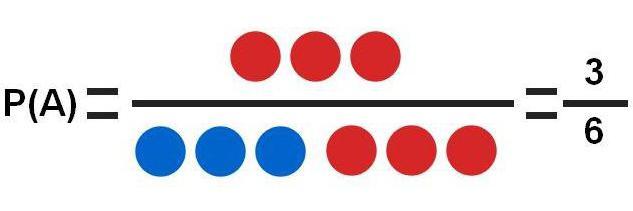
Въз основа на този тест могат да се разглеждат няколко различни задачи:

• А - загуба на червената топка. Има 3 червени топки и общо 6 опции.Това е най-простият пример, при който вероятността от събитие е P (A) = 3/6 = 0.5.
• Б - загуба на четен номер. Общият брой на четните числа е 3 (2,4,6), а общият брой възможни числени варианти е 6. Вероятността за това събитие е P (B) = 3/6 = 0.5.
• C - загуба на число, по-голямо от 2. Общо има 4 такива опции (3,4,5,6) от общия брой възможни резултати 6. Вероятността на събитието C е равна на P (C) = 4/6 = 0.67.

Както може да се види от изчисленията, случай С има по-голяма вероятност, тъй като броят на вероятните положителни резултати е по-висок, отколкото в А и В.

Несъответстващи събития

Такива събития не могат едновременно да се появят в едно и също преживяване. Както на испански № 1 е невъзможно едновременно да се получи синя и червена топка. Това означава, че можете да получите или синя, или червена топка. По същия начин, в заровете дори не може да се появи едновременно. нечетно число.

Вероятността от две събития се разглежда като вероятност за тяхната сума или продукт. Сборът от такива събития А + В се счита за такова събитие, което се състои в появата на събитие А или В и произведението на тяхното АБ - във външния вид на двете. Например, появата на две шест едновременно на лицата на две зарчета в една ролка.

Сумата от няколко събития е събитие, което включва появата на поне един от тях. Създаването на няколко събития е съвместна поява на всички тях.

В теорията на вероятността, като правило, използването на съюза "и" означава сума, съюз "или" - умножение. Формулите с примери ще помогнат да се разбере логиката на добавянето и умножението в теорията на вероятностите.

Вероятност за сумата от противоречиви събития

Ако се вземе предвид вероятността от несъвместими събития, вероятността за сумата от събития е равна на добавянето на техните вероятности:

Р (А + В) = Р (А) + Р (В)

Например: изчислете вероятността, че в sp. №1 със сини и червени топки ще падне числото между 1 и 4. Ние изчисляваме не в едно действие, а сумата на вероятностите на елементарните компоненти. Така че, в този опит, само 6 топки или 6 всички възможни резултати. Числата, които отговарят на условието, са 2 и 3. Вероятността за отпадане на 2 е 1/6, вероятността 3 също е 1/6. Вероятността да падне число между 1 и 4 е равна на:

1/6 + 1/6 = 1/3

Вероятността за сумата на несъвместимите събития от цялата група е 1.

Така че, ако в експеримента с куб се съберат вероятностите за отпадане на всички цифри, тогава като резултат получаваме едно.

Това е вярно и за противоположни събития, например в опита с монета, където едната страна е събитие А, а другата е обратното събитие, както е добре известно.

Р (А) + Р (Ā) = 1

Вероятност за създаване на несъвместими събития

Умножението на вероятностите се използва, когато се разглежда появата на две или повече несъвместими събития в едно наблюдение. Вероятността, че събития А и Б се появяват едновременно в нея, е равна на произведението на техните вероятности, или:

Р (А * В) = Р (А) * Р (В)

Например вероятността, че в sp. # 1 в резултат на два опита два пъти синя топка ще се появи, равна на

½ * ½ = ¼

Това означава, че вероятността от събитие, когато в резултат на два опита с извличане на топки само сини топки ще бъдат извлечени, е 25%. Много е лесно да се правят практически експерименти на тази задача и да се види дали това наистина е така.

Съвместни събития

Събитията се считат за съвместни, когато появата на една от тях може да съвпадне с появата на другата. Въпреки че са съвместни, се разглежда вероятността от независими събития. Например, хвърлянето на две зарчета може да даде резултат, когато цифрата 6 падне върху двете от тях.Въпреки че събитията съвпадат и се появяват по едно и също време, те са независими един от друг - само една шест може да падне, втората кост няма влияние върху нея.

Вероятността за съвместни събития се разглежда като вероятност за тяхната сума.

Вероятност за сумата от съвместни събития. пример

Вероятността за сума от събития А и В, които са съвместни, е равна на сумата от вероятностите на събитието минус вероятността за тяхната работа (т.е. тяхното съвместно изпълнение):

R _{съвместна.} (A + B) = P (A) + P (B) - P (AB)

Да приемем, че вероятността да уцелите целта с един изстрел е 0.4. Тогава събитие А - удари целта в първия опит, Б - във втория. Тези събития са съвместни, защото е възможно да ударите целта от първия и втория удар. Но събитията не са зависими. Каква е вероятността от възникване на събитие на поражение на целта с два изстрела (поне един)? Съгласно формулата:

0.4 + 0.4-0.4 * 0.4 = 0.64

Отговорът на въпроса е: "Вероятността да се удари в целта от два изстрела е 64%."

Тази формула за вероятността на дадено събитие може да се приложи и за несъвместими събития, където вероятността за съвместна поява на събитие P (AB) = 0. Това означава, че вероятността от сумата на несъвместимите събития може да се разглежда като особен случай на предложената формула.

Вероятностна геометрия за яснота

Интересното е, че вероятността от сумата на съвместните събития може да бъде представена под формата на две области А и В, които се пресичат помежду си. Както може да се види от картината, площта на тяхната асоциация е равна на общата площ минус областта на тяхното пресичане. Това геометрично обяснение прави формулата нелогична на пръв поглед по-разбираема. Забележете, че геометричните решения не са необичайни в теорията на вероятностите.

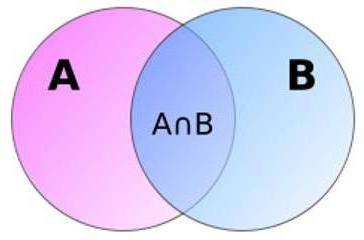
Определянето на вероятността от сумата на съвкупност (повече от две) от съвместни събития е доста тромаво. За да го изчислите, трябва да използвате формулите, които са предоставени за тези случаи.

Зависими събития

Зависимите събития се извикват, ако възникването на една (А) от тях влияе на вероятността за поява на друго (В). Освен това се взема предвид влиянието както на настъпването на събитие А, така и на неговото не-появяване. Въпреки че събития се наричат ​​зависими по дефиниция, само един от тях зависи (B). Обичайната вероятност се обозначава като P (B) или вероятността за независими събития. В случай на зависими се въвежда нова концепция - условната вероятност P _A (B), която е вероятността на зависимото събитие Б при условие, че е настъпило събитие А (хипотеза), от което зависи.

Събитие А също е случайно, следователно има вероятност, която трябва и може да бъде взета предвид при извършените изчисления. След това един пример ще покаже как да работим с зависими събития и хипотеза.

Пример за изчисляване на вероятността от зависими събития

Добър пример за изчисляване на зависими събития може да бъде стандартна карта от карти.

Използвайки примера на тесте от 36 карти, помислете за зависими събития. Необходимо е да се определи вероятността втората карта, извлечена от тестето, да бъде от костюма на диамантите, ако първата карта е:

1. Диамантите
2. Друг костюм.

Очевидно е, че вероятността за второто събитие Б зависи от първата А. Така че, ако първата опция е валидна, че в тестето е 1 карта (35) и 1 диамант (8) по-малко, вероятността за събитие Б:

РА (В) = 8/35 = 0.23

Ако втората опция е валидна, тогава има 35 карти в тестето, а пълният брой бутони (9) е запазен, след това вероятността за следващото събитие Б:

Р _A (В) = 9/35 = 0,26.

Може да се види, че ако събитие А е обусловено от факта, че първата карта е бубен, то вероятността на събитие В намалява и обратно.

Умножение на зависими събития

Водени от предишната глава, ние приемаме първото събитие (А) като факт, но ако говорим по същество, то е случайно. Вероятността за това събитие, а именно извличането на диаманти от тесте карти, е равна на:

Р (А) = 9/36 = 1/4

Тъй като теорията не съществува сама по себе си, но е предназначена да служи за практически цели, справедливо е да се отбележи, че вероятността за произвеждане на зависими събития е най-често необходима.

Според теоремата за произведението на вероятностите на зависими събития, вероятността за поява на съвместно зависими събития А и В е равна на вероятността едно събитие А да се умножи по условната вероятност на събитие В (в зависимост от А):

P (AB) = P (A) * P _A (B)

След това, в примера с тесте, вероятността за извличане на две карти с костюм от диаманти е:

9/36 * 8/35 = 0.0571, или 5.7%

А вероятността за извличане в началото не е тамбурините, а след това тамбурините са равни на:

27/36 * 9/35 = 0,19 или 19%

Може да се види, че вероятността за настъпване на събитие В е по-голяма, при условие че картата на костюма, различна от диамантите, първо се извлича. Този резултат е съвсем логичен и разбираем.

Обща вероятност за събитие

Когато проблем с условни вероятности стане многостранен, той не може да бъде изчислен с помощта на конвенционални методи. Когато има повече от две хипотези, а именно A1, A2, ..., A _n , .. формира пълна група от събития, при условие че:

• P (A _i )> 0, i = 1,2, ...
• A _i ∩ A _j = Ø, i ≠ j.
• _{K k} A _k = Ω.

Така че, формулата на общата вероятност за събитие Б с пълната група от случайни събития A1, A2, ..., A _n е равна на _:

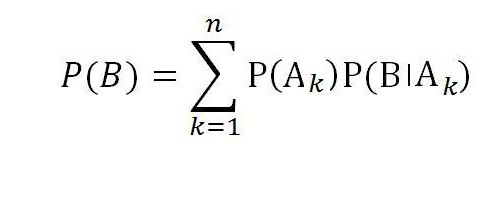
Поглед към бъдещето

Вероятността от случайно събитие е от съществено значение в много области на науката: иконометрия, статистика, физика и др. Тъй като някои процеси не могат да се определят детерминистично, тъй като самите те са вероятностни по своя характер, са необходими специални методи на работа. Теорията на вероятностите на дадено събитие може да се използва във всяко технологично поле като начин за определяне на възможността за грешка или неизправност.

Можем да кажем, че, признавайки вероятността, ние по някакъв начин правим теоретична стъпка в бъдещето, разглеждайки го през призмата на формули.