Момент на инерция: формула. Момент на инерция на тялото

За да се промени скоростта на движение на тялото в пространството, е необходимо да се положат известни усилия. Този факт се отнася за всички видове механични движения и е свързан с наличието на инерционни свойства на обекти с маса. В тази статия се разглежда ротацията на телата и се дава концепцията за техния момент на инерция.

Какво е ротация по отношение на физиката?

Отговорът на този въпрос може да даде на всеки, защото този физически процес не се различава от концепцията му в ежедневието. Процесът на въртене е движението на обект с крайна маса по кръгова пътека около някаква въображаема ос. Могат да се дадат следните примери за въртене:

• Движението на колелата на автомобила или велосипеда.
• Въртенето на ножовете на хеликоптер или вентилатор.
• Движението на нашата планета около оста и около слънцето.

Какви физически величини характеризират процеса на ротация?

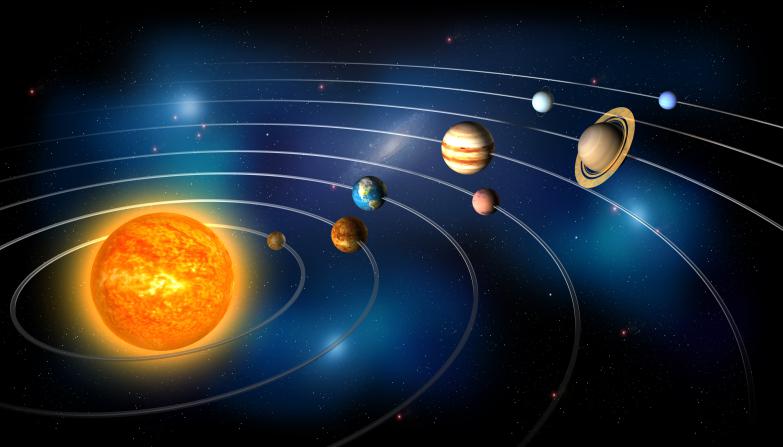
Кръговото движение се описва с набор от величини във физиката, основните от които са изброени по-долу:

• r е разстоянието до оста на материалната точка на масата m.
• ω и α са ъгловата скорост и ускорението, съответно. Първата стойност показва колко радиана (градуси) тялото се върти около оста за една секунда, втората стойност описва скоростта на промяна във времето на първата.
• L е ъгловият импулс, който е подобен на подобна характеристика при линейното движение.
• I - моментът на инерцията на тялото. Тази стойност е разгледана подробно по-долу.
• М е моментът на сила. Той характеризира степента на промяна в стойността на L, ако се приложи външна сила.

Тези величини са свързани помежду си със следните формули на въртеливо движение:

1. L = I * ω

2. M = I * a

Първата формула описва кръговите движения на тялото при отсъствие на действието на външните моменти на силите. В горната форма тя отразява закона за запазване на ъгловия момент L. Вторият израз описва случая на ускорение или забавяне на въртенето на тялото в резултат на действието на момента на сила М. И двата израза често се използват за решаване на проблемите на динамиката по кръгова пътека.

Както може да се види от тези формули, моментът на инерцията около оста (I) в тях се използва като определен коефициент. Нека разгледаме тази стойност по-подробно.

Откъде идва стойността на аз?

В този раздел ще разгледаме най-простия пример за въртене: кръгово движение на материална точка с маса m, чието разстояние от оста на въртене е r. Тази ситуация е показана на фигурата.

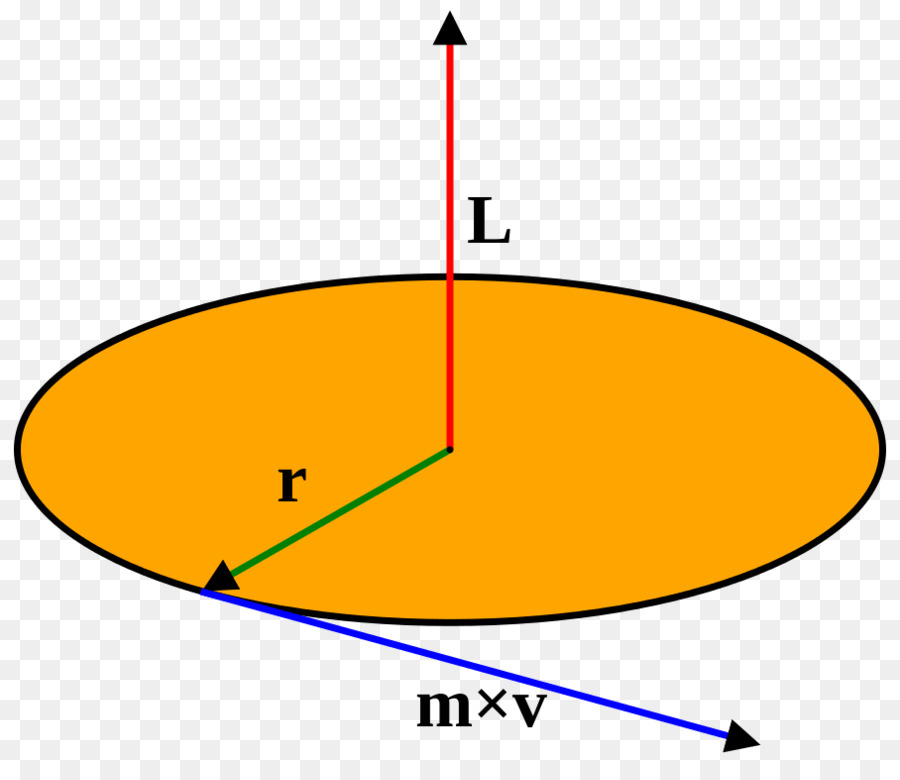
Според дефиницията, ъгловият момент L се записва като произведение на рамото r от линейните импулсни p точки:

L = r * p = r * m * v, тъй като p = m * v

Като се има предвид, че линейната и ъгловата скорост са свързани един с друг чрез разстоянието r, това равенство може да бъде пренаписано като:

v = ω * r => L = m * r ² * ω

Продуктът на масата на материална точка от квадрата на разстоянието до оста на въртене се нарича момент на инерция. Горната формула ще бъде пренаписана в този случай, както следва:

I = m * r ² => L = I * ω

Тоест, получихме израза, даден в предишния параграф, и въведохме стойността на I.

Общата формула за размер на тялото I

Изразът за момента на инерцията с маса m на материалната точка е базисен, т.е. позволява да се изчисли тази стойност за всяко тяло с произволна форма и неравномерно разпределение на масата в нея. За тази цел е необходимо да се раздели разглежданият обект на малки елементи от маса m _i (цяло число i е числото на елемента), след което всеки от тях да се умножи по квадрата на разстоянието r _i ² до оста, около която се разглежда въртенето, и да се добавят резултатите. Описаният метод за намиране на стойността на I може да бъде написан математически, както следва:

I = ( _i (m _i * r _i ² )

Ако тялото е разделено по такъв начин, че i-> ∞, тогава дадената сума се заменя с интеграл над масата на тялото m:

I = ( _m (r _i ² * dm)

Този интеграл е еквивалентен на друг интеграл върху обема на тялото V, защото dV = ρ * dm:

I = ρ * ( _V (r _i ² * dV)

И трите формули се използват за изчисляване на момента на инерцията на тялото. В този случай, в случай на дискретно разпределение на масата в системата, за предпочитане е да се използва 1-ви израз. При непрекъснато разпределение на масата се прилага третия израз.

Свойства на I и неговия физически смисъл

Описаната процедура за получаване на общ израз за I позволява да се направят някои изводи за свойствата на тази физическа величина:

• то е адитивно, т.е. общият момент на инерцията на системата може да бъде представен като сбор от моментите на отделните му части;
• тя зависи от разпределението на масата вътре в системата, както и от разстоянието до оста на въртене, колкото по-голямо е последното, толкова по-голямо I;
• тя не зависи от силите М, действащи върху системата от моменти, и от скоростта на въртене ω.

Физическият смисъл на I е как силно системата предотвратява всяка промяна в скоростта на въртене, т.е. моментът на инерция характеризира степента на "гладкост" на получените ускорения. Например колелото на велосипеда може лесно да се завърти до високи ъглови скорости и също така лесно да се спре, но за да се промени ротацията на маховика на коляновия вал на автомобила, ще са необходими значителни усилия и известно време. В първия случай има система с малък момент на инерция, във втория - с голям.

Стойността на I на някои тела за оста на въртене, преминаваща през центъра на масата

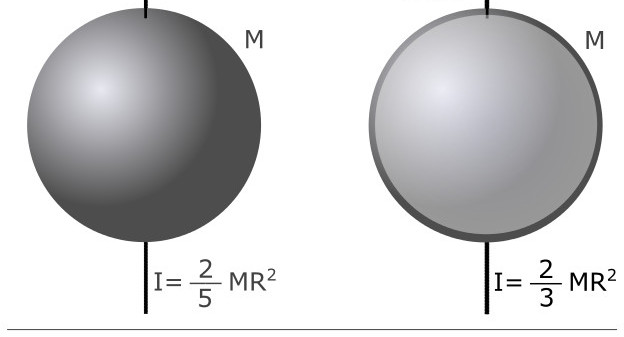
Ако приложим интеграция върху обема на всяко тяло с произволно масово разпределение, тогава можем да получим величината I. За хомогенни обекти, които имат идеална геометрична форма, този проблем вече е решен. Формулите за момента на инерцията на пръчка, диск и топка от маса m, в която съставната им материя е равномерно разпределена, са дадени по-долу:

• Ядрото. Оста на въртене работи перпендикулярно на него. I = m * L 2/12, където L е дължината на пръчката.
• Диск с произволна дебелина. Моментът на инерция с оста на въртене, преминаващ перпендикулярно на неговата равнина през центъра на масата, се изчислява, както следва: I = m * R 2/2, където R е радиусът на диска.
• Ball. С оглед на високата симетрия на тази цифра, за всяко положение на оста, минаваща през неговия център, I = 2/5 * m * R2, тук R е радиусът на топката.

По-долу са дадени два примера за решаване на задачи за прилагане на общата формула за изчисляване I и за използване на свойството на адитивност на това количество.

Задачата да се изчисли стойността на I за система с дискретно масово разпределение

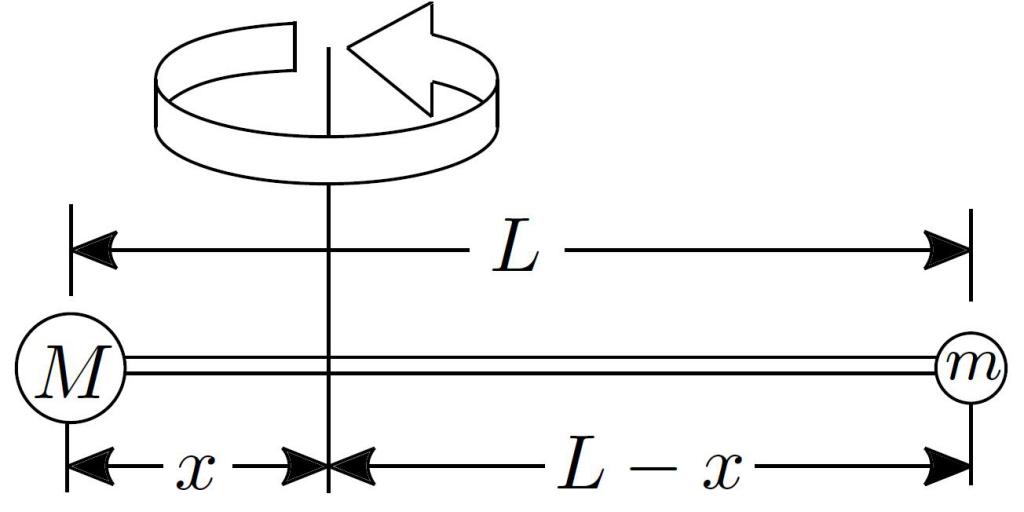
Представете си пръчка с дължина 0,5 метра, която е изработена от твърд и лек материал. Този прът е фиксиран по оста така, че да минава перпендикулярно на него точно по средата. На тази пръчка са окачени три тежести, както следва: от едната страна на оста са две тежести с тегло 2 kg и 3 kg, разположени съответно на разстояние 10 cm и 20 cm; от друга страна, еднократно тегло от 1,5 kg е окачено на края на пръта. За тази система е необходимо да се изчисли моментът на инерцията I и да се определи с каква скорост ω пръчката ще се върти, ако сила от 50 N бъде приложена към един от краищата й за 10 секунди.

Тъй като масата на пръта може да бъде пренебрегната, тогава е необходимо да се изчисли моментът I за всяко натоварване и да се добавят получените резултати, за да се получи пълният момент на системата. Според състоянието на задачата, от оста, теглото от 2 kg е на разстояние 0.15 m (0.25-0.1), натоварване от 3 kg е 0.05 m (0.25-0.20), натоварване от 1.5 kg е 0,25 м. Използвайки формулата за момента на I материалната точка, получаваме:

I = I ₁ + I ₂ + I ₃ = m ₁ * r ₁ ² + m ₂ * r ₂ ² + m ₃ * r ₃ ² = 2 * (0,15) ² + 3 * (0,05) ² + 1,5 * (0,25) ² = 0,14 625 kg * m ² .

Имайте предвид, че при извършване на изчисленията всички мерни единици са прехвърлени в системата SI.

За да се определи ъгловата скорост на въртене на пръчката след действието на силата, трябва да приложите формулата с момента на силата, която е дадена във втория параграф на статията:

M = I * a

Тъй като α = Δω / Δt и M = r * F, където r е дължината на рамото, получаваме:

r * F = I * Δω / Δt => Δω = r * F * Δt / I

Като се има предвид, че r = 0.25 m, заместваме числата във формулата, получаваме:

Δω = r * F * Δt / I = 0.25 * 50 * 10 / 0.14625 = 854.7 rad / s

Получената стойност е доста голяма. За да получите обичайната скорост, трябва да разделите Δω на 2 * pi радиана:

f = Δω / (2 xi) = 854.7 / (2 х 3.1416) = 136 s ^-1

Така приложената сила F до края на пръта с тежести за 10 секунди ще го завърти до честота от 136 оборота в секунда.

Изчисляването на стойността на I за пръчката, когато оста минава през неговия край

Нека да има хомогенен прът с маса m и дължина L. Необходимо е да се определи моментът на инерцията, ако оста на въртене е разположена в края на перпендикулярния му прът.

Използваме общия израз за I:

I = ρ * ( _V (r _i ² * dV)

Разрушавайки разглеждания обект в елементарни обеми, отбелязваме, че dV може да бъде записано като dr * S, където S е площта на напречното сечение на шината, а dr е дебелината на разделящия елемент. Подменяйки този израз във формулата, имаме:

I = ρ * S * ( _L (r ² * dr)

Този интеграл е много лесен за изчисляване, получаваме:

I = ρ * S * (r 3/3) ^L ₀ ^L => I = ρ * S * L 3/3

Тъй като обемът на пръта е S * L, а масата е ρ * S * L, тогава получаваме крайната формула:

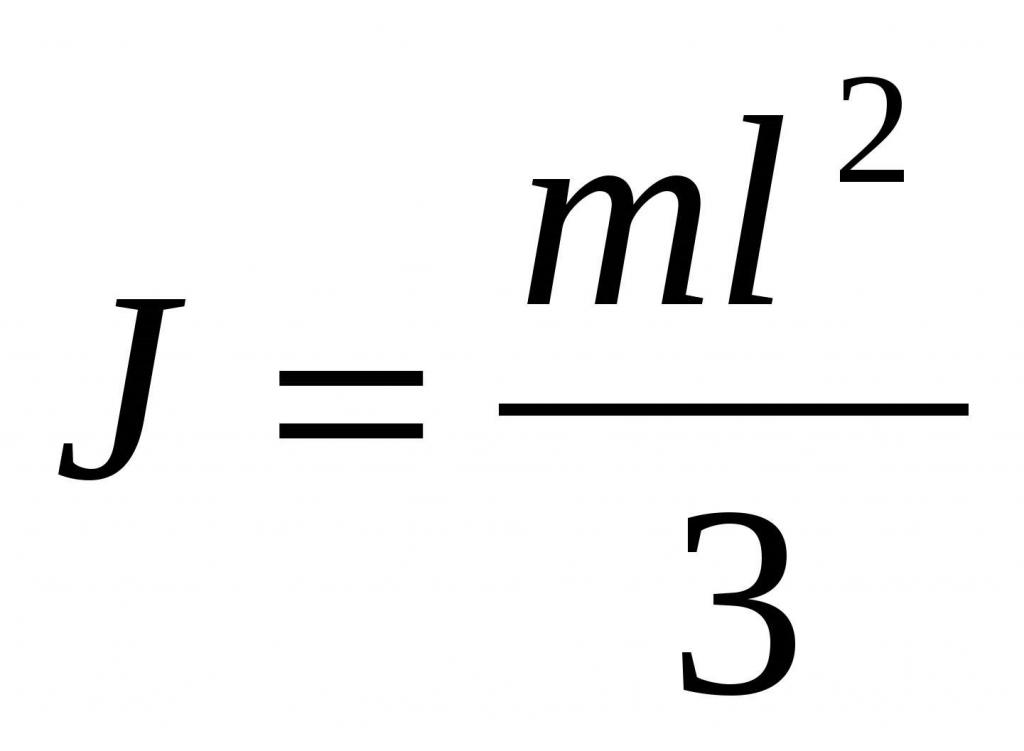
Интересно е да се отбележи, че моментът на инерция за същия прът, когато осът минава през неговия център на масата, е 4 пъти по-малък от получената стойност (m * L 2/3 / (m * L 2/12) = 4).