Как да намерим синуса на ъгъла

Синусът е една от основните тригонометрични функции, чието използване не се ограничава само до геометрията. Таблиците за изчисляване на тригонометричните функции, както и инженерните калкулатори, не винаги са под ръка, а понякога изчисляването на синуса е необходимо за решаване на различни проблеми. Като цяло, изчисляването на синуса ще спомогне за консолидиране на уменията за изготвяне и познаване на тригонометричните идентичности.

Игри с владетел и молив

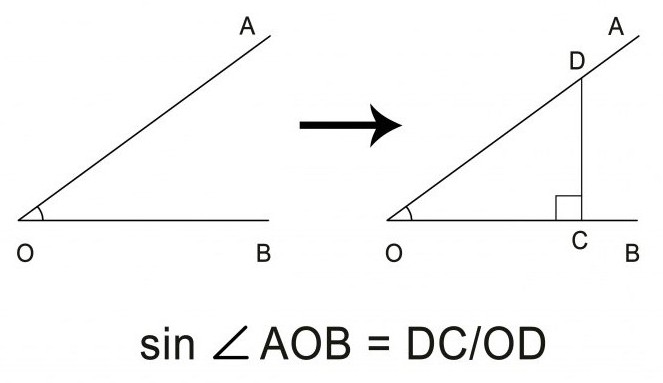
Една проста задача: как да намерим синуса на ъгъл, начертан на хартия? Ще ви е необходим стандартен владетел, триъгълник (или компас) и молив. Най-простият начин за изчисляване на синуса на ъгъла може да бъде чрез разделяне на далечния крак на триъгълника с прав ъгъл върху дългата страна - хипотенузата. Така първо трябва да добавите остър ъгъл към фигурата. правоъгълен триъгълник начертаване на линия, перпендикулярна на един от лъчите на произволно разстояние от върха на ъгъла. Необходимо е да се запази ъгъл точно 90 °, за което ще ни е необходим канцеларски триъгълник.

Използването на компас е малко по-точно, но отнема повече време. На една от гредите трябва да отбележите 2 точки на определено разстояние, да регулирате радиуса, приблизително равен на разстоянието между точките на компаса, и да начертаете полукръгове с центровете в тези точки, докато се получат пресечните точки на тези линии. Свързвайки точките на пресичане на нашите кръгове един с друг, получаваме строг перпендикуляр на лъча на нашия ъгъл, остава само да разширим линията до пресечната точка с друг лъч.

В получения триъгълник трябва да измерите с владетел страната, противоположна на ъгъла и дългата страна на един от лъчите. Съотношението на първото измерване към второто и ще бъде желаната стойност на синуса на острия ъгъл.

Намерете синуса за ъгъл, по-голям от 90 °

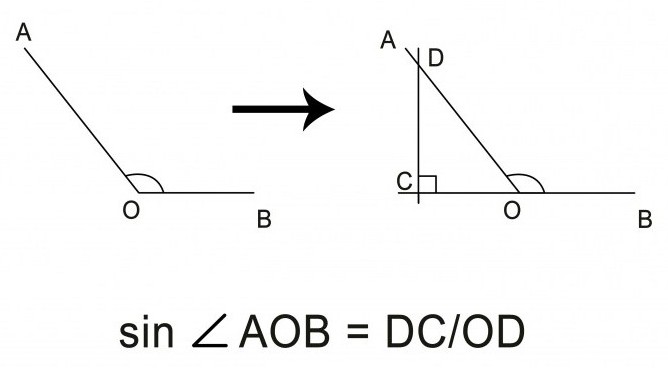
За тъп ъгъл задачата не е много по-трудна. Необходимо е да се начертае лъч от върха в обратна посока с помощта на линийка, за да се образува права линия с един от лъчите на интересуващия се ъгъл. С получения остър ъгъл трябва да се направи, както е описано по-горе, синусите на съседните ъгли, образуващи заедно разгънат ъгъл от 180 °, са равни.

Изчисляване на синуса за други тригонометрични функции

Също така е възможно синусовото изчисление, ако са известни стойностите на други тригонометрични функции на ъгъла или поне дължините на страните на триъгълника. Това ще ни помогне да използваме тригонометрични идентичности. Нека разгледаме общи примери.

Как да намерим синуса при познатия косинус на ъгъла? Първата тригонометрична идентичност, произтичаща от Питагоровата теорема, гласи, че сумата от квадратите на синуса и косинуса на същия ъгъл е равна на единица.

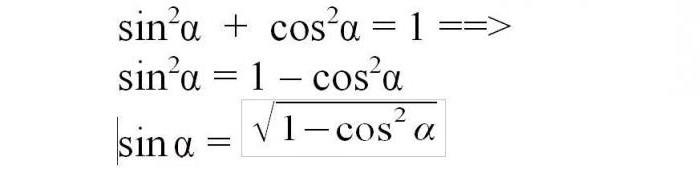
Как да намерим синуса при познатата допирателна на ъгъла? Допирателната се получава чрез разделяне на далечния крак от средата или разделянето на синуса от косинуса. Така, синусът е продукт на косинуса и на допирателната, а квадратът на синуса е квадратът на този продукт. Заменете косинуса в квадрата с разликата между единицата и квадратния синус според първата тригонометрична идентичност и чрез прости манипулации, даваме уравнението за изчисляване на квадратния синус чрез допирателната, съответно, за да изчислите синуса ще трябва да извлечете корена на резултата.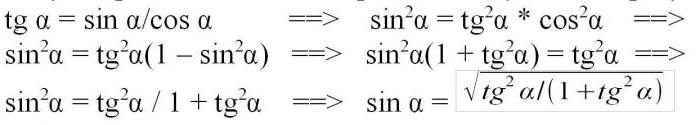

Как да намерим синуса при познатия ъгъл котангенс? Стойността на котангенса може да бъде изчислена чрез разделяне на дължината на близкия крак от ъгъла на крака на дълги разстояния и разделянето на косинуса от синуса, т.е. котангенсът е функцията, обратна на тангентата на числото 1. За да изчислим синуса, можете да изчислите допирателната с формулата tg α = 1 / ctg α и използвайте формулата във втората версия. Можете също да извлечете директна формула по аналогия с допирателната, която ще изглежда така.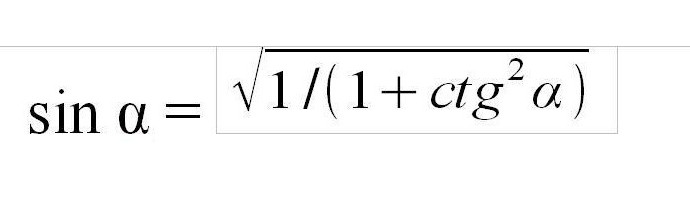

Как да намерим синуса от трите страни на триъгълника

Съществува формула за намиране на дължината на неизвестната страна на всеки триъгълник, не само правоъгълна, на две известни страни, като се използва тригонометричната косинусна функция на противоположния ъгъл. Изглежда така.

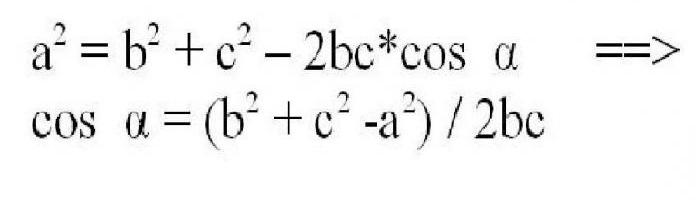Ами, синусът може да бъде допълнително изчислен от косинуса съгласно формулите по-горе.