Как да намерим областта на четириъгълника. Триъгълна зона

I. Предговор

Това е така, защото лош късмет: прекарали две седмици, дойдохте в училището и научихте, че сте пропуснали една много важна тема, задачите на която ще бъдат на изпитите в 9-ти клас - "Триъгълници, четириъгълници и тяхната област". Тук можете да бързате към учителя по геометрия с въпросите: "Как да намерим областта на четириъгълника?" Но половината от учениците се страхуват да се обърнат към учителите, така че те да не се считат за изоставащи, а втората половина се среща с учителите "помощ", подобно на "Погледни в учебника, там всичко е написано!" или "Не трябваше да пропускам уроците!" Но в учебника обикновено няма информация за правилата за намиране на областта на триъгълниците и четириъгълниците. И уроците бяха пропуснати за добра причина, има сертификат от лекаря. Но много учители се отказват от тези аргументи. Разбира се, те могат да бъдат разбрани: те не се плащат за допълнително качване на материала на урока в главите на учениците, които не разбират нищо. Много студенти изоставят този безполезен бизнес и се провалят за една година на изпита, като не успяват да получат дузина точки за задачата да открият областта на триъгълниците и четириъгълниците. И само няколко отиват в библиотеката и тези, които са запознати с въпроса: "Как да намерим площта на четириъгълника?" А различните хора и книги дават различни отговори и има голямо объркване на правилата. По-долу ще посоча основните начини за намиране на областите на триъгълниците и четириъгълниците.

II. четириъгълници

Да започнем с четириъгълници. В училищата и изпитите се разглеждат само изпъкнали четириъгълници, така че нека говорим за тях. Средно ниво на образование изследване на областите на паралелограми и трапеции. Паралелограмите идват в няколко форми: правоъгълник, квадрат, ромб и произволен паралелограм, в който се наблюдават само основните му характеристики: страните са успоредни и равни по двойки, сумата от съседни ъгли е 180 ^о . Но начините за намиране на областите на всички тези цифри са различни. Помислете за всеки отделно.

1. Правоъгълник

S на правоъгълника се дава по формулата: S = a * b, където а е хоризонталната страна, b е вертикалната страна.

2. Площ на квадратите

S на квадрата се намира по формулата: S = a * a, където a е страната на квадрата.

3. Квадратни диаманти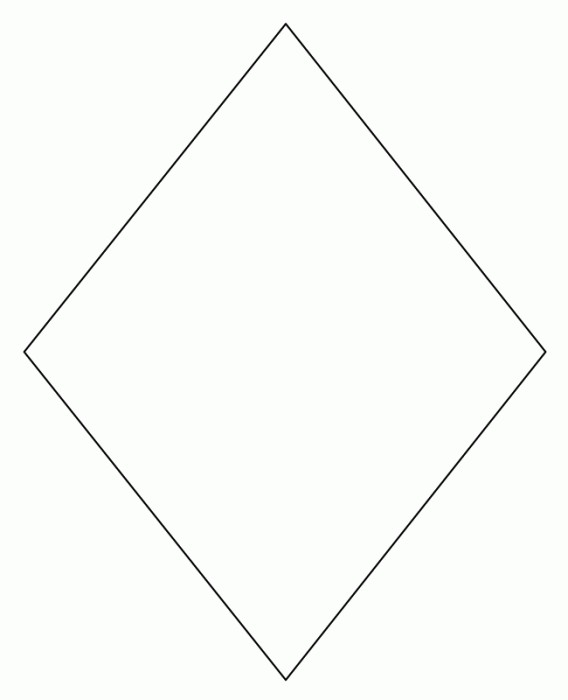

S ромб се намира по формулата: S = 0.5 * (d _{1 *} d ₂ ), където d ₁ е големият диагонален, ** d ₂ е по-малкият диагонал.

4. Областта на произволен паралелограм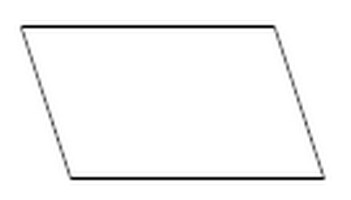

S на произволен паралелограм се намира по формулата: S = a * h _a , a е страната на успоредника, h _a е височината, насочена от тази страна.

Все още не всички?

С паралелограми сме свършили. - Трябва ли да научиш точно това? - облекчение, питаш. Отговарям: от паралелограми - да, точно това. Но все още има трапец и триъгълници. Така продължаваме.

III. стълба ация

Трапецовидна област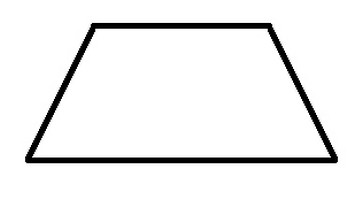

S трапеции могат да бъдат намерени с една формула, независимо дали е нормална или равнобедрена: S = ((a + b): 2) * h, където a, b са базисни ee, h ee височина. Това е всичко за трапеца. Сега на въпроса: "Как да намерим областта на четириъгълника?" - Можете не само да отговорите на себе си, но и да просветлите другите. Сега отидете на триъгълниците.

IV. триъгълник

В геометрията, за да се намери тяхната област, бяха изведени три формули: за правоъгълни, равностранни и произволни триъгълници.

1. Областта на триъгълника

S на произволен триъгълник се изчислява по формулата: S = 0.5a * h _a, a е страната на триъгълника, h _a е височината, изтеглена от тази страна.

2. Площ на равностранен триъгълник

S на равностранен триъгълник може да се намери по формулата: S = 0.5a * h, където а е основата на триъгълника, h е височината на този триъгълник.

3. Областта на десните триъгълници

област прави триъгълници се намира по формулата: S = (a * b): 2, където a е първият крак, b е вторият крак.

заключение

Е, това е, според мен, всичко. За триъгълници, също трябва да се научат малко, нали? Сега вижте всичко, което написах тук. "Кокосови дървета, за да научат това, ще отнеме месец!" - вероятно ви възкликва. И кой каза, че всичко се учи бързо? Но тогава, когато научите всичко това, няма да се страхувате от въпроси по темата "Как да намерите областта на четириъгълника" или "Областта на произволен триъгълник" на сертифицирането в 9-ти клас. Така че, ако искате да направите нещо, научете се, научете се и бъдете учен!

___________________________________

забележка

* - a и b не трябва да са на местата, които съм поставил. Когато решавате проблеми, можете да наричате вертикалната страна a и хоризонталната страна b;

** - диагоналите могат да се разменят и техните имена се променят точно както в бележката. *