Как да намерим областта на равнобедрен триъгълник?
Математиката е удивителна наука. Но такава мисъл идва само когато я разберете. За да постигнете това, трябва да решите проблеми и примери, да рисувате диаграми и рисунки, да докажете теореми.
Пътят към разбирането на геометрията е чрез решаване на проблеми. Отличен пример е задачата, в която трябва да намерите областта на равнобедрен триъгълник.
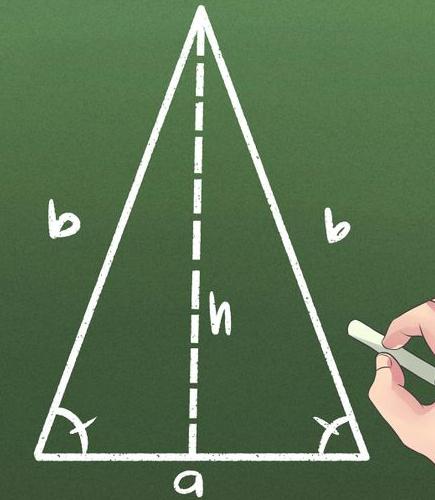
Какво е равнобедрен триъгълник и как е различен от другите?
За да не се страхувате от термините "височина", "зона", "база", "равнобедрен триъгълник" и други, ще трябва да започнете от теоретичните основи.
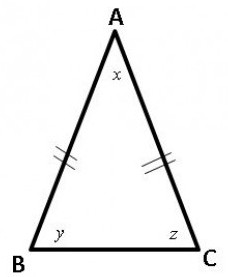
Първо за триъгълника. Това е плоска фигура, която се формира от три точки - върховете на свой ред, свързани чрез сегменти. Ако две от тях са еднакви, тогава триъгълникът става равнобедрен. Тези страни бяха наричани страни, а останалите станаха основа.
Ad
Има специален случай на равнобедрен триъгълник - равностранен, когато третата страна е равна на две странични.
Свойства на формата
Те се оказват верни помощници в решаването на проблеми, които изискват намирането на площ на равнобедрен триъгълник. Затова е необходимо да се познават и запомнят.
- Първият от тях: ъглите на равнобедрен триъгълник, от едната страна на който е основата, са винаги еднакви.
- Имуществото за допълнителни конструкции също е важно. Височините на неспарената страна, на медианата и на симетрията съвпадат.
- Тези сегменти, изтеглени от ъглите в основата на триъгълника, са двойки равни. Това твърде често улеснява намирането на решение.
- Две равни ъгли в него винаги имат значение по-малко от 90º.
- И накрая: изписаните и ограничени кръгове са конструирани така, че техните центрове се намират на височината на основата на триъгълника, което означава медиана и ситектор.

Как да разпознаем един равнобедрен триъгълник в проблем?
Ако при решаването на задачата възникне въпросът как да се намери площта на равнобедрен триъгълник, тогава първо трябва да разберете, че той принадлежи към тази група. И това ще помогне на определени знаци.
Ad
- Равни на два ъгъла или две страни на триъгълник.
- Бисекторът също е медиана.
- Височината на триъгълника е средната или симетрична.
- Равни на две височини, медиани или бисектриси на фигура.
Обозначения на количествата, приети във разглежданите формули
За да се опрости намирането на площта на равнобедрен триъгълник с помощта на формули, се въвежда подмяната на елементите й с букви.
| Буквата във формулата | име |
| и | фланг |
| в | дължина на основата |
| п | височина на основата |
| А | основен ъгъл |
| Най- | ъгълът между страните |
| общо наименование | област |
Внимание! Важно е да не се бърка "а" с "А" и "б" с "В". Това са различни количества.
Формули, които могат да бъдат използвани в различни задачи
Дължините на страните са известни и е необходимо да се намери площта на равнобедрен триъгълник.
В този случай трябва да се закръглят двете стойности. Числото, което е дошло от смяна на страна, умножете по 4 и извадете втората от нея. Извлечете от получената разлика квадратен корен. Дължината на основата се разделя на 4. Две числа се умножават. Ако напишете тези действия с букви, получавате следната формула:
Ad
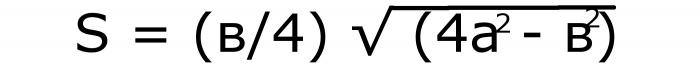
Да се запише под №1.
Намерете по стойностите на страните площта на равнобедрен триъгълник. Формула, която може да изглежда по-проста за някого от първата.
Първата стъпка е да намерим половината база. След това намерете сумата и разликата на този номер със страната. Умножете последните две стойности и извлечете квадратен корен. Последната стъпка е да се умножи всичко на половината база. Равенството на буквите ще изглежда така:
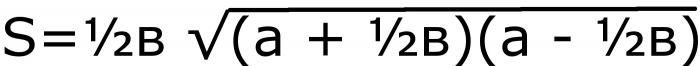
Това е формула номер 2.
Начин да се намери площта на равнобедрен триъгълник, ако основата и височината му са известни.
Една от най-кратките формули. Необходимо е да се умножат двете стойности на данните и да се разделят на 2. Ето как ще бъде написано:

Номерът на тази формула е 3.
В задачата са известни страните на триъгълника и ъгълът между основата и страната.
Тук, за да разберем каква ще е равнината на равнобедрен триъгълник, формулата ще се състои от няколко фактора. Първият от тях е стойността на синуса на ъгъла. Вторият е равен на произведението на страната към основата. Третият е част от ½. Обща математическа нотация:

Подредбата на формулата е 4.
В задачата са дадени: страната на равнобедрен триъгълник и ъгълът, разположен между страните му.
Както и в предишния случай, районът се намира на три фактора. Първият е равен на синуса на ъгъла, определен в условието. Вторият е квадратът на страната. А последното също е равно на половината от единицата. В резултат на това формулата се записва като:
Ad
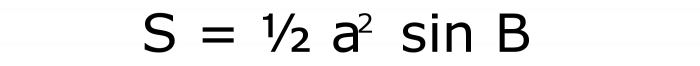
Номерът й е 5.
Формулата, която ви позволява да намерите областта на равнобедрен триъгълник, ако знаете неговата основа и ъгъла, разположен срещу него.
Първо трябва да изчислите допирателната от половината известен ъгъл. Умножете полученото число с 4. Завършете дължината на страната, която след това се дели на предишната стойност. Така получаваме следната формула:

Номерът на последната формула е 6.
Примери за задачи
Първа задача: известно е, че основата на равнобедрен триъгълник е 10 см, а височината му е 5 см. Необходимо е да се определи неговата площ.
За да го решим, логично е да се избере формула номер 3. В нея се знае всичко. Заместване на числа и броене. Оказва се, че площта е 10 * 5 / 2. Това е 25 см 2 .

Втората задача: в равнобедрен триъгълник са дадени страната и основата, които са съответно 5 и 8 cm.
Първият начин. Съгласно формулата номер 1. При подравняване на базата се получава числото 64, а четворното квадратче на страната е 100. След изваждане от второто, първото ще доведе до 36. Коренът е перфектно извлечен от него, който е 6. Базата е разделена на 4. и 6, което е 12. Това е отговорът: необходимата площ е 12 cm 2 .
Вторият начин. Съгласно формулата номер 2. Половината от основата е равна на 4. Сумата от страна и намереното число дава 9, разликата им е 1. След умножението получаваме 9. Премахването на квадратния корен дава 3. И последното действие, умножаващо 3 на 4, което дава същите 12 cm 2 .

Съвет: как да обичаме математиката
Решавайки проблеми в геометрията и определяйки как да намерим площта на равнобедрен триъгълник, можете да получите безценен опит. Колкото по-различни са възможностите за изпълнение на задачите, толкова по-лесно е да се намери отговор в нова ситуация. Следователно редовното и независимо изпълнение на всички задачи е пътят към успешното изучаване на материала.