Как да намерим областта на равностранен триъгълник: основни формули
Можете да намерите областта на равностранен триъгълник, като използвате произволна формула за произволна фигура от този тип или да използвате тези, които вече отчитат особеностите на тази фигура и математическите изрази са значително опростени.
Първият случай изисква само заместване на всички страни със същата стойност и като се има предвид, че всички ъгли на триъгълника са 60º. Тогава ще е необходимо да се извършат прости трансформации, които ще доведат до малко по-ниски формули, дадени в завършен вид.
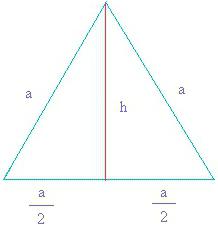
Формула 1: известна страна
В тази и следващите формули са приети стандартните обозначения за стойностите на триъгълника. Повече подробности могат да бъдат намерени в предложената таблица.
| стойност | Неговото обозначение |
| отстрани | и |
| област | S |
| височината | п |
| радиусите на изписаните и описани кръгове | r и R, съответно |
Изчисляването на площта на триъгълника в този случай ще се извърши по формулата:
S = /3 / 4 * a 2 .
Лесно се получава от това, което е известно за произволна фигура с три страни. Просто във формулата трябва да вземете предвид факта, че всички страни на триъгълника са равни.
По-точно се изисква формулата на Херона: S = √ (p (pa) (pb) (pc)). Стойността на полупериметъра за равностранен триъгълник ще бъде 3a / 2. Така, изразът ((3а / 2) - а) се получава във всяка скоба под корена. Тя ще даде след преобразуването на a / 2.
Тъй като има три скоби, тогава този израз ще има трета степен. Така ще се трансформира в 3/8.
Тя все още трябва да се умножи по полупериметър, който се дефинира като сумата на страните, разделена на 2. Получава се изразът: 3a 4/16. След екстракция квадратен корен просто изразът, даден в първата формула за областта на равностранен триъгълник, ще остане.
Следователно няма нужда да запомняте много формули. Можете просто да си спомните едно - Жирона. От него, чрез прости математически трансформации, всички останали се получават, например, за равностранен триъгълник.
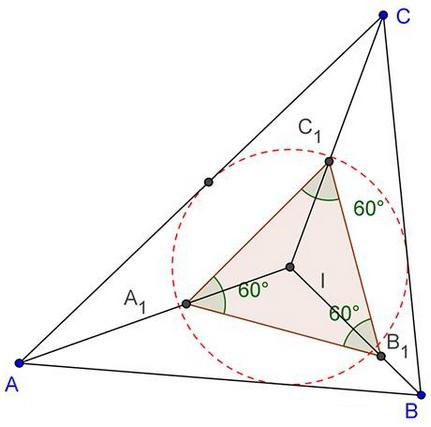
Формула 2: радиусът на вписания кръг
Този израз е много подобен на предишния запис. Но все още съществуват значителни различия: използва се друго писмо, ирационалността е стигнала до знаменателя, фактор 3 се е появил и номер 4 е изчезнал.
S = 3'3 * r2.
Тази формула също е лесно да се получи от това, дадено за произволен триъгълник. В него радиусът се умножава по сумата на страните и се разделя на 4. Тъй като страните имат една и съща стойност, сумата ще бъде заменена с 3а. Сега трябва да премахнете "а", за да остане само стойността на радиуса. Това ще изисква израз, при който страната е разделена от продукта 2 и синуса на противоположната страна на ъгъла. Тъй като ъгълът е 60º, стойността на синуса ще бъде /3 / 2. Тогава страната ще бъде изразена чрез радиуса, както следва: a = R3R. След проста трансформация, можете да стигнете до израза за областта, която е дадена в началото.
Формула 3: са описани кръгът и радиусът му
Тя е много подобна на първата. Само в числителя му се появява числото 3 и буквата се променя на R.
S = 3'3 / 4 * R2.
Тъй като радиусът е два пъти по-голям от този, разглеждан в предишния параграф, става ясно как се оказва. Той просто замества r с r / 2. И се извършват необходимите трансформации.
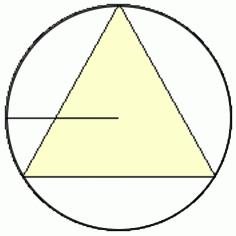
Следователно, формулата не може да бъде запомнена. Просто имайте предвид съотношението на вписаните радиуси и описани около равностранен триъгълник от кръгове.
Формула 4: известна височина
В този случай площта на равностранен триъгълник е:
S = n 2 / .3.
За да разберем как се получава тази формула, ще е необходимо отново да използваме общата за всички триъгълници. Прилича на произведението на страната и височината с ½. Сега, за да открием областта на равностранен триъгълник, е необходимо да си припомним или извлечем математически израз за височината.
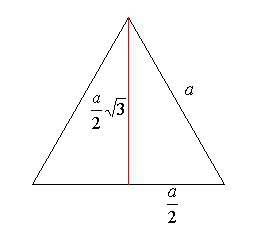
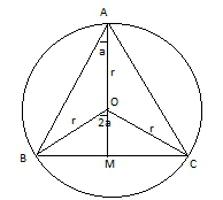
Лесно е да се научите, ако се възползвате от факта, че височината се формира правоъгълен триъгълник. Следователно височината може да се намери като крак - от Питагоровата теорема. Вторият крак ще бъде равен на половината от страната, тъй като височината също е средна (това е добре познато свойство на равностранен триъгълник). Тогава височината се определя като квадратен корен от разликата от два квадрата. Първият "а", а вторият "а / 2". След ерекцията във втора степен и извличането на корена остава: n = (/3 / 2) * a. От него a = 2n / .3. След като го заменим с основната формула за всички триъгълници, получаваме израза, посочен в началото на раздела.
Пример №1
Състояние. Изчислете площта на равностранен триъгълник, ако е известно, че неговата страна е 4 cm.
Решението. Тъй като стойността на страните на фигурата е известна, е необходимо да се използва първата формула.
Първо трябва да зачеркнете числото 4. От това действие получавате числото 16. Сега тя се намалява с четирите, стоящи в знаменателя. И в резултат 4 и remain3 остават в числителя, а знаменателят става равен на единица, което означава, че просто не може да бъде записан. Това е резултатът, който се изисква да се намери в проблема.
Отговор: 4,3 см 2 .
Пример 2
Състояние. Всички страни на равностранен триъгълник са равни на 2√2 dm. Изчислете площта му.
Решението. Аргументите са същите като при първата задача. Само стойността на страничния квадрат ще бъде различна. Трябва да се вгради отделно втора степен 2 и ирационалност. Резултатът ще бъде следният: 4 * 2 = 8. След редукцията с знаменателя, 2 и remain3 остават в числителя на фракцията и знаменателят изчезва.
Отговор: 2√3 dm 2 .
Пример номер 3
Състояние. Кръг е вписан в равностранен триъгълник, радиусът му е 2,5 см. Необходимо е да се изчисли площта на триъгълника.
Решението. За да изчислите желаната стойност, трябва да използвате втората формула.
Първо, стойността на радиуса трябва да бъде на квадрат. Оказва се, че 6.25. Тогава тази стойност трябва да се умножи по 3. Резултатът от това действие ще бъде числото 18.75. Но това не е крайната стойност: тя ще има коефициент ,3, който присъства в използваната формула.
Отговорът: 18.75√3 cm 2 .
Пример 4
Състояние. Необходимо е да се определи коя площ на равностранен триъгълник е равна, ако е известна нейната височина - 3 dm.
Решението. Естествено, трябва да изберете четвъртата формула. С негова помощ най-лесният начин да намерите отговор на този проблем.
Достатъчно е просто да се сдвои числото 3, т.е. височината, която ще даде стойността 9. И след това да се раздели на ,3, стояща във формулата.
Тъй като в математиката не е обичайно да се оставя ирационалност в знаменателя на отговора, трябва да се отървете от него. За да направите това, фракцията 9/3 ще трябва да бъде умножена с фракцията със същия числител и знаменател, а именно /3 / .3. От това действие стойността 9√3 се появява в числителя и числото 3 се появява в знаменателя.
Тази част Това може да бъде намалено с 3. Това е крайният резултат.
Отговор: площта е 3√3 dm 2 .
Пример номер 5
Състояние. Даден е равностранен триъгълник с площ от 27 cm2. С тази стойност трябва да знаете дължината на страната на фигурата.
Решението. Тъй като това е за страната, първата формула ще направи. От него можете веднага да извлечете математически израз, който ви позволява да определите страната на триъгълника.
За да направите това, площта трябва да се умножи по 4 и да се раздели на квадратен корен от три. Затова вземете стойността на страната на площада. За да получите само страна, трябва да извлечете корена. Изразът за страната ще изглежда така: a = 2 * √ (S / )3).
Тъй като областта е известна, можете незабавно да продължите с изчисленията. Радикален израз изглежда като коефициент 27 и 3. Необходимо е да се отървете от ирационалността в знаменателя. Оказва се, че е 27√3, разделен на 3. След редукцията 1 остава в знаменателя, който не можете да напишете, а 9√3 остава в числителя.
Следващата стъпка е да извлечете корена от получения израз. Първият фактор дава стойност 3. Но второто, ,3, изисква внимание. За да се опрости задачата, можете да извлечете тези корени и да закръглите стойностите.
3 = 1,73; сега извличаме отново корена от него и получаваме 1.32.
Остава само да го умножите по 2 и да получите желания резултат.
Отговор: страната е равна на 2.64 cm.