Как да намерим диамантен квадрат? Възможни начини за намиране на отговор

Математиката е учебен предмет, който се изучава от всички, независимо от профила на класа. Въпреки това, тя не е обичана от всички. Понякога несправедливо. Тази наука постоянно хвърля на учениците задачи, които позволяват на мозъка им да се развива. Математиката се справя с, за да не дава на децата умствени способности да избледняват. Една от частите му се справя с това особено добре - геометрията.

Всяка от темите, които се изучават в нея, заслужава внимание и уважение. Геометрията е начин да се развие пространствено въображение. Пример за това е темата за квадратите на фигурите, по-специално диамантите. Тези пъзели могат да доведат до задънена улица, ако не разбирате подробностите. Защото са възможни различни подходи за намиране на отговор. Някой по-лесно си спомня различни версии на формулите, които са написани по-долу, и някой е в състояние да ги извлече от предварително научения материал. Във всеки случай, безнадеждни ситуации не се случват. Ако мислите малко, решението със сигурност ще бъде намерено.

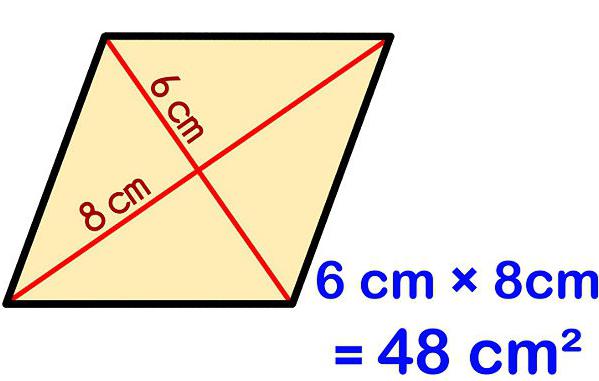
Какво е ромб и как изглежда като други четириъгълници?

Отговорете на този въпрос, за да разберете принципите за получаване на формули и хода на разсъжденията в проблемите. В края на краищата, за да разберете как да намерите област ромб, трябва ясно да разберете каква е цифрата и какви са нейните свойства.

За удобство при разглеждането на успоредник, който е четириъгълник с двойни паралелни страни, ще вземем "родителя". Той има две "деца": правоъгълник и ромб. И двете са успоредни. Ако продължим паралелите, това е "фамилното име". Така че, за да намерим ромб Можете да използвате вече изучената формула на паралелограма.

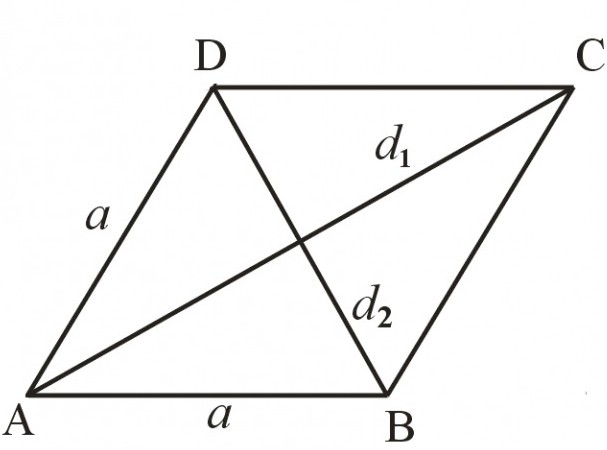
Но, както всички деца, ромбът има нещо свое. Това е малко по-различно от "родителското" и може да се разглежда като отделна цифра. В края на краищата, правоъгълникът не е ромб. Връщайки се към паралелите - те са като брат и сестра. Те имат много общи неща, но те все още се различават. Тези различия са техните специални свойства, които трябва да се използват. Би било странно да се знае за тях и да не се прилага при решаването на проблеми.

Ако продължим аналогията и запомним друга фигура - квадрат, то тя ще бъде продължение на ромб и правоъгълник. Тази цифра съчетава всички свойства на едното и на другото.

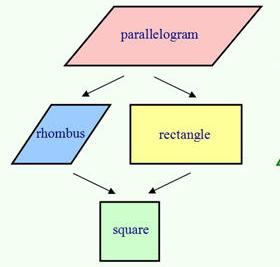
Диамантени свойства

Има пет от тях и те са изброени по-долу. А някои от тях повтарят свойствата на паралелограма, а някои са присъщи само на разглежданата фигура.

• Ромб е успоредник, който е придобил специална форма. От това следва, че неговите страни са двойки паралелни и равни. Нещо повече, те са неравномерни по двойки и това е всичко. Както щеше да има квадрат.
• Диагоналите на този четириъгълник се пресичат под ъгъл, равен на 90º. Това е удобно и значително опростява хода на разсъжденията при решаване на проблеми.
• Друго свойство на диагоналите: всяка една от тях се разделя на точка на пресичане на равни сегменти.
• Ъглите, разположени една срещу друга, са равни.
• И последното свойство: диагоналът на ромба съвпада с бисектрисите на ъглите.

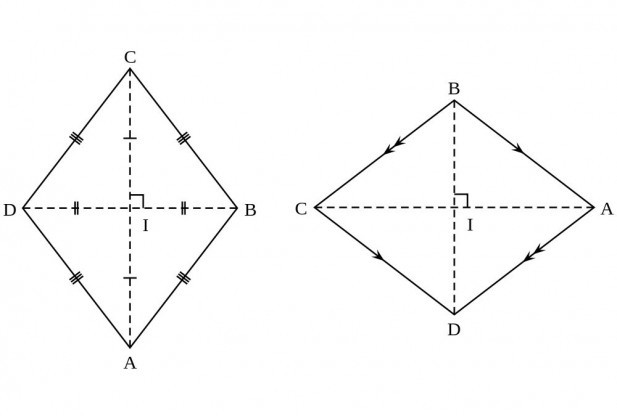
Обозначения, които са приети във разглежданите формули

В математиката е необходимо да се решават проблеми, като се използват общи буквени изрази, които се наричат ​​формули. Темата на площада не е изключение.

За да отидете на записите, които разказват как да намерите областта на диаманта, трябва да се съгласите с буквите, които заменят всички цифрови стойности на елементите на фигурата.

Сега е време да напишем формулите.

Сред данните за задачите има само диагонални диаманти.

Правилото гласи, че за да се намери неизвестно количество, трябва да се умножат дължините на диагоналите и след това да се раздели продукта на половина. Резултатът от разделянето е областта на ромба в диагоналите.

Формулата за този случай ще изглежда така:

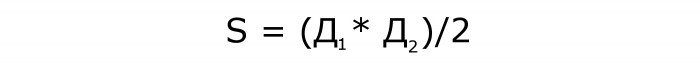
Нека тази формула отиде на номер 1.

Задачата е дадена страна на диаманта и неговата височина

За да изчислите площта, трябва да намерите продукта от тези две количества. Може би това е най-простата формула. Освен това е известно от темата за областта на успоредника. Там такава формула вече е проучена.

Математическо писане:

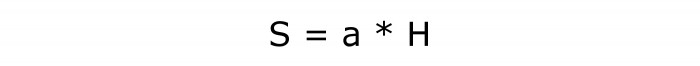
Номерът на тази формула е 2.

Известен страничен и остър ъгъл

В този случай, трябва да направите квадрат на размера на ромбовата страна. След това намерете синуса на ъгъла. Третата стъпка е да се изчисли произведението на двете формирани количества. Отговорът ще бъде диамантеният квадрат.

Буквален израз:

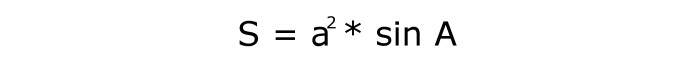
Серийният му номер е 3.

Тези стойности: радиусът на вписаната окръжност и остър ъгъл

За да изчислите площта на ромб, трябва да намерите квадрата на радиуса и да го умножите по 4. Определете стойността на синуса на ъгъла. След това разделете продукта на второто количество.

Формулата приема следната форма:

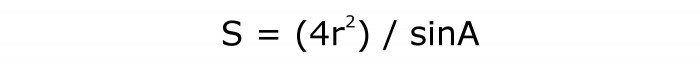
Той ще бъде номериран 4.

Проблемът включва страната и радиуса на вписания кръг.

За да определите как да намерите областта на ромб, трябва да изчислите произведението на тези количества и числото 2.

Формулата за тази задача ще изглежда така:

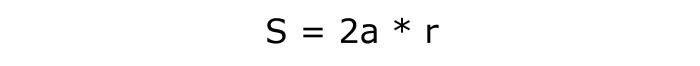
Номерът й е в ред - 5.

Примери за възможни задачи

Задача 1

Един от диагоналите на ромба е 8, а другият е 14 см. Необходимо е да се намери площта на фигурата и дължината на неговата страна.

решение

За да намерите първата стойност, се нуждаете от формула 1, в която D ₁ = 8, D ₂ = 14. След това площта се изчислява, както следва: (8 * 14) / 2 = 56 (cm ² ).

Диагоналите разделят диаманта на 4 триъгълника. Всеки от тях ще бъде правоъгълен. Това трябва да се използва за определяне на стойността на второто неизвестно. Страната на ромба ще стане хипотенузата на триъгълника, а краката ще бъдат половината от диагоналите.

Тогава a ² = (D _1/2 ) ² + (D 2/2) ^2. След като заменим всички стойности, получаваме: a ² = (8/2) ² + (14/2) ² = 16 + 49 = 65. Но това е квадратът на страната. Така че трябва да извлечете квадратен корен След това страничната дължина ще бъде приблизително равна на 8,06 cm.

Отговор: площта е 56 см ² , а страната е 8.06 см.

Задача 2

Диамантената страна е със стойност 5.5 dm, а височината му е 3.5 dm. Намерете областта на фигурата.

решение

За да се намери отговорът, е необходима формула 2. В нея, a = 5.5, H = 3.5. След това, замествайки буквите във формулата с числа, получаваме, че желаната стойност е 5.5 * 3.5 = 19.25 (dm ² ).

Отговор: областта ромб е равна на 19,25 dm ² .

Задача 3

Острият ъгъл на ромба е 60º, а по-малкият му диагонал е 12 см. Необходимо е да се изчисли площта му.

решение

За да получите резултата, ще ви е нужна формула номер 3. В нея вместо А ще има 60, а стойността на a е неизвестна.

За да намерите страната на ромб, трябва да си припомните теоремата за синуса. В правоъгълен триъгълник, a ще бъде хипотенуза, по-малкият крак е равен на половината от диагонала, а ъгълът е разделен наполовина (известен от имота, където се споменава бисектъра).

Тогава страната а ще бъде равна на произведението на крака в синуса на ъгъла.

Краката трябва да бъде изчислена като D / 2 = 12/2 = 6 (cm). Синус (A / 2) ще бъде равен на стойността му за ъгъл от 30º, т.е. 1/2.

Чрез извършване на прости изчисления получаваме следната стойност на ромбовата страна: a = 3 (cm).

Сега площта е продукт на 3 ² и синус 60 °, т.е. 9 * (√3) / 2 = (9√3) / 2 (cm2).

Отговор: желаната стойност е (9√3) / 2 cm2.

Резултати: всичко е възможно

Тук бяха разгледани някои възможности за намиране на областта на диаманта. Ако не е ясно в проблема директно коя формула да се използва, тогава трябва да помислите малко и да се опитате да свържете предварително проучените теми. В други теми винаги има намек, който ще помогне да се свържат известните стойности с тези във формулите. И проблемът ще бъде решен. Най-важното е да се помни, че всичко, което преди това се изучава, може и трябва да се използва.

В допълнение към предложените задачи са възможни и обратни задачи, когато площта на фигурата трябва да изчисли стойността на даден диамантен елемент. След това трябва да използвате уравнението, което е най-близо до състоянието. След това конвертирайте формулата, оставяйки неизвестна стойност от лявата страна на равенството.