Как да се изчисли диагоналът на призмата на прав четириъгълник?

Призма е геометрична обемна фигура, чиито характеристики и свойства се изучават във висшите училища. Като правило, при изучаването му, се вземат предвид количествата като обем и площ. В тази статия ще отворим малко по-различен въпрос: даваме метод за определяне на дължината на призматичните диагонали по примера с четириъгълна форма.

Каква цифра се нарича призма?

В геометрията е дадена следната дефиниция на призмата: тя е триизмерна форма, ограничена от две многоъгълни идентични страни, които са успоредни една на друга, и от няколко паралелограми. Фигурата по-долу показва пример на призма, която отговаря на това определение.

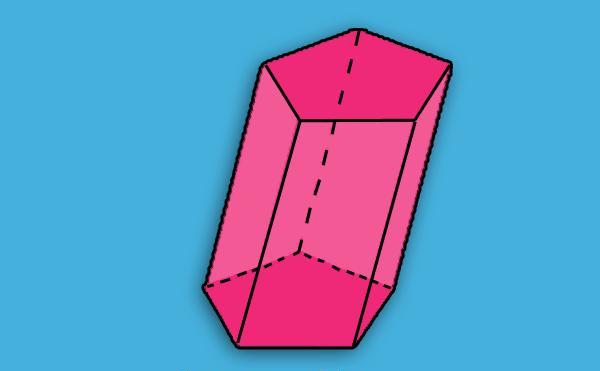
Виждаме, че два червени петоъгълника са еднакви и са в две паралелни равнини. Пет розови паралелограма свързват тези петоъгълници в един обект - призма. Две петоъгълници се наричат ​​основи на фигурата, а паралелограмите - странични.

Призмите са прави и наклонени, които също се наричат ​​правоъгълни и наклонени. Разликата между тях е в ъглите между основата и страничните повърхности. За правоъгълна призма всички тези ъгли са 90 ^° .

Според броя на страните или върховете на полигона в основата, те говорят за призми триъгълни, петоъгълни, четириъгълни и т.н. И ако този многоъгълник е правилен, а самата призма е права линия, тогава такава форма се нарича правилна.

Призмата, показана на предишната фигура, е петоъгълна. По-долу е направена петоъгълна права призма.

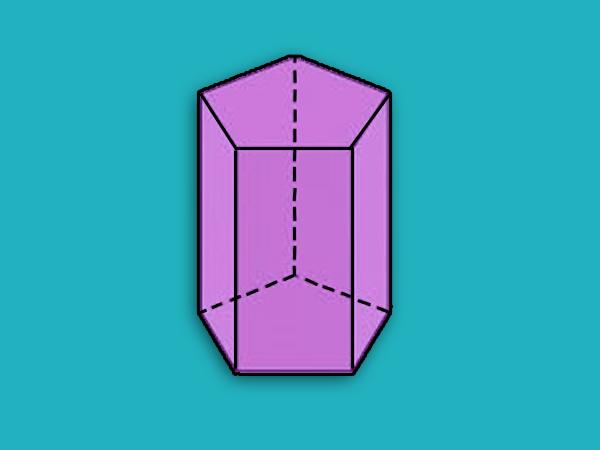
Всички изчисления, включително методът за определяне на диагонала на призмата, е удобно да се изпълняват точно за точните цифри.

Какви елементи характеризират призмата?

Елементите на фигурата са съставните им части. Специално за призмата има три основни типа елементи:

• върхове;
• лица или страни;
• ребрата.

Лицата са базите и страничните равнини, които представляват паралелограми в общия случай. В призмата всяка страна винаги е от един от двата вида: или полигон, или успоредник.

Ръбовете на призмата са тези сегменти, които ограничават всяка страна на фигурата. Подобно на ръбовете, ръбовете са също от два вида: принадлежащи към основата и страничната повърхност или принадлежащи само на страничната повърхност. Първият винаги е два пъти по-голям от втория, независимо от вида на призмата.

Върховете са точките на пресичане на трите ръба на призмата, две от които лежат в равнината на основата, а третата принадлежи на две странични повърхности. Всички върхове на призмата са в равнините на основата на фигурата.

Номерата на описаните елементи са свързани в едно равенство, което има следната форма:

Р = В + С-2.

Тук P е броят на ръбовете, B - върховете, C - страните. Това равенство се нарича теорема на Ойлер за полиедър.

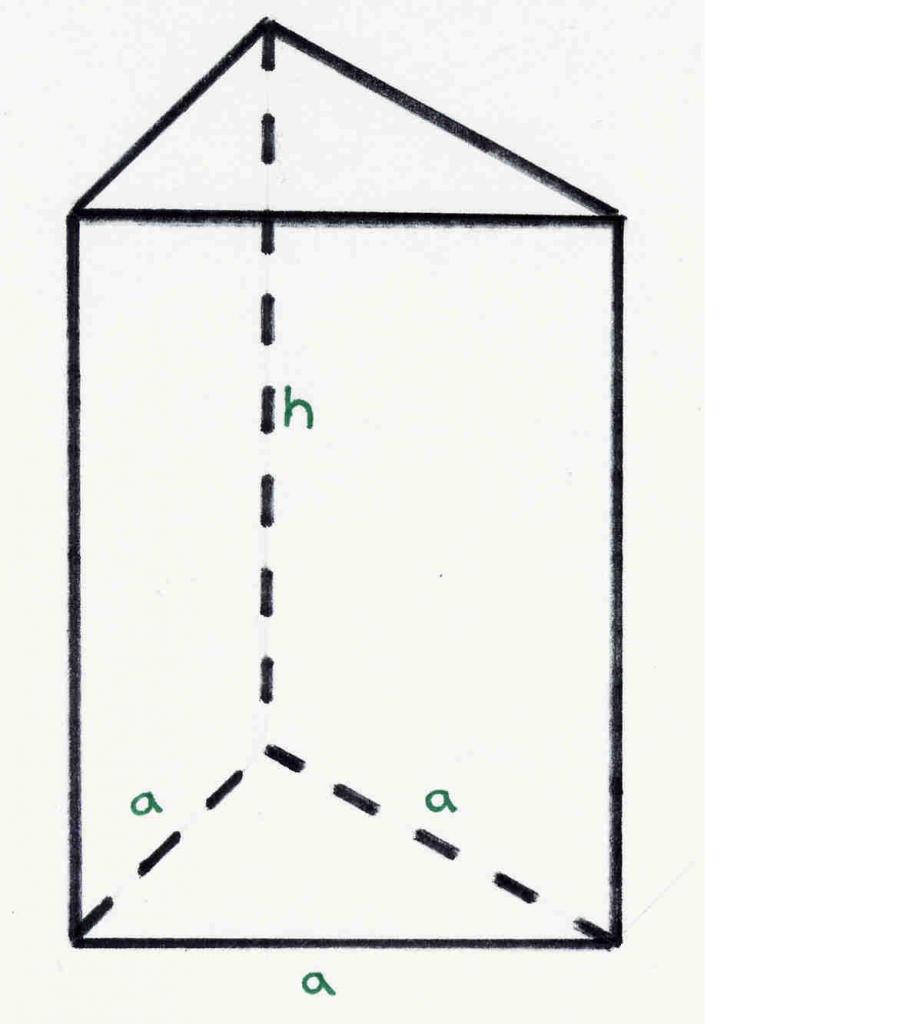
Фигурата показва правилна триъгълна призма. Всеки може да открие, че има 6 върха, 5 страни и 9 ръба. Тези числа съответстват на теоремата на Ойлер.

Диагонални призми

След като свойства като обем и площ, при проблеми в геометрията, често се открива информация за дължината на даден диагонал на разглежданата фигура, която или се дава, или се налага, като се използват други известни параметри. Помислете какъв е диагоналът на призмата.

Всички диагонали могат да бъдат разделени на два типа:

1. Лежи в равнината на лицата. Те свързват несъседните върхове на полигона в основата на призмата или на паралелограмата на страничната повърхност. Стойността на дължините на такива диагонали се определя въз основа на познанията за дължините на съответните ръбове и ъглите между тях. За да се определят диагоналите на паралелограмите, винаги се използват свойствата на триъгълниците.
2. Лежи в обема на призмата. Тези диагонали свързват не-един към един пикове на две бази. Тези диагонали са изцяло вътре в фигурата. Тяхната дължина е малко по-трудна за изчисляване, отколкото за предишния тип. Методът на изчисление включва отчитане на дължините на ръбовете и основата и паралелограмите. При правилните и правилните призми изчислението е сравнително просто, тъй като се извършва с помощта на питагоровата теорема и свойствата на тригонометричните функции.

По-долу са дадени примери за изчисляване на различни диагонали.

Диагонални страни на четириъгълна права призма

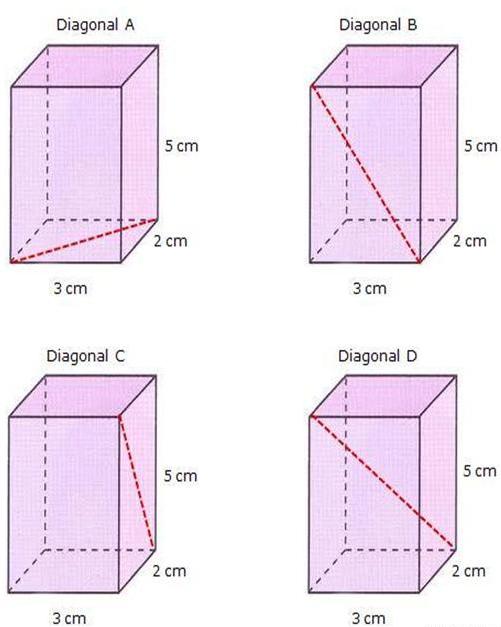
Фигурата по-горе показва четири идентични прави призми и са дадени параметрите на техните ръбове. На призмите на Диагонал А, Диагонал В и Диагонал С, пунктираната червена линия показва диагонала на три различни лица. Тъй като призмата е права с височина 5 см, а основата й е представена от правоъгълник със страни от 3 см и 2 см, лесно се намират маркираните диагонали. За да направите това, използвайте Питагоровата теорема.

Дължината на диагонала на основата на призмата (диагонал А) е равна на:

D _A = √ (3 ² +2 ² ) = 13 ≈ 3.606 cm.

За страничната повърхност на призмата, диагоналът е (виж Диагонал В):

D _B = √ (3 ² + 5 ² ) = 34 ≈ 5.831 cm.

Накрая, дължината на другата страна на диагонала е равна (виж Диагонал C)

D _C = √ (2 ² + 5 ² ) = 29 ≈ 5.385 cm.

Дължина на вътрешния диагонал

Сега изчисляваме дължината на диагонала на четириъгълната призма, която е показана на предишната фигура (Диагонал D). Не е толкова трудно да направите това, ако забележите, че това е хипотенуза на триъгълник, в която височината на призмата (5 cm) и диагоналът D _A, показани на фигурата в горния ляв ъгъл (Диагонал А), ще бъдат краката. Тогава получаваме:

D _D = √ (D _A ² + 5 ² ) = √ (2 ² +3 ² + 5 ² ) = 38 ≈ 6.164 cm.

Правилната призма е четириъгълна

Диагоналът на правилната призма, основата на която е квадрат, се изчислява по същия начин, както в примера по-горе. Съответната формула е:

D = √ (2 * a ² + c ² ).

Където а и с са дължините на основната страна и съответно на страничния ръб.

Забележете, че в изчисленията използвахме само Питагоровата теорема. За да се определят дължините на диагоналите на правилните призми с голям брой върхове (петоъгълни, шестоъгълни и т.н.), вече е необходимо да се използват тригонометрични функции.