Генетични алгоритми: същност, описание, примери, приложение
Идеята за генетичните алгоритми (GA) се появи доста отдавна (1950–1975), но те станаха истински обект на изследване едва през последните десетилетия. Г. Холанд се смяташе за пионер в тази област, който взел назаем много генетика и ги адаптирал за компютри. GAs широко се използват в системите за изкуствен интелект, невронни мрежи и оптимизационни проблеми.
Еволюционно търсене
Модели на генетични алгоритми са създадени въз основа на еволюцията в дивата природа и методите на случайно търсене. В същото време случайното търсене е реализация на най-простата еволюционна функция - случайни мутации и последваща селекция.
От математическа гледна точка еволюционното търсене не означава нищо повече от превръщането на съществуващо крайно множество от решения в ново. Функцията, отговорна за този процес, е генетичното търсене. Основната разлика на такъв алгоритъм от случайно търсене е активното използване на информацията, натрупана по време на повторения (повторения).
Защо се нуждаем от генетични алгоритми
GA има следните цели:
- обясни механизмите за адаптация както в естествената среда, така и в интелектуалната-изкуствена система;
- моделиране на еволюционни функции и тяхното приложение за ефективно търсене на решения на различни проблеми, предимно оптимизационни.
В момента, същността на генетичните алгоритми и техните модифицирани версии може да се нарече търсене на ефективни решения, като се отчита качеството на резултата. С други думи, намирането на най-добрия баланс между производителност и точност. Това се дължи на добре познатата парадигма на "оцеляване на най-силния индивид" в несигурни и размити условия.
Характеристики на GA
Ние изброяваме основните разлики на GA от повечето други методи за намиране на оптималното решение.
- работа с параметрите на задачата, кодирана по определен начин, а не директно с тях;
- търсенето на решение възниква не чрез уточняване на първоначалното приближение, а в набора от възможни решения;
- използване само на целевата функция, без да се прибягва до неговите производни и модификации;
- прилагане на вероятностен подход към анализа, вместо строго детерминистичен.
Критерии за ефективност
Генетичните алгоритми правят изчисления на базата на две условия:
- Изпълнете определен брой повторения.
- Качеството на откритото решение отговаря на изискванията.
Ако едно от тези условия е изпълнено, генетичният алгоритъм ще спре да извършва допълнителни повторения. В допълнение, използването на ГА в различни области на пространството за решения им позволява да намерят много по-добри нови решения, които имат по-подходящи стойности на целевата функция.
Основна терминология
Поради факта, че GA се основава на генетиката, по-голямата част от терминологията съответства на нея. Всеки генетичен алгоритъм работи въз основа на първоначалната информация. Наборът от начални стойности е популацията t t = {n 1 , n 2 , ..., n n }, където n i = {r 1 , ..., r v }. Ще разгледаме по-подробно:
- t е номерът на итерацията. t 1 , ..., t k - означава повторение на алгоритъма от номер 1 до k и при всяка итерация се създава нова популация от решения.
- n е размерът на популацията Pt.
- 1 , ..., п i - хромосома, особь, или организм. n 1 , ..., n i - хромозома, индивид или организъм. Хромозома или верига е кодирана последователност от гени, всеки от които има пореден номер. Трябва да се има предвид, че хромозомата може да бъде специален случай на индивид (организъм).
- rv са гени, които са част от кодираното решение.
- Локусът е последователният номер на ген в хромозома. Алел е генна стойност, която може да бъде както цифрова, така и функционална.
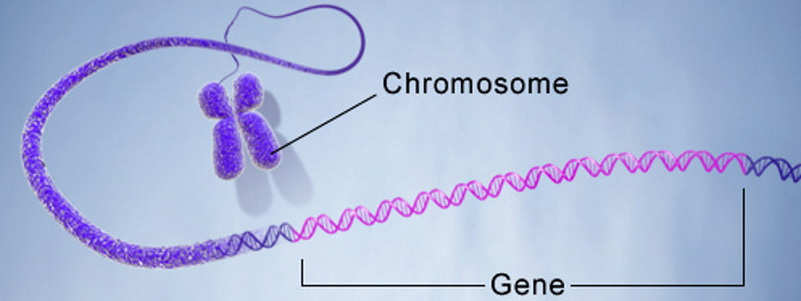
Какво означава "кодиран" в контекста на GA? Обикновено всяка стойност се кодира на базата на азбука. Най-простият пример е преобразуването на числа от десетичната система в двоичното представяне. По този начин азбуката е представена като множеството {0, 1}, а числото 157 10 ще бъде кодирано от хромозома 100111012, състояща се от осем гена.
Родители и потомци
Родителите са елементите, избрани в съответствие с дадено условие. Например, често това състояние е инцидент. Избрани елементи, дължащи се на операции на кръстосване и мутация, пораждат нови, които се наричат потомци. По този начин родителите по време на изпълнението на една итерация на генетичния алгоритъм създават ново поколение.
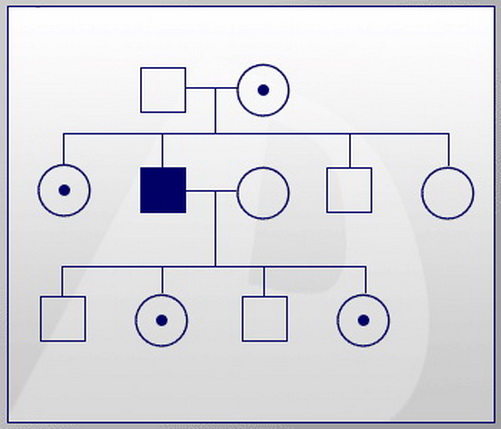
И накрая, еволюцията в този контекст ще бъде редуването на поколенията, всяко ново от които се отличава с набор от хромозоми за по-добра фитнес, т.е. по-подходящо съответствие с определените условия. Общият генетичен фон в процеса на еволюцията се нарича генотип, а формирането на връзката на организма с външната среда се нарича фенотип.
Фитнес функция
Магията на генетичния алгоритъм във фитнес функцията. Всеки индивид има своя собствена стойност, която може да се научи чрез функцията на адаптация. Неговата основна задача е да оцени тези стойности за различни алтернативни решения и да избере най-добрата. С други думи, най-силният.
При оптимизационните задачи функцията на фитнеса се нарича мишена, в теорията на контрола - грешка, в теорията на игрите - функция на стойността и т.н. Какво точно ще бъде представено като функция на адаптацията зависи от проблема, който трябва да бъде решен.
В крайна сметка може да се заключи, че генетичните алгоритми анализират популация от индивиди, организми или хромозоми, всяка от които е представена от комбинация от гени (набор от някои стойности) и търсят оптимално решение, превръщайки индивидите от популацията чрез изкуствена еволюция.
Отклоненията в една или друга посока от отделни елементи в общия случай са в съответствие с нормалния закон за разпределение на количествата. В същото време ГА осигурява наследственост на черти, най-приспособените от които са фиксирани, като по този начин осигурява най-доброто население.
Основен генетичен алгоритъм
Ние разлагаме на стъпки най-простия (класически) GA.
- Инициализиране на началните стойности, т.е. дефиницията на първичната популация, множеството от индивиди, с които ще се развива еволюцията.
- Установяване на първичната годност на всеки индивид в популацията.
- Проверете условията за прекратяване за повторения на алгоритъма.
- Използване на функцията за избор.
- Използването на генетични оператори.
- Създаване на ново население.
- Стъпки 2-6 се повтарят в един цикъл, докато се изпълни необходимото условие, след което се избира изборът на най-адаптирания индивид.
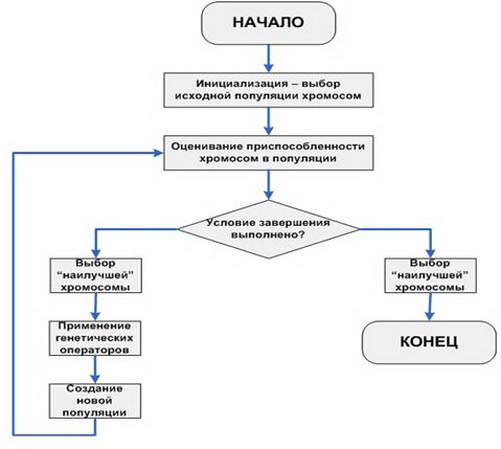
Нека да разгледаме накратко очевидните части на алгоритъма. Има две условия за прекратяване:
- Броят на повторенията.
- Качеството на решението.
Генетичните оператори са оператор на мутация и кросоувър оператор. Мутацията променя случайни гени с определена вероятност. По правило вероятността за мутация има ниска числена стойност. Нека поговорим повече за процедурата на генетичния алгоритъм "пресичане". Това се случва по следния принцип:
- За всяка двойка родители, съдържащи L гени, точката на пресичане Tsk i се избира случайно.
- Първият потомък е съставен от присъединяване [1; Tsk i ] гени на първия родител [Tsk i + 1 ; L] гени на втория родител.
- Вторият потомък е съставен по обратния начин. Сега към гените на втория родител [1; Tsk i ] добавя гените на първия родител в позициите [Tsk i + 1 ; L].
Тривиален пример
Ние решаваме проблема чрез генетичен алгоритъм, като използваме примера за търсене на индивид с максималния брой единици. Нека индивидът се състои от 10 гена. Определяме основната популация в размер на осем индивида. Очевидно е, че най-добрият човек трябва да бъде 1111111111. Нека да компенсираме решението на GA.
- Инициализация. Изберете 8 случайни индивида:
| n 1 | 1110010101 | n 5 | 0101000110 |
| n 2 | 1100111010 | n 6 | 0100110101 |
| n 3 | 1110011110 | n 7 | 0110111011 |
| n 4 | 1011000000 | n 8 | 0100001001 |
- Оценка на годността. Очевидно, в нашия генетичен алгоритъм, фитнес функцията F ще преброи броя на единиците във всеки индивид. Така имаме:
| n i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| F (n i ) | 6 | 7 | 8 | 3 | 4 | 5 | 7 | 3 |
Таблицата показва, че индивиди 3 и 7 имат най-голям брой единици и затова са най-подходящите членове на населението за решаване на проблема. Тъй като в момента няма решение с необходимото качество, алгоритъмът продължава да работи. Необходимо е да се извърши подбор на лица. За улеснение на обяснението, селекцията трябва да бъде случайна и ние получаваме извадка от индивиди {n 7 , n 3 , n 1 , n 7 , n 3 , n 7 , n 4 , n 2 } - това са родителите на новата популация.
- Използването на генетични оператори. Отново, за простота, ние приемаме, че вероятността от мутации е 0. С други думи, всичките 8 индивида предават гените си такива, каквито са. За да пресечем, правим двойки индивиди случайно: (n 2 , n 7 ), (n 1 , n 7 ), (n 3 , n 4 ) и (n 3 , n 7 ). По същия случаен начин се избират пресечните точки за всяка двойка:
| двойка | (стр 2 , стр 7 ) | (n 1 , n 7 ) | (p 3 , p 4 ) | (стр 3 , стр 7 ) |
| родители | [1100111010] [0110111011] | [1110010101] [0110111011] | [1110011110] [1011000000] | [1110011110] [0110111011] |
| Tsk i | 3 | 5 | 2 | 8 |
| потомци | [1100111011] [0110111010] | [1110011011] [0110110101] | [1111000000] [1010011110] | [1110011111] [0110111010] |
- Съставяне на ново население, състоящо се от потомци:
| n 1 | 1100111011 | n 5 | 1111000000 |
| n 2 | 0110111010 | n 6 | 1010011110 |
| n 3 | 1110011011 | n 7 | 1110011111 |
| n 4 | 0110110101 | n 8 | 0110111010 |
- Оценяваме годността на всеки индивид от новото население:
| n i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| F (n i ) | 7 | 6 | 7 | 6 | 4 | 6 | 8 | 6 |
По-нататъшни действия са очевидни. Най-интересното в GA е, ако преценим средния брой единици във всяка популация. При първото население средно за всеки индивид е имало 5.375 единици, в популацията на потомците - 6.25 единици на човек. И такава характеристика ще се наблюдава дори ако по време на мутациите и пресичането на индивида с най-голям брой единици в първата популация се загуби.
План за изпълнение
Създаването на генетичен алгоритъм е доста сложна задача. Първо, ще изброим плана под формата на стъпки, след което ще разгледаме всеки един от тях по-подробно.
- Определение на представяне (азбука).
- Дефиниция на оператори с произволна промяна.
- Определение за оцеляване на индивидите.
- Генериране на първичната популация.
Първият етап казва, че азбуката, в която ще бъдат кодирани всички елементи на набор от решения или население, трябва да бъде достатъчно гъвкава, за да позволи на необходимите произволни пермутации да бъдат изпълнени едновременно и да оцени годността на елементите, както първичните, така и тези, които са преминали през промените. Математически е установено, че е невъзможно да се създаде идеална азбука за тези цели, поради което компилирането й е една от най-трудните и решаващи стъпки за осигуряване на стабилна работа на ГА.

Също толкова трудно е да се определят изявленията за промяна и да се създават потомци. Има много оператори, които са в състояние да изпълнят необходимите действия. Например от биологията е известно, че всеки вид може да се размножава по два начина: сексуално (чрез кръстосване) и асексуален (чрез мутации). В първия случай родителите обменят генетичен материал, а във втория - се случват мутации, определени от вътрешните механизми на тялото и външното влияние. Освен това могат да се използват репродуктивни модели, които не съществуват в дивата природа. Например, използвайте гените на три или повече родители. По същия начин, преминаването на мутация в генетичен алгоритъм може да включва разнообразен механизъм.
Изборът на метод за оцеляване може да бъде изключително измамен. Има много начини в генетичния алгоритъм за размножаване. И както показва практиката, правилото за "оцеляването на най-силния" не винаги е най-доброто. При решаването на сложни технически проблеми често се оказва, че най-доброто решение идва от множество средни или дори по-лоши. Затова често се приема вероятностен подход, според който най-доброто решение има по-голям шанс за оцеляване.

Последният етап осигурява гъвкавостта на алгоритъма, който никой друг няма. Първоначалната популация от решения може да се определи или въз основа на всички известни данни, или по напълно случаен начин чрез просто пренареждане на гените вътре в индивидите и създаване на случайни индивиди. Въпреки това, винаги си струва да си припомним, че ефективността на алгоритъма зависи от първоначалната популация.
ефикасност
Ефективността на генетичния алгоритъм зависи изцяло от правилността на стъпките, описани в плана. Особено влиятелен елемент тук е създаването на основно население. Има много подходи за това. Ние описваме няколко:
- Създаване на пълно население, което ще включва всякакви опции за физически лица в дадена област.
- Произволно създаване на индивиди въз основа на всички валидни стойности.
- Създаване на случайно на отделни индивиди, когато между допустимите стойности е избран диапазонът за генериране.
- Комбинирането на първите три начина за създаване на население.

Така можем да заключим, че ефективността на генетичните алгоритми зависи до голяма степен от опита на програмиста в тази област. Това е едновременно недостатък на генетичните алгоритми и тяхното предимство.