Закон за запазване на енергията: описание и примери

Потенциалната енергия е по-скоро абстрактна стойност, защото всеки обект, който има определена височина над повърхността на Земята, вече има определено количество потенциална енергия. Изчислява се чрез умножаване на скоростта. свободно падане до височина над Земята, както и до масата. Ако тялото се движи, можете да говорите за наличието на кинетична енергия.

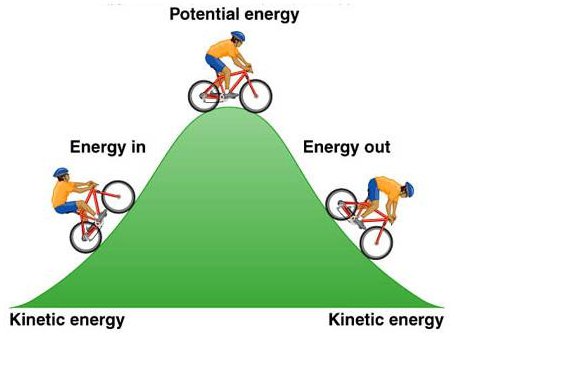
Формула и описание на закона

Резултатът от добавянето на кинетична и потенциална енергия в система, затворена от външно въздействие, части от която взаимодействат поради еластичните сили и сила, не се променя - това е законът за запазване на енергията в класическата механика. Формулата на този закон е следната: Ek1 + Ep1 = Ek2 + Ep2. Тук Ek1 е кинетичната енергия на определено физическо тяло в определен момент във времето, а Ep1 е потенциал. Същото важи и за Ek2 и Ep2, но вече в следващия период от време. Но този закон е валиден само ако системата, в която работи, е затворена (или консервативна). Това предполага, че стойността на пълния механична енергия не се променя, когато в системата действат само консервативни сили. Когато неконсервативните сили влизат в игра, част от енергията се променя, приемайки други форми. Такива системи се наричат ​​дисипативни. Законът за запазване на енергията действа, когато външните сили не засягат тялото.

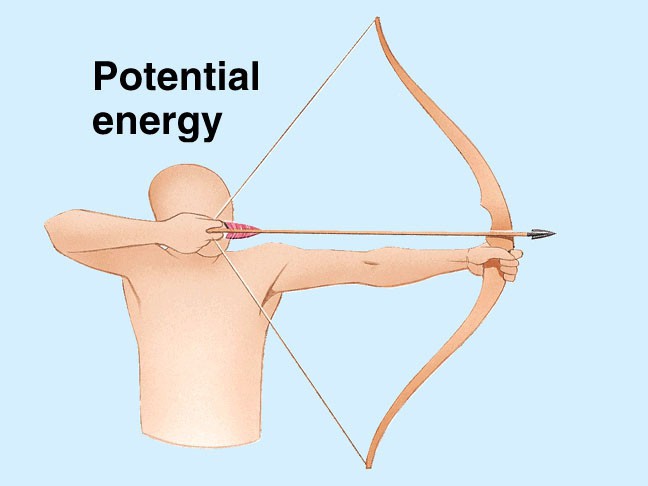
Пример за проявлението на закона

Един от типичните примери, илюстриращи описания закон, е експеримент с топка от стомана, която пада върху плоча от същото вещество или върху стъклена чаша, отскачаща се от него до почти същата височина, каквато беше преди падането. Този ефект се постига благодарение на факта, че когато се движи обектът, енергията се преобразува няколко пъти. Първоначално стойността на потенциалната енергия започва да се стреми към нула, докато кинетиката се увеличава, но след сблъсък става потенциалната енергия на еластичната деформация на топката.

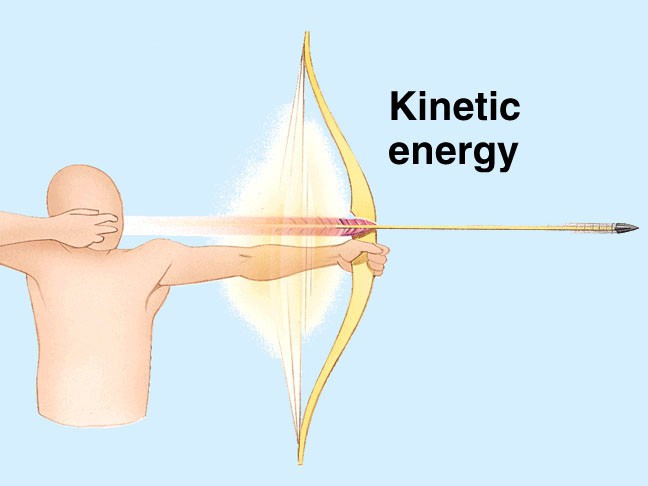
Това продължава до момента, в който обектът е напълно спрян, в който започва движението си нагоре поради силите на еластичната деформация на плочата и падналия обект. Но в същото време влиза в действие потенциална енергия гравитацията. Тъй като топката се разбира на приблизително същата височина, от която е паднала, кинетичната енергия в нея е същата. В допълнение, сумата от всички енергии, действащи върху движещ се обект, остава същата през целия описан процес, потвърждавайки закона за запазване на общата механична енергия.

Еластична деформация - какво е това?

За да разберем напълно приведения пример, си заслужава да разберем по-пълно каква е потенциалната енергия на еластичното тяло - това понятие означава да притежаваме еластичност, която, когато всички части на дадена система са деформирани, може да се върне в състояние на покой, извършвайки някаква работа върху тела, с които физически обект. Работата на силите на еластичност не се влияе от формата на траекторията на движение, тъй като работата, извършена за сметка на тях, зависи само от позицията на тялото в началото и края на движението.

Когато са външни сили

Но законът за запазване не се прилага за реални процеси, в които се включва сила на триене. Пример за това е падащ предмет на земята. По време на сблъсъка кинетична енергия и силата на съпротивлението се увеличава. Този процес не се вписва в рамката на механиката, тъй като телесната температура се повишава поради нарастващата съпротива. От гореизложеното следва, че законът за запазване на енергия в механиката има сериозни ограничения.

термодинамика

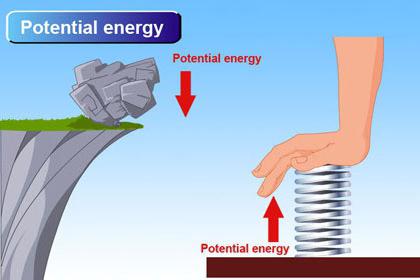
Първият закон на термодинамиката казва: разликата между количеството топлина, акумулирана от работата, извършена върху външни обекти, е равна на промяната вътрешна енергия тази неконсервативна термодинамична система.

Но това твърдение най-често се формулира в различна форма: количеството топлина, получена от термодинамичната система, се изразходва за работа върху обекти извън системата, както и за промяна на количеството енергия в системата. Според този закон, той не може да изчезне, превръщайки се от една форма в друга. От това следва, че създаването на машина, която не консумира енергия (т. Нар. Perpetuum mobile) е невъзможно, тъй като системата ще се нуждае от енергия отвън. Но мнозина все още упорито се опитват да я създадат, без да вземат предвид закона за запазване на енергията.

Пример за проявлението на закона на консервацията в термодинамиката

Експериментите показват, че термодинамичните процеси не могат да бъдат обърнати. Пример за това е контактът на тела с различни температури, при които по-нагрятото ще отделя топлина, а второто е да го получи. Обратният процес по принцип е невъзможен. Друг пример е прехвърлянето на газ от една част на съда към друга след отварянето на преградата между тях, при условие че втората част е празна. Веществото в този случай никога няма да започне да се движи спонтанно в обратна посока. От гореизложеното следва, че всяка термодинамична система се стреми към състояние на покой, в което отделните му части са в равновесие и имат една и съща температура и налягане.

хидродинамика

Прилагането на закона за запазване в хидродинамичните процеси се изразява по принцип, описано от Бернули. Това звучи така: сумата от налягането както на кинестетичната, така и на потенциалната енергия на единица обем е една и съща във всяка дадена точка в потока на течност или газ. Това означава, че за измерване на дебита е достатъчно да се измери налягането в две точки. Това се прави, като правило, с манометър. Но законът на Бернули е валиден само ако въпросната течност е с нулев вискозитет. За да се опише потока на реалните флуиди, се използва интегралът на Бернули, което предполага добавяне на термини, които отчитат съпротивлението.

електродинамика

При електрификацията на две тела броят на електроните в тях остава непроменен, поради което положителният заряд на едно тяло е равен по величина на отрицателния заряд на другия. Така законът за запазване на електрическия заряд предполага, че в електрически изолирана система сумата от зарядите на неговите тела не се променя. Това твърдение е вярно и когато заредените частици претърпяват трансформации. Така, когато се сблъскат 2 неутрално заредени частици, сумата от техните заряди все още остава нула, тъй като положително заредена частица се появява заедно с отрицателно заредена частица.

заключение

Законът за запазване на механичната енергия, инерцията и момента - фундаменталните физични закони, свързани с хомогенността на времето и неговата изотропия. Те не се ограничават само до рамката на механиката и са приложими както за процесите, протичащи в космическото пространство, така и за квантовите явления. Законите на консервацията позволяват да се получат данни за различни механични процеси, без да се изследват с помощта на уравненията на движението. Ако някой процес на теория игнорира тези принципи, провеждането на експерименти в този случай е безсмислено, тъй като те ще бъдат неефективни.