Диагонален куб: какво е това и как да го намерим?
Диагоналът на куба е един от елементите, които ще трябва да знаете, когато решавате проблеми в стереометрията по време на завършването на финалната работа по математика за курса на основното училище.
Някои кубически теории
Този полиедър се отнася директно до прави паралелепипеди и призми. Той е специален случай и на двете. В основата на куба лежи квадрат, а страничните му ръбове са равни на страната на дадения квадрат. Така че всичко три измерения имат едни и същи стойности.
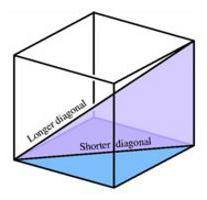
Всичките шест лица на куба са квадратчета. Дължината на всяка от 12-те ръбове е една и съща.
Във всяко от лицата можете да нарисувате диагонал, дължината на който е лесно да се намери с помощта на питагоровата формула. В допълнение, самият куб има диагонал. Има само четири от тях. Диагоналът на куба се изчертава така, че да започва от върха на долната основа. Краят на този сегмент е в горната част на горната основа, но така, че да не съвпада с диагонала на квадрата.
Важни формули
Те ще трябва да въведат едно и също наименование. Най-често буквата “а” е страната на куба. "V" е в обем. "S" и "d" са съответно площта и диагонала. Радиуси "R" и "r" на описаните и вписани сфери.
V = a³ (# 1) се използва за намиране на обема;
S = a² (# 2) формула за областта на лицето;
S = 6a² (№3) е необходимо да се изчисли площта на цялата повърхност на куба;
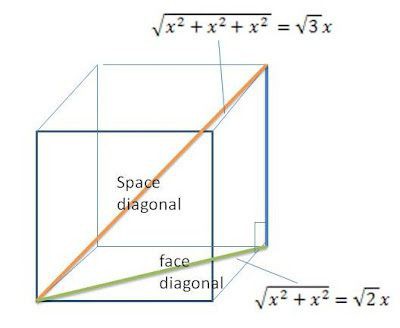
ако искате да знаете диагонала на куб, формулата ще бъде такава d = a √ 3 (# 4);
полезно за търсене на радиуси: R = (a / 2) * √3 и r = а / 2 (No. 5) и (No. 6) .
Няколко думи за симетрията на куба
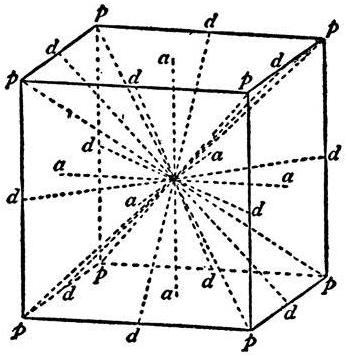
Това геометрично тяло има два вида симетрия: по отношение на точка и ос. За да намерите първата, трябва да начертаете диагонал на куба, след това на втория, за да намерите точката на тяхното пресичане. Тя ще бъде център на симетрия.
Всички линии, които минават през тази точка и са перпендикулярни на лицата, са осите на симетрията.
Примери за задачи от изпита
Те се използват в част Б, т.е. където трябва да се изпълни подробно решение на задачата. Просто изберете отговора тук няма да успее. Ето защо е необходимо да се познават формулите и да могат да се прилагат в различни ситуации.
Първата група задачи. Той познава дължината на диагонала на куба. Необходимо е да се изчисли обемът му или да се открие площта.
Например известна стойност може да бъде равна на единица. След това, за да разберете обема и площта, трябва да използвате формули № 1 и 3. Но те говорят за ръба, и с диагонал. Ще трябва да напишете друга формула.
Ако погледнете чертежа на куба и диагоналът в него, можете да видите какви форми правоъгълен триъгълник. Единият му крак съвпада с ръба, вторият с диагонала на лицето, а диагоналът на куба е хипотенузата.
Тогава можем да напишем Питагоровата теорема: квадратът на хипотенузата (d 2 ) е равен на квадрата на първия крак (a 2 ), сгънат с квадрата на втория (a2) 2 . След извършване на трансформациите се оказва, че ръбът на куба е свързан с диагонала, който е равен на d, разделен от корен квадратен от 3.
Сега можете да започнете да намирате ръба и след това да изчислите обема и областта. В специфичен проблем a = 1 / =3 = ()3) / 3. Тогава обемът е равен на ()3) / 9. Районът е два.
Втората група задачи. Обратно на предишното, когато областта или обемът са известни, и е необходимо да се изчисли стойността на диагонала на куба.
Пример за това е проблемът, при който повърхностната площ е известна и тя е равна на 8. Ще бъде необходимо да се използва формула № 3 и зависимостта, получена в предишния проблем.
Първо трябва да знаете дължината на ръба. Тя е равна на квадратен корен от частичния S на 6. След като замените известна величина, a = √ (8/6) = √ (4/3). Сега остава да се изчисли диагоналът на куба, да се подреди този номер и да се умножи с 3. Оказва се, че 2.
Третата група задачи съдържа данни за диагонала на лицето на куба. Те трябва да разпознаят обема или областта на тялото. Възможно е също така вариант, при който трябва да се изчисли диагоналът на куба. При тези проблеми мотивите следват същия път, който беше разгледан в предишните случаи.