Знаменател на геометрична прогресия: формули и свойства
Геометричната прогресия, заедно с аритметиката, е важна цифрова поредица, която се изучава в курса по алгебра в 9-ти клас. В тази статия разглеждаме знаменателя на геометричната прогресия и как нейната стойност влияе на нейните свойства.
Определение за прогресия на геометричното
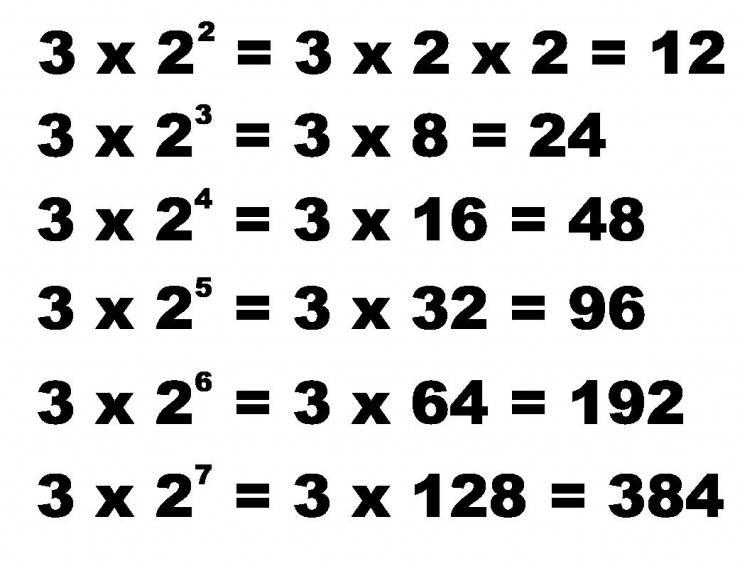
Да започнем с това, даваме дефиницията на този брой серии. Такава поредица от рационални числа, която се формира от последователно умножаване на първия й елемент с постоянно число, наречено знаменател, се нарича геометрична прогресия.
Например, числата в ред 3, 6, 12, 24, ... е геометрична прогресия, защото ако умножим 3 (първият елемент) с 2, получаваме 6. Ако 6 се умножи по 2, получаваме 12 и т.н.
Членовете на разглежданата последователност обикновено се обозначават със символа a i , където i е цяло число, показващо броя на елемента в серията.
Горната дефиниция за прогресия може да бъде написана на езика на математиката, както следва: a n = b n-1 * a 1 , където b е знаменателят. Лесно е да се провери тази формула: ако n = 1, тогава b 1-1 = 1, и получаваме 1 = a 1. Ако n = 2, тогава a n = b * a 1 , и отново стигаме до дефиницията на разглежданата поредица от числа. , Подобни аргументи могат да бъдат продължени при големи стойности на n.
Знаменателят на прогресията на геометричното
Числото b напълно определя естеството на цялата серия от числа. Знаменателят b може да бъде положителен, отрицателен и също да има стойност, по-голяма от една или по-малка. Всички тези опции водят до различни последователности:
- b> 1. Съществува нарастващ брой рационални числа. Например, 1, 2, 4, 8, ... Ако елемент a 1 е отрицателен, тогава цялата последователност ще се увеличи само в абсолютна стойност, но ще намалее по отношение на знака на числата.
- b <-1. В този случай става дума за променлива серия, т.е. съседните елементи ще се различават по знака. Например, 1, -2, 4, -8, 16, ...
- -1 <b <1. Това е специален случай, който има собствено име - намаляваща безкрайна геометрична прогресия. Неговата основна характеристика е, че независимо от знака на знаменателя, тя се стреми към някаква крайна сума, когато добавя безкраен брой от нейните елементи.
- b = 1. Често такъв случай не се нарича прогресия, тъй като има обичайната поредица от еднакви рационални числа. Например, -4, -4, -4.
Формула за сумата
Преди да пристъпим към разглеждане на конкретни задачи, като използваме знаменателя на въпросния тип прогресия, трябва да дадем важна формула за сумата от първите n елемента. Формулата има следния вид: S n = (b n - 1) * a 1 / (b - 1).
Можете да получите този израз сам, ако разглеждате рекурсивна последователност на членове на прогресия. Също така имайте предвид, че в горната формула е достатъчно да се знае само първият елемент и знаменателят, за да се намери сумата на произволен брой членове.
Безкрайно намаляваща последователност
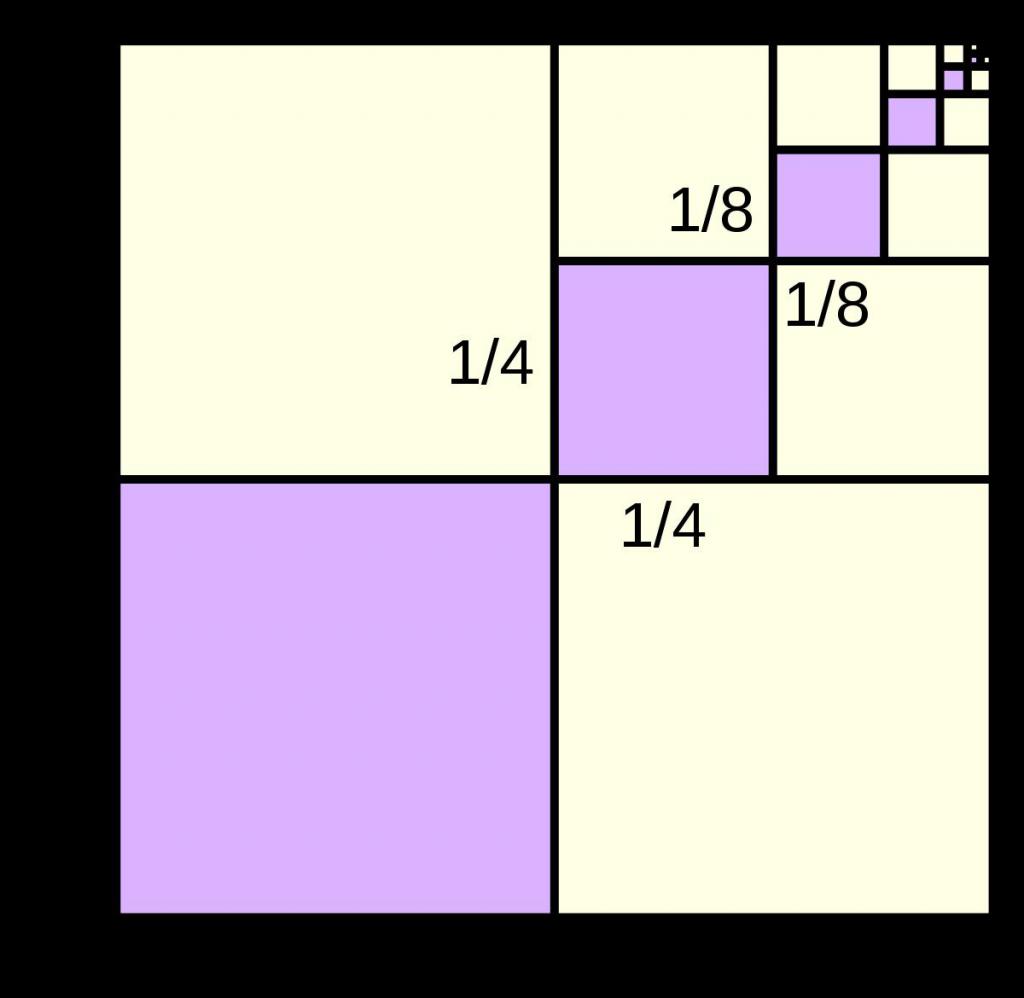
На него беше дадено обяснение какво е то. Сега, знаейки формулата за S n , приложете го към този брой серии. Тъй като всеки брой, чийто модул не надвишава 1, се стреми към нула, когато е издигнат до големи градуси, т.е. b ∞ => 0, ако -1 <b <1 (| b | <1), тогава общата формула за сумата се превръща в следният израз: S ∞ = a 1 / (1 - b).
Тъй като разликата (1 - b) винаги ще бъде положителна, независимо от стойността на знаменателя, знакът на сумата на намаляващата безкрайна прогресия на геометричното S ∞ е еднозначно определен от знака на първия му елемент a 1 .
Сега ще разгледаме няколко задачи, където ще покажем как да приложим знанията, придобити върху конкретни числа.
Проблем номер 1. Изчисляване на неизвестните елементи на прогресията и размера
Като се има предвид прогресията на геометричното, знаменателят на прогресията 2, и първият му елемент 3. Какво ще бъдат неговите 7-и и 10-и членове, и каква е сумата от нейните седем начални елемента?
Състоянието на проблема е достатъчно просто и включва директно използване на горните формули. Така че, за да изчислим елемента с числото n, използваме израза a n = b n-1 * a 1 . За 7-мия елемент имаме: a 7 = b 6 * a 1, замествайки известните данни, получаваме: a 7 = 2 6 * 3 = 192. Продължаваме по същия начин за 10-ти член: a 10 = 2 9 * 3 = 1536 ,
Използваме добре познатата формула за сумата и определяме тази стойност за първите 7 елемента от серията. Имаме: S 7 = (2 7 - 1) * 3 / (2 - 1) = 381.
Задача номер 2. Определяне на сумата на произволните елементи на прогресията
Нека -2 е равно на знаменателя на прогресията в геометричната прогресия b n-1 * 4, където п е цяло число. Необходимо е да се определи сумата от 5-ти до 10-ти елемент от тази серия включително.
Поставеният проблем не може да бъде решен директно чрез познати формули. Тя може да бъде решена с два различни метода. За пълнота ще дадем и двете.
Метод 1. Неговата идея е проста: необходимо е да се изчислят двете съответни суми на първите членове и след това да се извадят един от друг. Изчисляваме по-малката сума: S 10 = ((-2) 10 - 1) * 4 / (-2 - 1) = -1364. Сега изчисляваме голямо количество: S 4 = ((-2) 4 - 1) * 4 / (-2 - 1) = -20. Отбележете, че в последния израз са обобщени само 4 термина, тъй като 5-та вече е включена в сумата, която се изчислява от състоянието на проблема. Накрая вземете разликата: S510 = S10-S4 = -1364 - (-20) = -1344.
Метод 2. Преди да замените числата и броячите, можете да получите формула за сумата между членовете m и n на разглежданата серия. Ние действаме по същия начин, както в метод 1, като работим само първо със символичното представяне на сумата. Имаме: S n m = (b n - 1) * a 1 / (b - 1) - (b m - 1 - 1) * a 1 / (b - 1) = a 1 * (b n - b m - 1 ) / (b - 1). Можете да замените известните числа в полученото изражение и да изчислите крайния резултат: S 10 5 = 4 * ((-2) 10 - (-2) 4 ) / (-2 - 1) = -1344.
Проблем номер 3. Какво е знаменателят?

Нека a 1 = 2, да намерим знаменателя на прогресията на геометричното, при условие че неговата безкрайна сума е 3 и е известно, че това е намаляваща серия от числа.
При състоянието на проблема не е трудно да се отгатне коя формула трябва да се използва за решаването му. Разбира се, за сумата на прогресията е безкрайно намалява. Имаме: S ∞ = a 1 / (1 - b). От където изразяваме знаменателя: b = 1 - a 1 / S ∞ . Остава да се заменят известните стойности и да се получи необходимия брой: b = 1 - 2/3 = -1 / 3 или -0.333 (3). Възможно е този резултат да се провери качествено, ако си припомним, че за този тип последователност модулът b не трябва да надхвърля 1. Както може да се види, | -1 / 3 | <1.
Проблем номер 4. Възстановяване на поредица от числа
Да се дадат 2 елемента от числова серия, например 5-та е 30, а 10-та е 60. Необходимо е да се реконструира цялата серия от тези данни, като се знае, че тя удовлетворява свойствата на геометричната прогресия.
За да се реши проблемът, е необходимо да започнете да пишете съответния израз за всеки познат член. Имаме: a 5 = b 4 * a 1 и a 10 = b 9 * a 1 . Сега разделяме второто изражение на първо, получаваме: a 10 / a 5 = b 9 * a 1 / (b 4 * a 1 ) = b 5 . Следователно, определяме знаменателя, като вземаме корен от пета степен от съотношението на термините, познати от условието на проблема, b = 1.148698. Полученото число се заменя в един от изразите за известен елемент, получаваме: a 1 = a 5 / b 4 = 30 / (1,148698) 4 = 17.2304966.
Така открихме, че знаменателят на прогресията bn е равен, а геометричната прогресия b n-1 * 17,2304966 = a n , където b = 1,148698.
Къде се прилага геометричната прогресия?

Ако на практика не е имало приложение на този брой редове, то неговото изследване би било сведено до чисто теоретичен интерес. Но такова приложение съществува.

Следват три най-известни примера:
- Парадоксът на Зенон, в който сръчният Ахил не може да настигне бавната костенурка, се решава с помощта на концепцията за намаляваща безкрайна последователност от числа.
- Ако сложите житни зърна на всяка клетка на шахматна дъска, сложете 1 зърно на 1-ва клетка, 2 на 2-ра, 2 на 3-та, и така нататък, тогава ще трябва 18446744073709551615 зърна да запълнят всички клетки на дъската!
- В играта "Кула на Ханой", за да се пренаредят дисковете от един прът към друг, е необходимо да се изпълнят 2 n - 1 операции, т.е. техният брой нараства експоненциално с броя на използваните дискове n.