Десетично закръгляване: учене по математика

Така че сега ще видим с вас как се извършва десетичното закръгляване. Всъщност този процес не е толкова сложен, колкото изглежда на пръв поглед. Вярно е, че някои ученици срещат трудности с тази тема. Нека им помогнем да разберат днешния ни въпрос.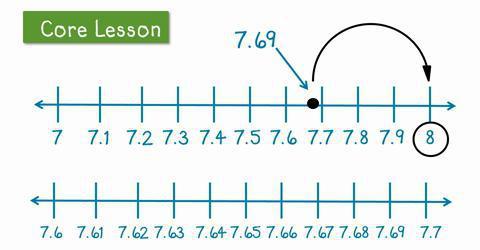

Понятие за десетичната дроб

Преди закръгляване знака след десетичната запетая, трябва ясно да разберем с какво трябва да се справим. Колкото по-добре разбираме този въпрос с вас, толкова по-лесно ще бъде в бъдеще.

Като цяло понятието "десетична дроб" се разкрива в 5-ти клас на училището. Това е вид число, състоящо се от цяло число и дробно, чийто знаменател е 10.

За да разберем ясно какво е изложено на риск, нека да разгледаме един пример и след това да проучим как се срещат десетичните числа. Този тип запис ще изглежда така: 5,26852. Ако преведете полученото число в част, можете да видите следното: 526852/100000. Десетичните дроби могат да бъдат както положителни, така и отрицателни. Това е всичко. Сега да тръгнем с вас към нашия проблем.

На части

Въпросът е, че закръгляването на десетичните дроби (клас 6) по правило се извършва на части. Първо, те заемат остатъка ("опашката"), т.е. тези числа, които са след запетая. Само тогава може да се вземе за цялата част.

Първото нещо, което се изисква от нас е да определим точността, с която ще заобиколим десетичните дроби. До десети, стотни, хилядни и така нататък. След това трябва да следвате някои правила, както и да научите един важен момент, който определено ще ви помогне да се справите със задачата. Нека работим с вас с ясен пример. Вземете произволен номер: 78,9563245. Именно върху него ще тестваме правилото за закръгляване на десетични знаци. Сега ще го опознаем.

Основно правило

Основният принцип, който трябва да научим, е как да се заменят числата при закръгляване. Работата е там, че е доста лесно да се направи. Нека видим как точно.

Ако имате 0, 1, 2, 3 или 4 като цифра, той автоматично се заменя с 0 и се отхвърля. След това се приближете до целочислената част и погледнете следващото число.

Веднага щом цифрата в цифрата е 5, 6, 7, 8 или 9, ще трябва да изхвърлите тази част и да добавите една към следващата (най-близо до целочислената част). Този процес трябва да се повтори до избраната точност на закръгляване. Нека сега погледнем един пример с вас. На него всичко ще изглежда по-ясно.

пример

Затова започваме да закръгляваме десетични знаци с вас. Работим с номера 78,9563245. Заобикаляме го до десетата, стотната и хилядната част. Да опитаме.

Първо, изхвърляме цялата част. Получаваме 0.9563245. Ще продължим да работим с вас с този конкретен номер. Започваме да закръгляваме с хилядни, постепенно увеличавайки точността.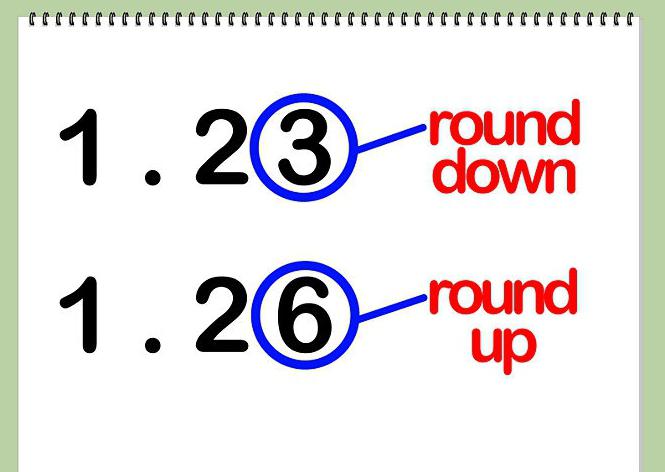

Номерът е 0.9563245. Придвижване към нула. Първото число от края е 5. Това означава, че ние го “конвертираме” в 0 и добавяме 4 към 4. Втората цифра - 4 + 1 = 5. Следователно, ние присвояваме единица на следващия знак и този се преобразува в 0.

Досега сме работили с вас: 0.95632 ⁽⁺¹⁾ . Закръгляването до хилядната е 3 цифри. Нека продължим да работим с вас. 2 + 1 = 3. Тази цифра е по-малка от 5s. Така че, просто го замени с 0 и премахване. Следващият етап е 3-ka. Нищо не се добавя към него. Просто замени с 0, тъй като е по-малко от 5. Направихме го с теб: 0.956. Сега можете да добавите цялата част: 78,956.

Но закръгляването на десетичните дроби не свършва дотук. Сега трябва да го държите на стотна. За да направим това, както и преди, поглеждаме последната цифра след запетая - 6. Според правилото, ние я заменяме с 0 и след това просто добавяме 1 към цифрата вляво от нея. Закръгляването до десетки тук не е много подходящо. Получаваме цяло число заедно с вас. В края на краищата, 6-ka ще бъде заменен с 0, единицата ще бъде добавена към 9, а накрая ще получим: 78.9 ⁽⁺¹⁾ . Ще стане 79. Това е всичко. Сега вече знаете как да кръглите фракции.