Ток в електрически вериги

Един от параметрите, характеризиращи поведението на електроните в електрическата верига, освен напрежение и ток, е мощност. Това е мярка за количеството работа, което може да се направи за единица време. Работата обикновено се сравнява с вдигане на теглото. Колкото по-голямо е теглото и височината му, толкова повече работи. Power определя скоростта на единица работа.

Мерни единици

Мощността на автомобила се изчислява в конски сили - единица за измерване, измислена от производителите парни машини с цел да се измери ефективността на техните единици в обичайния енергиен източник за времето. Силата на колата не казва колко висока може да стигне до хълма или колко тегло може да носи, а само показва колко бързо ще го направи.

Мощност на двигателя зависи от скоростта и въртящия момент на изходящия вал. Скоростта се измерва в обороти в минута. Въртящият момент е моментът на мощността на двигателя, който първоначално е бил измерен в lb-ft и сега е в нютонови метри или джаули.

100 л. Двигател на трактора а. се върти бавно, но с голям въртящ момент. Двигател с еднаква мощност се върти бързо, но с малък въртящ момент. Уравнението за изчисляване на мощността има следния вид:

P = 2π ST / 33000, където S е скоростта на въртене, rpm и T е въртящият момент.

Променливите тук са момент и скорост. С други думи, мощността е пряко пропорционална на ST: P ~ ST.

DC мощност

В електрически вериги, мощността е функционално зависима от напрежение и ток. Не е изненадващо, че той е подобен на горното уравнение Р = IU.

Но тук P не е пропорционално на тока, умножено по напрежението, но е равно на него. Изчислява се във ватове, съкратено като W.

Важно е да се знае, че токът и напрежението отделно не определят мощността, а само тяхната комбинация. Напрежението е работа на единица електрически заряд и текущата е скоростта на таксите. Напрежението (еквивалент на работа) е подобно на работата при вдигане на тежести в противовес на силата на тежестта. Токът (еквивалентен на скоростта) е подобен на скоростта на повдигане на тежестта. Тяхната работа е сила.

Подобно на тракторни и мотоциклетни двигатели, високоволтова верига с малък ток може да има същата мощност като верига с ниско напрежение и висок ток. Напрежението и токът извън връзката не могат да характеризират силата на веригата.

Една отворена верига с напрежение и нулева мощност не работи, независимо от височината на напрежението. В крайна сметка, според формулата, всичко, умножено по 0, дава 0: P = 0 U = 0. В затворена верига на свръхпроводящ проводник с нулево съпротивление, можете да постигнете ток при напрежение, равно на нула, което също не води до разсейване на енергия: P = I 0 = 0.

Конски сили и ватове означават едно и също: количеството работа, което може да се направи за единица време. Тези единици са взаимно свързани със съотношението

1 л. а. = 745.7 W

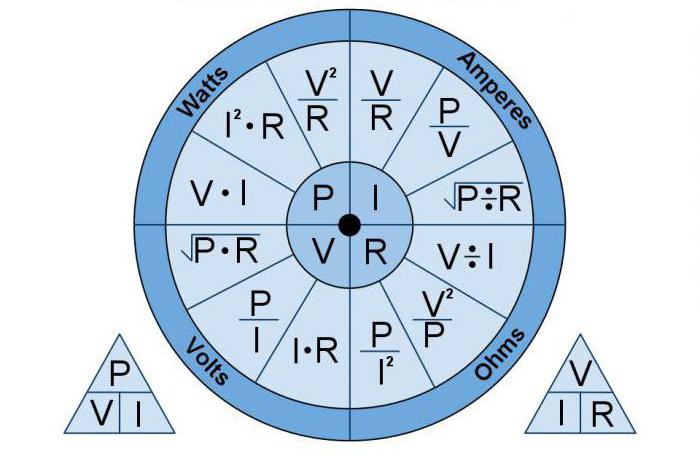
Пример за изчисление

Така, мощността на тока на електрическата верига във ватове е равна на произведението на напрежение и ток.

За да се определи, например, мощността на натоварване с съпротивление 3 ома, в схема с 12 V батерия, е необходимо, чрез прилагане на закона на Ом, да се намери ток

I = U / R = 12/3 = 4 A

Умножете силата на тока по напрежение и дайте желания резултат:

P = IU = 4 A 12 V = 48 W

Така лампата консумира 48 вата.

Какво се случва, когато напрежението се увеличи?

С напрежение 24 V и съпротивление 3 ома ток

I = U / R = 24/3 = 8 A

С удвояване на напрежението, силата на тока се удвои.

P = IU = 8 A 24 V = 192 W

Мощност също се увеличи, но повече. Защо? Тъй като това е функция на продукта на напрежението на ток, напрежение и ток се увеличава с 2 пъти, следователно, мощността се увеличава с 4 пъти. Това може да се провери чрез разделяне на 192 вата на 48, чийто коефициент е 4.

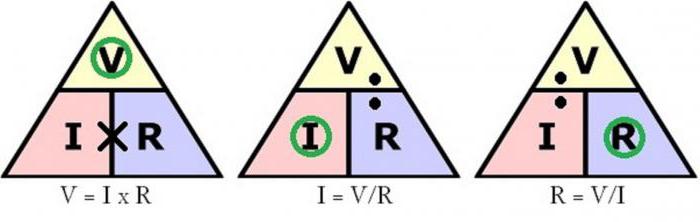
Варианти на формулата

Използвайки алгебра за преобразуване на формула, можете да вземете оригиналното уравнение и да я трансформирате за случаи, когато един от параметрите е неизвестен.

Ако са дадени напрежение и съпротивление:

P = (U / R) U или Р = U2 / R

С известна сила на тока и устойчивост:

Р = I (IR) или Р = I2R

Исторически факт: връзката между разсеяната сила и съпротивата е открита от Джеймс Прескот Жул, а не Георг Саймън Ом. Той е публикуван през 1841 г. като уравнение P = I ² R и се нарича Joule-Lenz law.

Уравнения на мощността:

• P = UI
• Р = I2R
• Р = U2 / R

Променлив ток

Законът Ом и Джаул - Ленц е създаден за постоянен ток но те са валидни и за моментни стойности на променлив ток и напрежение.

Моментната стойност на Р е равна на произведението на моментните стойности на тока и напрежението, като се отчита фазовото им изместване с ъгъл φ:

P (t) = U (t) I (t) = U _m cos ω I _m cos (ωt-φ) = (1/2) U _m I _m φ φ + (1/2) U _m I _m cos (2ωt- φ).

От уравнението следва, че моментната мощност има постоянен компонент и прави колебателни движения около средната стойност с честота, която е два пъти по-голяма от честотата на тока.

Средната стойност на P (t), която представлява практически интерес, е:

P = (Um I _m / 2) cosφ

Като се има предвид, че cos φ = R / Z, където Z = (R ² + (ω L - 1 / ω C) ² ) ^1/2 и U _m / Z = I _m ,

Р = (RI _m ² ) / 2

Тук I = I _m 2 ^-1/2 = 0.707 I _m - ефективната стойност на силата на тока, A.

По същия начин, U = U _m 2 ^-1/2 = 0.707 U _m - ефективно напрежение, V.

Средната мощност чрез ефективно напрежение и ток се определя от

P = UI cos φ, където cos φ е факторът на мощността.

P в електрическата верига преминава в топлина или друга форма на енергия. Най-високата активна мощност може да се постигне с cosφ = 1, т.е. при отсъствие на фазово изместване. Нарича се пълна сила.

S = UI = ZI2 = U2 / Z

Неговото измерение съвпада с размера на Р, но за целите на разликата S се измерва с волт-ампери, VA.

Степента на енергиен обмен в електрическа верига се характеризира с реактивна мощност.

Q = UI sinφ = UI _p = U _p I = XI ² = U ² / X

Той има измерението на активно и пълно, но за да го разграничи, се изразява чрез реактивни волта-ампери, VAR.

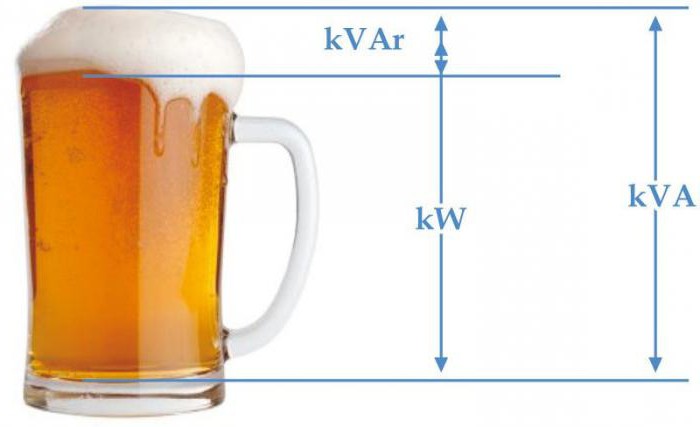
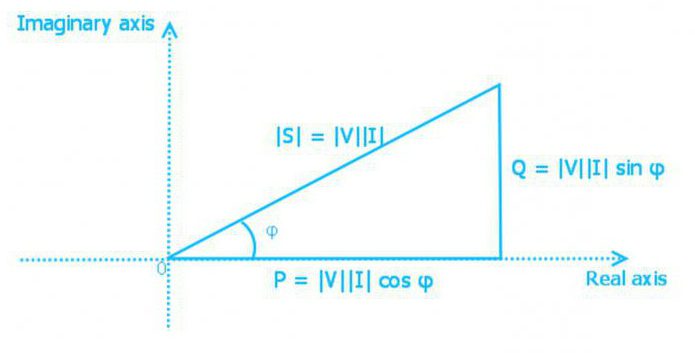
Мощност триъгълник

Мощността е активна, реактивна и пълна с взаимовръзка

S = (Р2 + Q2) ^1/2

Силата представлява като страна правоъгълен триъгълник. Използвайки законите на тригонометрията, може да се намери дължината на едната страна (количеството енергия от всякакъв тип) по две познати страни или по дължината на единия и на ъгъла. В такъв триъгълник активната мощност е съседният крак, реактивната мощност е обратна, а общата мощност е хипотенуза. Ъгълът между крака на активната мощност и хипотенузата е равен на фазовия ъгъл на импеданса Z на електрическата верига.

Сложната форма на тази връзка е следната:

S = P + jQ = UI cosφ + j UI sinφ = UI e ^jφ = UI *, където

S е комплексна мощност;

I * е комплексната конюгирана текуща стойност.

Истинският компонент на комплекса е активният, а въображаемият е реактивният.

Моментната обща мощност винаги остава постоянна.

Трифазно захранване

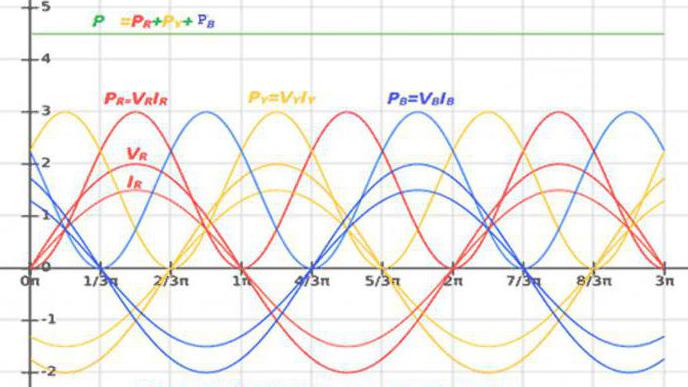
Натоварването на всяка фаза на трифазната верига преобразува енергията или я обменя с източник на енергия. В резултат P и Q схемите са равни на общата мощност на всички фази:

Р = Рг + P _y + Р _b ; Q = Q _r + Q _y + Q _b - звезда връзка;

P = _Пр + P _yb + P _br ; Q = Q _ry + Q _yb + Q _br - връзка "триъгълник".

Активната и реактивната мощ на всяка фаза се определят като в еднофазна верига.

Пълната мощност на трифазната верига:

S = (Р2 + Q2) ^1/2 ,

това, което в сложна форма изглежда

S = P + jQ = (P _r + P _y + P _b ) + j (Q _r + Q _y + Q _b ) = S _r + S _y + S _b = U _r I _r + U _y I _y + U _b I _б

Симетричното натоварване на фазите води до равенство на техните правомощия. Ето защо мощността на тока е три пъти по-голяма от активната и реактивната мощност на фазата:

P = 3P _f = 3 I _f U _f cosφ _f = 3 R _f I _f ²

Q = 3 Q _f = 3 I _f U _f sin = _f = 3 X _f I _f ²

S = 3 S _f = 3 I _f U _f

I _f и U _f тук могат да бъдат заменени с техните линейни стойности, като се има предвид, че за звездата U _f = U _l ; I _f = I _l , а за триъгълник U _f = U _l ; I _f = I _l 3 ^-1/2 :

P = 3 ^1/2 I _l U _l cosφ _f ;

Q = 3 ^{1/2 I _l U _l} sinφ _f ;

S = 3 ^{1/2 I _l U _l} .

Несинусоидален ток

Определението на Р в несинусоидална токова верига е подобно на дефиницията му в синусоидална токова верига, тъй като за период Т средната мощност

P = 1 / T

Активната мощност на тока се определя от сумата от P хармонични компоненти, включително константата, която е хармоника с нулева честота.

Реактивната мощност на ток по този начин е резултат от добавянето на Q на всяка хармоника.

Q = kUk I _k sinφ _k = Q _k

Общата мощност се определя от произведението на ефективния ток и напрежение:

S = I U.