Корелационен и регресионен анализ: приложение, основни етапи

Концепцията за корелационно-регресионен анализ предполага серия от операции, а именно определяне на близостта на връзката, нейната посока и установяване на уравнение, описващо формата на връзката. Този вид анализ съдържа два отделни компонента: корелационен и регресионен анализ.

Стойността и основните етапи на процеса на корелационния и регресионен анализ на икономическите явления

Корелационният и регресионен анализ е един от начините за решаване на проблеми и търсене на информация. Тя ви позволява да определите съвместното влияние на много взаимосвързани и едновременно действащи знаци, както и отделното влияние на всеки атрибут върху икономически феномен (процес). Благодарение на този вид анализ е възможно да се оцени степента на взаимовръзка между няколко характеристики, между характеристиките и получения резултат, както и да се моделира уравнение на регресия, описващо формата на взаимовръзка.

Етапи на анализ

Корелационният и регресионен анализ на икономическите процеси се разделя на няколко етапа:

1. Дефиниране на аргументи и предварителна обработка на условна информация.
2. Дефиниране на близост и форми на взаимовръзка между няколко знака.
3. Моделиране на представения икономически процес и анализ на получения модел.
4. Прилагане на крайните резултати за подобряване на планирането и управлението на модела.

Хомогенността на статистическата информация може да се определи, като се използват две техники. Първо, необходимо е да се определи и отхвърли стойността на факторите, които се различават рязко от всички количества. След това се извършва статистическо изследване на хомогенността чрез проверка на независимостта на извадката и нейната принадлежност към един комплект с нормално разпределение.

Регресионният модел се определя чрез метода на най-малките квадрати, който осигурява най-доброто приближение на оценката на резултата, определена чрез регресионното уравнение, на нейните фактори.

Корелационен и регресионен анализ: параметрите на създадения модел

Най-важните фактори, определящи характеристиките на модела, се считат за:

• Коефициентите на двойката корелация (демонстрират силата на връзката на два фактора).
• Коефициентът на множествена корелация (определя връзката на резултата и факторите).
• Коефициентите на частното определяне (показват ефекта на вариацията на аргумента върху изменението на желаната черта).
• Коефициентът на множественото определяне (показва делът на всички аргументи за промяната на желаната характеристика).
• частен коефициенти на еластичност (характеризират влиянието на факторите върху резултата, изразени в единична скала в проценти).

Цел на анализа

Основните задачи на корелационно-регресионния анализ са идентифицирането на фактори, които оказват значително влияние върху икономическия резултат на дадено явление или процес и използването на получената информация за подобряване на планирането на икономически процес или явление.

Методи за параметричен анализ

Всички производствени процеси са тясно свързани. Тази връзка е стохастична (резултатът зависи от много фактори) и функционална (резултатът се променя със същата сума като фактора). Стохастичната зависимост често има корелативен характер, т.е. стойността на един фактор едновременно съответства на няколко стойности на резултата, които имат напълно различни посоки.

Корелационна мрежа

Корелационната връзка може да има един или няколко фактор-признака, да има положителна или отрицателна насоченост, да бъде права или криволинейна (в зависимост от израза). Възможно е да се определи кой тип връзка е свързан чрез използване на корелационната решетка. Тя е изградена в правоъгълните оси на координатите.

Честотите, поставени близо до диагоналите, показват висока корелация на знаците. Честотите, разположени близо до диагонала, минаващи през долния ляв и десен горен ъгъл, показват положителната посока, а тези, преминаващи през горния ляв и десен долния ъгъл, показват обратната посока. Честотите, разположени във формата на дъга, показват криволинейна връзка и случайно разпръснати - за липсата на връзка.

Основният метод за корелационен анализ е линеен. коефициент на корелация. Може да приема стойности от -1 до +1. Колкото по-близо е стойността до 1, толкова по-силна е връзката между фактора и резултата. Положителните стойности показват пряка връзка, а отрицателните стойности показват обратна връзка. Коефициентът приема стойността "нула", ако няма връзка между знаците.

Непараметрични методи за анализ

Редица методи позволяват да се оцени връзката на явленията без количествено изразяване на признак и съответно параметри на разпределение. Те се наричат ​​непараметрични. Сред тях са:

• Kendall коефициент на корелация (определя връзката между количествените и качествените стойности на показателите, ако те са подложени на класиране).
• Коефициент на рангова корелация на Spearman (присвоява редици на всеки аргумент и резултат, на базата на който се определят разликите и се изчислява индикаторът).
• Коефициентът на корелация на знаците на Фехнер (определя броя на съвпаденията и несъответствията между отклоненията на аргументите и резултатите от тяхната средна стойност).
• Друг важен метод за корелационен и регресионен анализ е методът на най-малките квадрати, който позволява да се определи аналитичният израз на връзката на произтичащия признак и неговия фактор. Тя се състои в изграждане на система от уравнения и определяне на параметрите на тези уравнения.

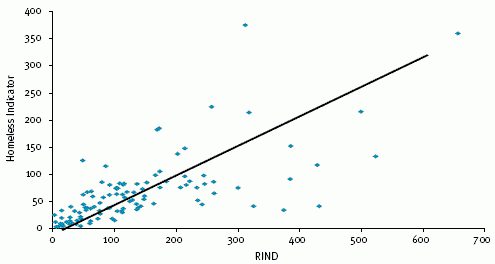
Корелационен и регресионен анализ: пример

Голямо разнообразие от видове и обекти на анализ се използват в статистиката и икономиката. Статистическите методи за анализ са насочени към изучаване на повтарящи се процеси, за да се направят дългосрочни прогнози за поведението на икономическите явления.

Например, за да се анализира социално-икономическото развитие на дадена територия, е необходимо да се проучат показателите за жизнения стандарт на населението. Корелационният и регресионен анализ в статистиката ви позволява да създавате уравнение на регресия и определят коефициентите на корелация, които демонстрират връзката между стандарта на живот и развитието на територията. Стандартът на живот се определя от дохода, а основният източник на доход е заплатата. В този случай факторът е нивото на заплатите, а резултатът е населението с ниски доходи.

Софтуер за анализ

За да улесните изчисленията, можете да извършите корелационен анализ в Excel. В тази програма има редица инструменти за улесняване на изчисленията. Сред тях е функцията "Корелация", която позволява да се формира матрица от коефициенти и различни параметри. Тя е изобразена под формата на маса. Корелационните коефициенти се използват като колони и редове. Въз основа на данните, получени в таблицата, ще бъде необходимо да се проведе корелационен анализ. Пример за последователността на анализа:

1. В командата “Service” изберете “Data analysis”.
2. Като инструмент за анализ изберете елемента "Корелация".
3. В прозореца, който се появява, в реда „Входен интервал”, задайте обхвата на анализираните данни, изберете позицията „Групиране” в реда „Изходни параметри”, въведете изходния диапазон на резултатите и натиснете „ОК”.

Резултатът е корелационна матрица, разположена в изходния диапазон. Вътре ще бъде посочен коефициентът на линейна корелация, който ще оцени степента и формата на връзката между индикаторите.

Анализ в Excel

В MS Excel, функцията "корелация" се използва за извършване на корелационен и регресионен анализ. Пример за изчисляване на коефициентите ще бъде разгледан по-късно. Тази функция образува матрица с коефициентите на близост в зависимост от различните параметри. В резултат на това се формира квадратна таблица, съдържаща коефициентите на корелация в пресечната точка на редове и колони.

За анализа е необходимо да се извършат редица конкретни действия:

1. Отворете командата "Сервиз", а в нея - "Анализ на данните".
2. В прозореца, който се появява, задайте елемента „Корелация“ в списъка „Инструменти за анализ“.
3. В прозореца “Корелация”, който се отваря, задайте интервала на въвеждане като диапазон от клетки, съдържащи анализираната информация (трябва да бъде поне две колони), отметка на опцията “Групиране”, а в полето Изходни параметри изберете горната лява клетка, където корелационна матрица.
4. Кликнете върху бутона OK.

В резултат на изчисленията ще се появи квадратна таблица с коефициенти на корелация.

Регресионен анализ в MS Excel

За да се изчисли линейно уравнение Регресиите, описващи връзката между факторите и резултата, се използват в MS Excel, статистическата функция „Linean“. За да я използвате, трябва:

1. Изберете празно място, в което ще се показват резултатите от анализа.
2. Отворете "Магистър на функциите", в него намерете категорията "Статистически", а в нея и функцията "Линеен" и щракнете върху OK.
3. В полето "Известни стойности на y " въведете обхвата на анализираните резултати в полето "Познати x стойности" - обхвата на анализираните фактори.
4. Полето "Константа" показва наличието на свободен термин в уравнението (1 - да, 0 - не), а в полето "Статистика" - необходимостта от показване на допълнителна информация (1 - ще се появи допълнителна информация, ще се появи 0 - само оценки на параметрите). По подразбиране можете да укажете и в двете полета 1.
5. Кликнете върху OK.

В горната част на предварително избраната област ще се появи началният елемент на таблицата. За да разкриете всички данни, трябва да натиснете F2, а след това едновременно клавишната комбинация Ctrl + Shift + Enter.

В резултат на това регресионната информация ще бъде показана като таблица от две колони и пет реда:

Резултатите трябва да бъдат заменени с уравнението на линейната регресия, което изглежда така: y = a + bx. Стойността от клетката в пресечната точка на ред 1 и колона 2 се заменя с коефициента a. Стойността в пресечната точка на ред 1 и колона 1 се използва като коефициент b.

Коефициентът на определяне показва каква част от резултата се обяснява с помощта на изследвания фактор. Останалата част от резултатите се определя от фактори, които не се отчитат в линейния модел.