Комбинаторика - какво е това? Елементи на комбинаториката
Специалистите в различни области трябва да решават комбинаторни проблеми: пренареждане на числа, знаци и други обекти. Например, ръководителят на магазина трябва да разпределя различни видове работа между работните машини. Комбинаториката е значим клон на математиката, който, както не е трудно да се отгатне, намира своята ниша в различни области и специалности: физика, биология, лингвистика, химия, инженерство, теория на кодирането и много други. Принципите на комбинаториката също са в основата на решаването на набор от вероятностни проблеми.
История на
Първите предпоставки на комбинаториката като наука се появяват през 16 век. Допринесли за развитието на тази област на знанието в голяма степен, очарование на хората от хазарта: карти, зарове, лотария загуби не само злато и бижута, но дворци и имоти. Ето защо, чудейки се например за това колко често можете да хвърлите добър набор от точки на костите или да получите два аса, хората постепенно стигнаха до основите на комбинаториката и вероятността. Дали комбинаториката помага на някой да спечели повече или да загуби по-малко? Въпросът е интересен, но неговото разглеждане е извън обхвата на тази статия.

Първият математик, който се интересуваше активно от комбинаториката, е италианският италианец Тарталия (1499-1557 г.), след него изтъкнати учени като Паскал, Ферма, Бернули, Лайбниц, Ойлер и др. все още остава, ако не и забавна игра с числа, а след това теория, която се използва изключително в хазарта и няма право да бъде използвана другаде.
Развитието на комбинаториката
Значителен напредък в комбинаториката се случи с настъпването на 20-ти век. компютри, програмиране и най-важното - дискретна математика. През този период комбинаториката достига върха на бързото си развитие и се превръща в пълноценна наука. Комбинаторните методи започват да се използват навсякъде:
- решаване на транспортни проблеми;
- график;
- изготвяне на планове за производство и продажба на стоки;
- в теорията на случайните процеси;
- по математическа статистика и теория на вероятностите;
- при подготовката и провеждането на експерименти;
- в шах;
- в термодинамиката;
- в геометрията;
- и в много други области.
Суеверни предизвикателства на лидерите
Имаше лидер в света, който вярваше, че числото 8 му носи тотални провали. Затова той реши да се отърве от всички цифри, които ще съдържат цифрата осем. Под негово ръководство работят 600 души. Всеки имаше идентификационен номер пропуск за работа, състоящ се от три числа. Без да се замисля два пъти, мениджърът реши да изключи числото 8 от броя на пропуските и тогава се зачуди дали има достатъчно различни номера за 600 души от диапазона от 000 до 999, което не включва 8?
Очевидното решение на този проблем е ръчно да се изпишат всички числа от 000 до 999 и да се пресекат онези, в които има осем. Възможно ли е проблемът да бъде решен по-прост? Ако за 999 числа задачата с изброяване на всички варианти изглежда осъществима, тогава диапазонът от 000000 до 999999 ще изисква много по-големи усилия. Тя е да спести време и усилия, предназначени за комбинаторни формули.
Решението на проблема за суеверния лидер
Друго решение е както следва. Премахвайки 8 от серията, получаваме, че 0, 1, 2, 3, 4, 5, 6, 7, 9 - тези девет числа са валидни. След това трябва да намерите всички двуцифрени числа, които не биха съдържали 8. Това се прави просто: трябва да вземете произволен номер от валидния и да го добавите към произволен номер от валидния. По този начин лесно ще получим всички двуцифрени числа, които отговарят на условията. В резултат на това получаваме, че всяка една цифра ще даде 9 различни двуцифрени числа. Общият брой на тези цифри ще бъде 9 * 9 = 9 2 = 81.
Продължавайки аналогията, можем да заключим, че за да се получат всички трицифрени числа без осмици, е необходимо да се припише трета цифра на съществуващите двуцифрени числа, също и от допустимите стойности. Тогава ще разберем, че броят на тези цифри ще бъде 9 2 * 9 = 9 * 9 * 9 = 729. Така открихме, че ръководителят на нашия мениджър ще може лесно да осигури 600 служители с пропуски, които няма да съдържат 8. Опитайте се да решите проблема сами с петцифрени числа.
И какво ще стане, ако мениджърът не харесва номер 2? Оказва се, че броят на допустимите числа ще бъде 8, а именно: 0, 1, 3, 4, 5, 6, 7, 9. Тогава, след като оцени броя на комбинациите от числа без 2 и 8, можем да заключим, че техният брой е 8 * 8 * 8 = 512, и това очевидно не е достатъчно, за да осигури 600 души с пропуски. Комбинаториката е наука, която помага по-ефективно да отговори на тези въпроси, отколкото може да се направи чрез груба сила.
Проблем с лото
Всеки знае играта. Има чанта, в която са поставени бъчви с числа от 1 до 90. Билетите се разпределят между всички участници, в които е необходимо да се рисува върху определен брой клетки с номера. След това водещото лото излиза от чантата един от номерираните бъчви. Победителят ще бъде този, който е зачеркнал повечето от номерата в билета, което съвпада с тези, които домакинът на играта извади.

Веднъж Нина играе лото, помисли си. Тя често наблюдаваше как водещият получава същия номер от чантата. Но в същото време първите две кегове се оказаха еднакви по-рядко. После се зачуди колко пъти можеш да извадиш две барела от чантата? Елементи на комбинаториката помагат да се отговори на нейния въпрос.
Лото решение
Очевидно е, че първият барел може да има числа от 1 до 90. С други думи, има 90 начина да се извлече първата барел. Но какво да кажем за следващия? Ако например един буре № 63 е изваден от чанта, тогава в текущата игра няма да се случи отново.
Методът на таблицата ще ни помогне да решим проблема. Където в заглавието и в заглавната колона ще бъдат изписани номера от 1 до 90. По този начин, в пресечната точка на всяка линия и всяка колона ще има двойка числа, или чифт варели, извадени от торбата. В същото време на диагонала на масата ще бъдат разположени същите двойки числа. Това е невъзможно в зависимост от състоянието, тъй като след премахването на една цифра от торбата повторението му е невъзможно. Получете таблица със следната форма:
| 1 | 2 | ... | 90 | |
| 1 | х | 1, 2 | ... | 1, 90 |
| 2 | 2, 1 | х | ... | 2, 90 |
| ... | ... | ... | х | ... |
| 90 | 90, 1 | 90, 2 | ... | х |
Общо получаваме таблицата, в която броят на клетките е 90 * 90 = 8100. Трябва да се помни, че има 90 двойки цифри, разположени по диагонала, които са невъзможни според условията. Тогава отговорът на въпроса колко пъти можете да получите 2 барела от торбата ще бъде 8100 - 90 = 8010 опции.
Разсъждавайки малко по-различен начин, можете да стигнете до същия отговор. За първия варел има 90 опции. След извличането на първия, ще останат 89 опции за втория варел. Така общият брой на опциите ще бъде 90 * 89 = 8010. Елементите на комбинаториката могат да бъдат използвани по различни начини. Единственият въпрос е простотата и универсалността на метода. Например, методът на таблицата може да се използва за три бъчви, които трябва да бъдат извлечени в един ред, и очевидно това ще бъде границата. А за четири или повече?
Проблем с екипажа
Ако избора зависи от това кои обекти са били избрани по-рано, тогава е удобно да се покаже такъв процес като "дърво". В първата стъпка, тъй като много линии са изложени от една точка, тъй като са възможни избори в първата стъпка. В краищата на всеки ред има и толкова допълнителни линии, колкото може да бъде направено във втората стъпка и т.н. В резултат на това ще бъде съставен вид дърво или графика. Комбинаториката и теорията може да звучат доста объркващо и неразбираемо, затова нека погледнем един пример.
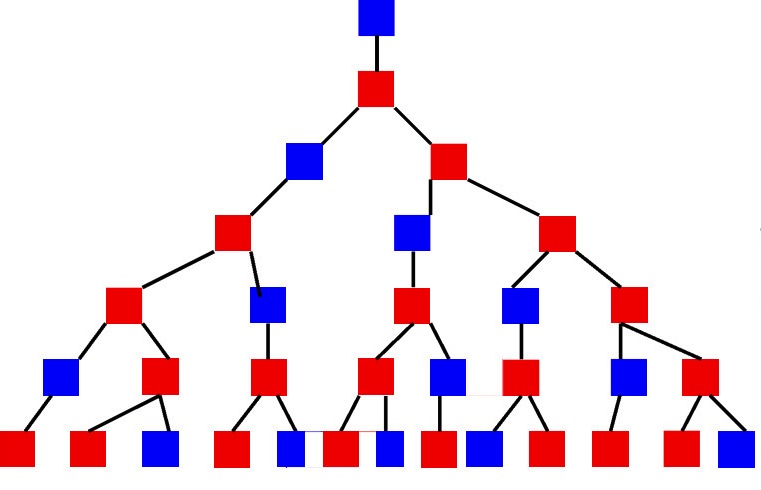
Преди началото на експедиционната година, ръководството има задача - да събира екипажи за пътувания. Всеки отбор трябва да включва трима души: командир, инженер и лекар. В същото време броят на специалистите в дадена област може да варира. Допустимо е например един лекар да бъде изпратен в две различни експедиции, тъй като има само двама лекари, а всеки командир и инженер може да има по трима. В този случай съставителят на експедиционния план трябва да вземе предвид психологическата съвместимост на членовете на екипа. Тази характеристика е една от най-важните в дългите и далечни експедиции за тяхното успешно поведение. Въз основа на всички описани условия се появява следната картина:
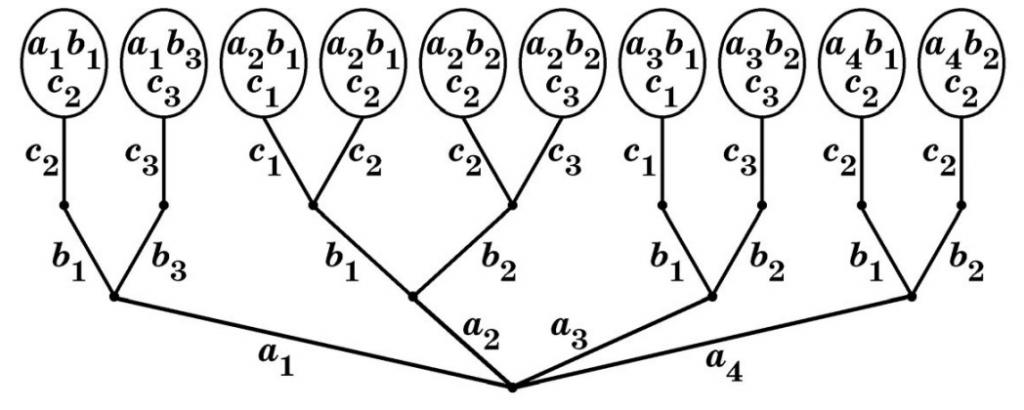
Където аз и са командирите, b i са инженерите и съм лекарите. В същото време, по време на тестването на всяко лице, се установи, че командирът а 1 психологически се разбира добре с инженери b 1 и b 3 , a 2 - с b 1 и b 2 , но лекарят c 3 е несъвместим с инженер b 1 и др. Въпросът, който първоначално беше зададен на ръководителя на проекта, беше колко екипажи могат да бъдат съставени при такива условия. От диаграмата може да се види, че може да има общо 10 такива екипажи, но какво би се случило, ако въпросът за психологическата съвместимост нямаше никакво тегло? Тогава се оказва, че след избора на командири a i , ще има 3 алтернативи за всеки от тях при избора на инженер. Съответно, за двама командири и инженери ще има и 3 варианта за лекари. Тогава броят на комбинациите ще достигне 4 * 3 * 3 = 36 екипажа.
Разположения, пермутации и комбинации
В примерите по-горе, решаването на проблемите възниква по т. Нар. Аксиоматичен метод. Това означава, че може да се каже, че съществуват редица основни задачи, решението на които може да се сведе до много проблеми. Както при стереометрията обаче, е неудобно да се решават проблеми, основани единствено на аксиоми, и за това се използва по-удобен инструмент, наречен „теореми“, така че в комбинаториката е по-удобно да се използват по-обобщени и доказани методи. В хода на вековното изучаване на комбинаториката стана ясно, че редица задачи се срещат по-често от други, а те се разделят на отделни класове и получават имената си, превръщайки се в основни комбинаторики - разположения, пермутации и комбинации.

Комбинаторни проблеми
Един от ключовите проблеми на комбинаторните методи е да се определи кой набор от задачи трябва да се разглежда комбинаторно. Това не може да бъде строго дефинирано поради изключително голямото разнообразие от проблеми, които попадат в комбинаторната категория. И тогава много задачи могат да се отнасят до комбинаториката, както и до друга област, която е съседна или гранична.

В опростения случай може да се отбележи, че комбинаторната математика включва проблеми, включващи проби и местоположения на обекти. В същото време комбинаториката се характеризира с работа изключително с ограничен набор от обекти. Въз основа на тези разпоредби можем да разграничим следните задачи, характерни за комбинаториката:
- Направете подбор на обекти, като вземете под внимание всички свойства.
- Докаже или опровергае съществуването на проба при определени условия.
- Намерете броя на възможните комбинации.
- Намерете всички комбинации и определете алгоритъма за тяхното изброяване.
- Намерете оптималното решение на даден проблем при определени условия.
Ако въпросният проблем може да бъде присвоен на един от тези типове, то той е комбиниран и комбинаторните формули ще помогнат за решаването му.