Структурна схема: примери, елементи, конструкция. Блок-схеми

В тази статия ще разгледаме примери на графики, които можете да срещнете в учебниците по компютърни науки и друга литература. Блок-схема е алгоритъм, който решава всяка задача, възложена на разработчика. Първо трябва да отговорите на въпроса какъв е алгоритъмът, как е представен графично, и най-важното, как да го решите, знаейки определени параметри. Трябва незабавно да се отбележи, че съществуват няколко вида алгоритми.

Какво е алгоритъм?

Тази дума е въведена в употреба от математика Мохамед ал-Хорезми, който е живял в периода от 763-850 година. Той е човекът, който е създал правилата за извършване на аритметични операции (има само четири). Но ГОСТ от 1974 г., който гласи:

Един алгоритъм е точно предписание, което определя един изчислителен процес. Освен това има няколко променливи с дадени стойности, които водят до изчисления до желания резултат.

Алгоритъмът ви позволява ясно да укажете на изпълнителя да изпълнява стриктно последователност от действия да разрешите проблема и да получите резултата. Разработването на алгоритъм е разпадането на една голяма задача в определена последователност от стъпки. Освен това, разработчикът на алгоритъма трябва да знае всички характеристики и правила за неговото създаване.

Характеристики на алгоритъма

Общо има осем характеристики на алгоритъма (независимо от неговия тип):

1. Има функция за въвеждане на първоначалните данни.
2. След завършване на алгоритъма има заключение за определен резултат. Трябва да се помни, че алгоритъмът е необходим, за да се постигне определена цел, а именно да се получи резултат, който е пряко свързан с изходните данни.
3. Алгоритъмът трябва да има структура от дискретен тип. Тя трябва да бъде представена в последователни стъпки. Освен това всяка следваща стъпка може да започне само след завършването на предишната.
4. Алгоритъмът трябва да бъде недвусмислен. Всяка стъпка е ясно определена и не позволява произволно тълкуване.
5. Алгоритъмът трябва да бъде ограничен - необходимо е той да бъде изпълнен в строго определен брой стъпки.
6. Алгоритъмът трябва да е правилен - да поиска само правилното решение на проблема.
7. Общността (или масов характер) - трябва да работи с различни източници на данни.
8. Времето за решаване на алгоритъма трябва да бъде минимално. Това определя ефективността на задачата.

И сега, знаейки какви алгоритми съществуват, можете да започнете да обмисляте как да ги напишете. И те не са много.

Вербален запис

Тази форма обикновено се използва, когато се описва процедурата за лице: „Отиди там, не знам къде. Донеси нещо, не знам какво.

Разбира се, това е комична форма, но същността е ясна. Например, например обичайният запис на прозорците на автобусите: „В случай на злополука извадете кабела, изстискайте стъклото“.

Тук условието е ясно определено, при което две действия трябва да бъдат изпълнени в строга последователност. Но това са най-простите алгоритми, има и по-сложни. Понякога се използват формули, специални обозначения, но при задължително условие - изпълнителят трябва да разбере всичко.

Разрешено е да се промени реда на действията, ако е необходимо да се върне, например, към предишната операция, или да се заобиколи някоя команда при определено условие. В същото време е желателно да се наберат екипите и да се посочи командата, към която се осъществява прехода: „След като приключите всички манипулации, повторете точки 3 до 5”.

Запис в графична форма

Този запис включва елементи на блок-схеми. Всички елементи са стандартизирани, всеки отбор има определен графичен запис. Специфична команда трябва да бъде записана във всеки един от блоковете в обикновен език или математически формули. Всички блокове трябва да бъдат свързани чрез линии - те показват точно какъв ред в изпълнените команди. Всъщност този тип алгоритъм е по-подходящ за използване в програмния код, отколкото за вербален.

Писане на езици за програмиране

В този случай, ако алгоритъмът е необходим за решаване на задачата с програма, инсталирана на компютър, тогава трябва да го напишете със специален код. За това има много езици за програмиране. И алгоритъмът в този случай се нарича програма.

Блок-схеми

Блок схемата е представяне на алгоритъма в графична форма. Всички екипи и действия са представени от геометрични форми (блокове). Във всяка фигура се вписва цялата информация за действията, които трябва да се извършат. Връзките се изобразяват като нормални линии със стрелки (ако е необходимо).

За проектирането на блок-схеми на алгоритми има ГОСТ 19.701-90. Той описва процедурата и правилата за тяхното създаване в графична форма, както и основните методи за решаване. В тази статия са представени основните елементи на блок-схемите, които се използват при решаването на проблеми, например в компютърните науки. И сега нека разгледаме правилата на строителството.

Основни правила за създаване на блок-схема

Има такива функции, които всяка блок-схема трябва да има:

1. Трябва да има два блока - "Старт" и "Край". И в едно копие.
2. От първоначалния блок до последната връзка трябва да се начертае.
3. От всички блокове, с изключение на последния, тръбопроводите трябва да изчезнат.
4. Трябва да има номерация на всички блокове: от горе до долу, от ляво на дясно. Последователният номер трябва да се постави в горния ляв ъгъл, като се направи пауза.
5. Всички блокове трябва да бъдат свързани помежду си по линии. Те трябва да определят последователността, с която се изпълняват действията. Ако потокът се движи нагоре или отдясно наляво (с други думи в обратен ред), стрелките се изтеглят.
6. Линиите са разделени на изходящи и входящи. Трябва да се отбележи, че един ред е за един изходящ блок, а за другия е входящ.
7. От първоначалния блок в схемата, поточната линия излиза само, тъй като тя е първата.
8. Но крайният блок има само вход. Това е ясно показано в примерите на графики, които са налични в статията.
9. За да се улесни четенето на графиките, входящите линии се изтеглят от по-горе и изходящите линии отдолу.
10. Наличието на пропуски в поточните линии. Те са задължително маркирани със специални конектори.
11. За да се улесни диаграмата, е позволено да се напише цялата информация в коментарите.

В таблицата са представени графични елементи на блок-схеми за решаване на алгоритми:

Алгоритми за линеен тип

Това е най-простата форма, която се състои от конкретна последователност от действия, те не зависят от първоначално въведените данни. Има няколко команди, които се изпълняват веднъж и само след като е направено предишното. Линейната блокова диаграма изглежда така:

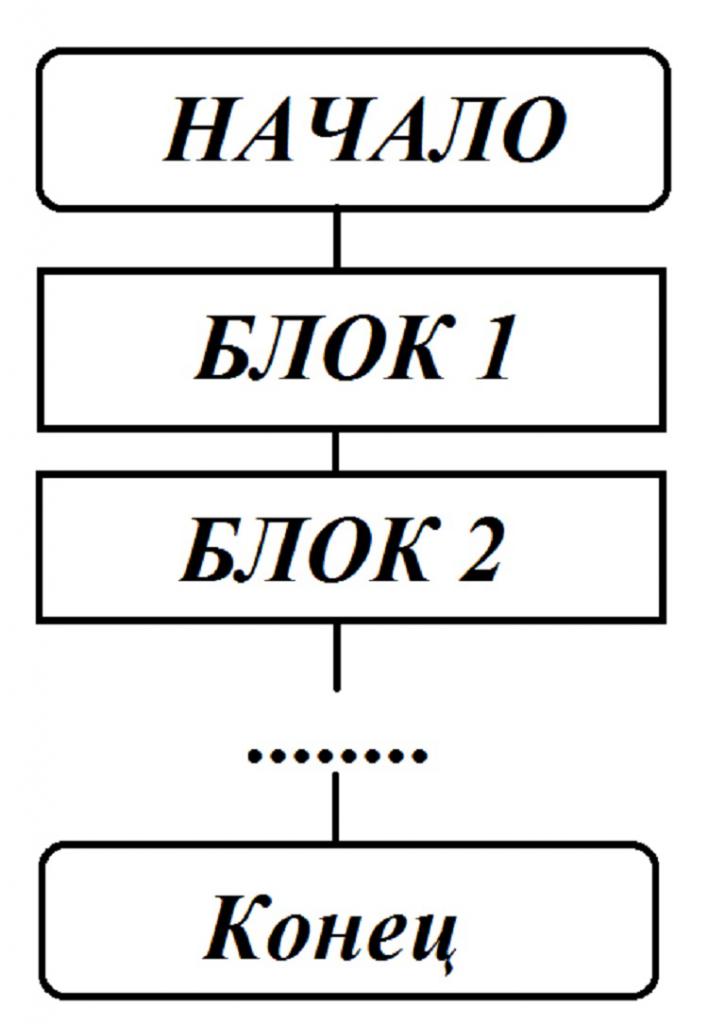
Освен това, връзките могат да вървят от горе до долу и от ляво на дясно. Такава блокова схема се използва за записване на изчислителните алгоритми, използвайки прости формули, които нямат ограничения върху стойностите на променливите, включени във формулите за изчислението. Линейният алгоритъм е неразделна част от сложните изчислителни процеси.

Алгоритми на разклоняване

Блок-схемите, базирани на такива алгоритми, са по-сложни от линейните. Но същността не се променя. Разклонителният алгоритъм е процес, при който по-нататъшното действие зависи от това как се изпълнява условието и какъв разтвор се получава. Всеки ред на действие е клон.

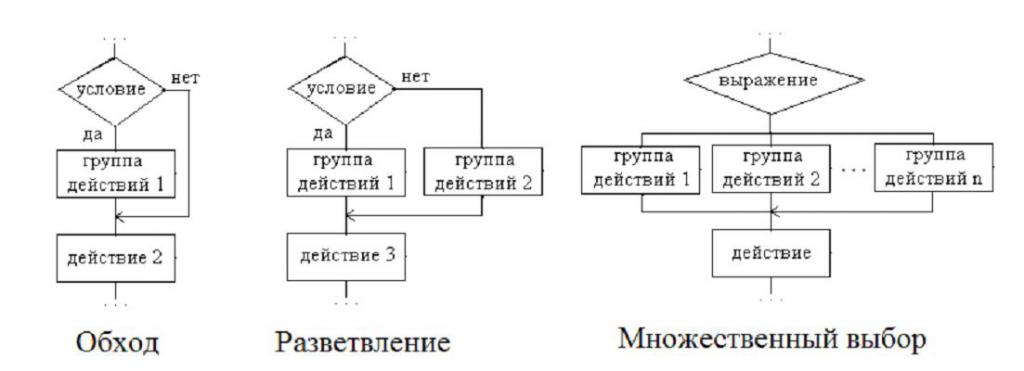
Диаграмите изобразяват блокове, които се наричат ​​"Решение". Той има два изхода и вътрешно е записано логическо условие. Именно от това как ще се изпълни, зависи по-нататъшното движение в схемата на алгоритъма. Можете да разделите алгоритмите на разклоняване на три групи:

1. “Bypass” - докато един от клоновете няма оператори. С други думи, няколко действия на друг клон са заобиколени.
2. "Разклоняване" - всеки клон има определен набор от изпълнени действия.
3. "Множествен избор" е разклонението, в което има няколко клона и всеки съдържа специфичен набор от действия, които трябва да бъдат изпълнени. И има една характеристика - изборът на посока директно зависи от това какви стойности са дадени за изразите, включени в алгоритъма.

Това са прости алгоритми, които се решават много просто. Сега да преминем към по-сложни.

Цикличен алгоритъм

Тук всичко е много ясно - цикличната блокова диаграма представлява алгоритъм, при който хомогенните изчисления се повтарят многократно. По дефиниция, цикълът е специфична последователност от действия, които се изпълняват многократно (повече от веднъж). Има няколко вида цикли:

1. Кой знае броя на повторенията на действията (те се наричат ​​още цикли с брояч).
2. В които броят на повторенията е неизвестен - с пост-условие и предварително условие.

Независимо от вида на цикъла, който се използва за решаване на алгоритъма, той трябва да има променлива, с която се получава изхода. Той определя броя на повторенията на цикъла. Работната част (тялото) на цикъла е специфична последователност от действия, която се изпълнява на всяка стъпка. И сега ще разгледаме по-отблизо всички видове цикли, които могат да възникнат при изработването на алгоритми и решаване на проблемите на компютърните науки.

Брояч цикли

На фигурата е показана проста блокова схема, в която има цикъл с брояч. Този тип алгоритъм показва, че броят на повторенията на даден цикъл е известен предварително. И този номер е фиксиран. В този случай, променливата, броят на стъпките (повторения) се нарича брояч. Понякога в учебниците може да попаднете на други дефиниции - цикъл параметър, контролна променлива.

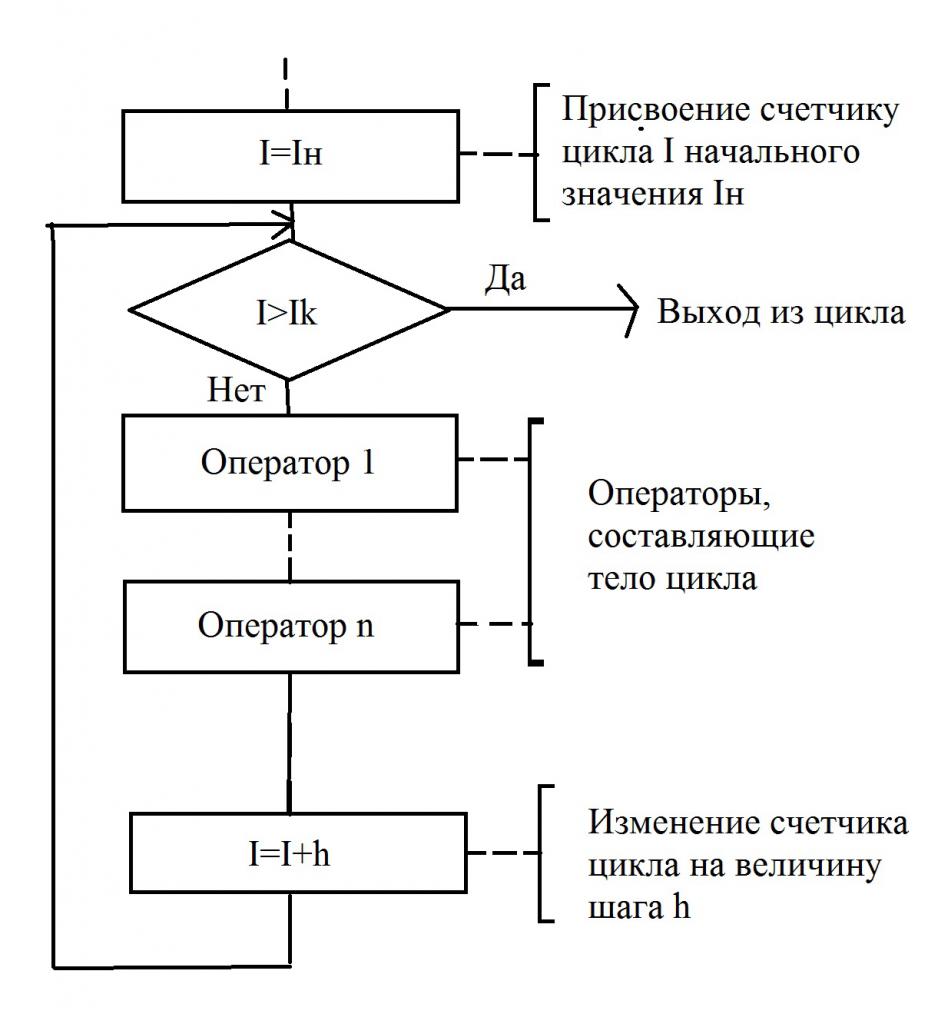
Блок-схемата илюстрира много ясно как работи цикъла с брояча. Преди да пристъпите към първата стъпка, трябва да зададете начална стойност на брояча - тя може да бъде произволно число, зависи от конкретния алгоритъм. В случая, когато крайната стойност е по-малка от стойността на брояча, ще бъде изпълнена определена група команди, които съставляват тялото на цикъла.

След като тялото е изпълнено, броячът се променя от стойността на прираста на брояча, обозначена с буквата h. В случай, че получената стойност е по-малка от крайната, цикълът ще продължи. И ще свърши само когато крайната стойност е по-малка от брояча на цикъла. Само в този случай ще се изпълни действието, което следва цикъла.

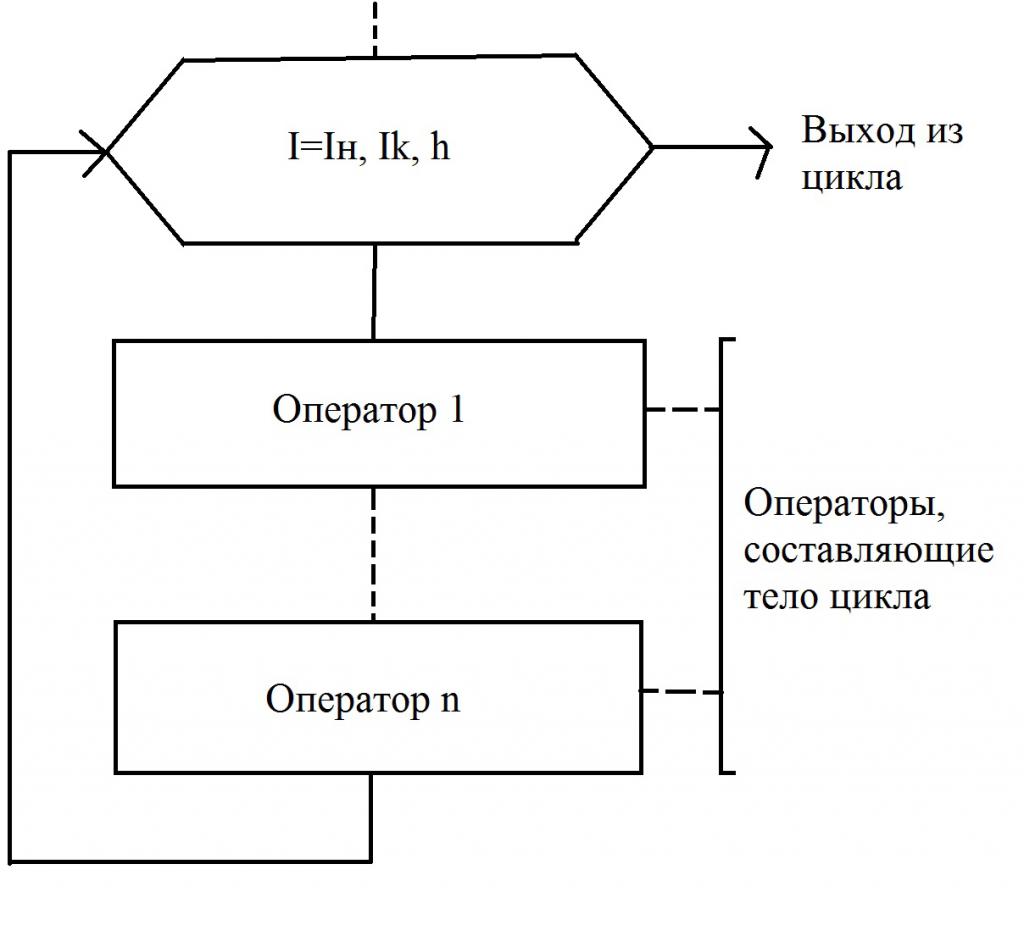
Обикновено в блок-схемата се използва блок, наречен "Подготовка". Той се записва в брояча и след това се посочват следните данни: началната и крайната стойност, стъпката се променя. В блоковата диаграма това са параметрите I n, Ik и h, съответно. В случая, когато h = 1, размерът на стъпката не се записва. В други случаи това трябва да се направи. Необходимо е да се придържате към просто правило - поточната линия трябва да влиза от горе. И поточната линия, която отива под (или надясно, в зависимост от конкретния алгоритъм), трябва да показва прехода към следващия оператор.

Сега сте напълно проучили описанието на диаграмата, показана на фигурата. Можете да продължите към по-нататъшно проучване. Когато се използва цикъл с брояч, трябва да бъдат изпълнени някои условия:

1. На тялото не е позволено да променя (насилствено) стойността на брояча.
2. Забранено е да се прехвърля контрол отвън на оператора на тялото. С други думи, човек може да влезе в цикъла само от самото начало.

Предварителни условия

Този тип цикли се използват в случаите, когато броят на повторенията не е известен предварително. Цикъл с предварително условие е тип алгоритъм, в който непосредствено преди тялото да започне да изпълнява, той проверява състоянието, при което е разрешен преходът към следващото действие. Забележете как са изобразени елементите на блоковата диаграма.

В случай, че условието е изпълнено (изявлението е вярно), настъпва преход към началото на цикъла. Той директно променя стойността на поне една променлива, която влияе на стойността на зададеното условие. Ако не се придържате към това правило, ние получаваме "цикъл". В случай, че след следващата проверка на състоянието на изпълнение на тялото на цикъла, се окаже, че е невярно, тогава настъпва изход.

В блоковете на алгоритмите е позволено да се провери не истината, а фалшивостта на първоначалното състояние. В този случай цикълът ще излезе само ако стойността на условието е вярна. И двата варианта са правилни, тяхната употреба зависи от това какво конкретно е по-удобно да се използва за решаване на конкретен проблем. Този тип цикъл има една характеристика - тялото не може да бъде изпълнено, когато условието е невярно или вярно (в зависимост от варианта, който се използва за решаване на алгоритъма).

По-долу е представена блок-схема, която описва всички тези действия:

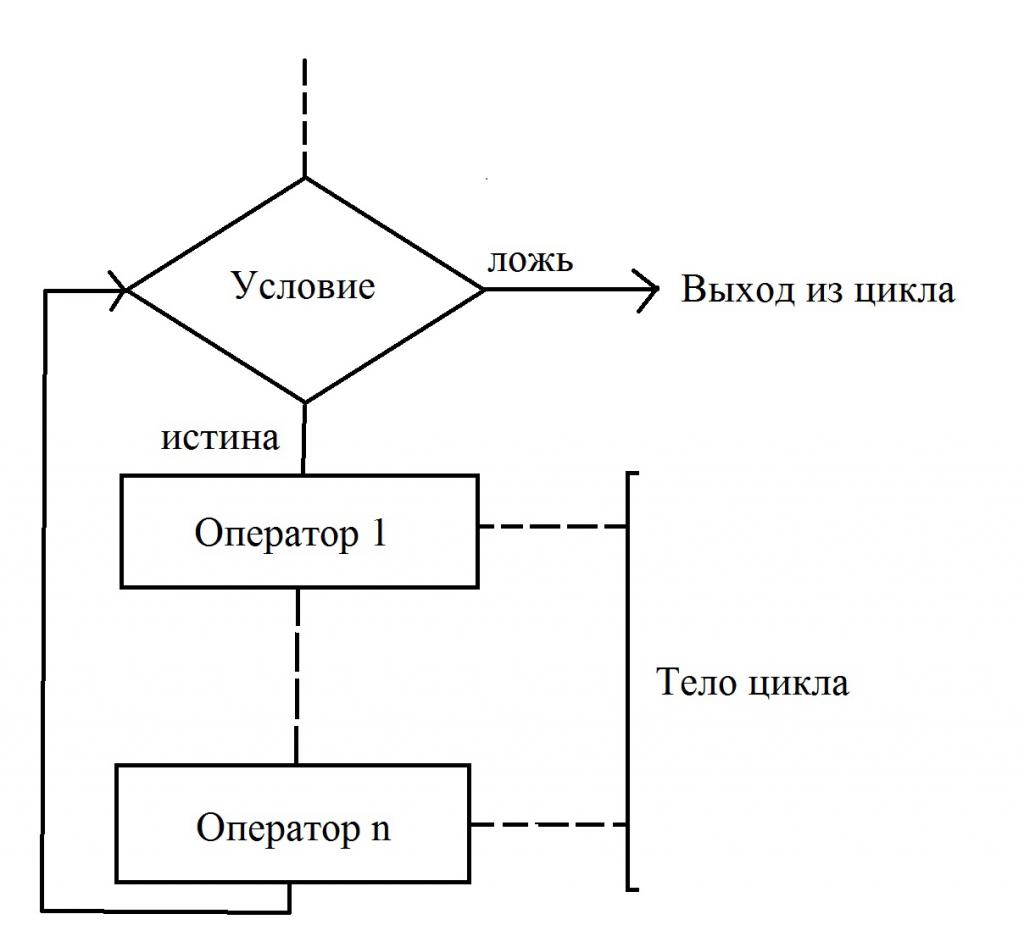
Какво е цикъл с последващо условие?

Ако се вгледате внимателно, тогава този вид цикли е донякъде подобен на предишния. Ще се опитаме да изградим блок-схема, описваща този цикъл самостоятелно. Особеност е, че броят на повторенията не е известен предварително. И състоянието е поставено след оттеглянето от тялото. Това показва, че органът, независимо от решението, ще бъде изпълнен поне веднъж. За по-голяма яснота разгледайте блок-схемата, описваща състоянието и изявленията:

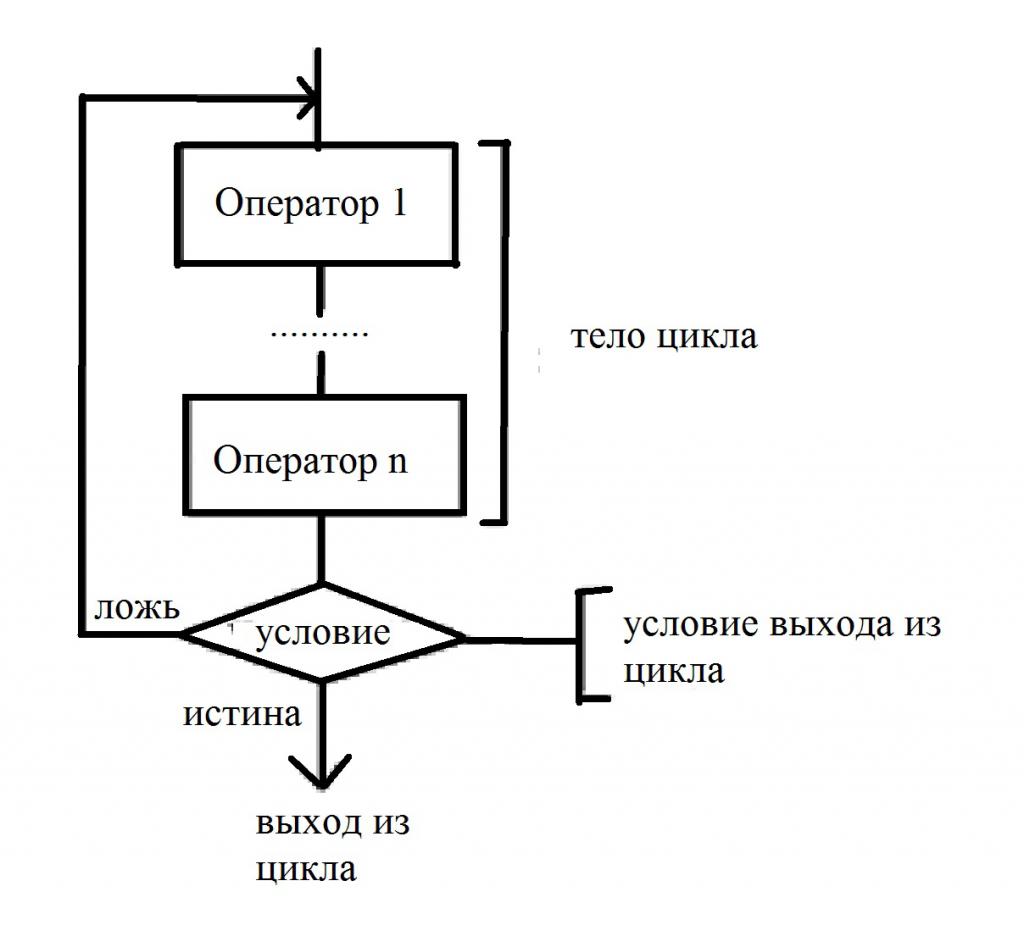
Няма нищо трудно в изграждането на алгоритми с цикли, достатъчно е да ги разберем само веднъж. И сега се обръщаме към по-сложни структури.

Сложни цикли

Комплексни са тези конструкции, в които има един или повече прости цикли. Понякога те се наричат ​​вложени. В същото време тези структури, които покриват други цикли, се наричат ​​„външни“. И тези, които са включени в дизайна на външните - вътрешни. Когато се изпълнява всяка стъпка от външния контур, вътрешният контур се превърта напълно, както е показано на фигурата:

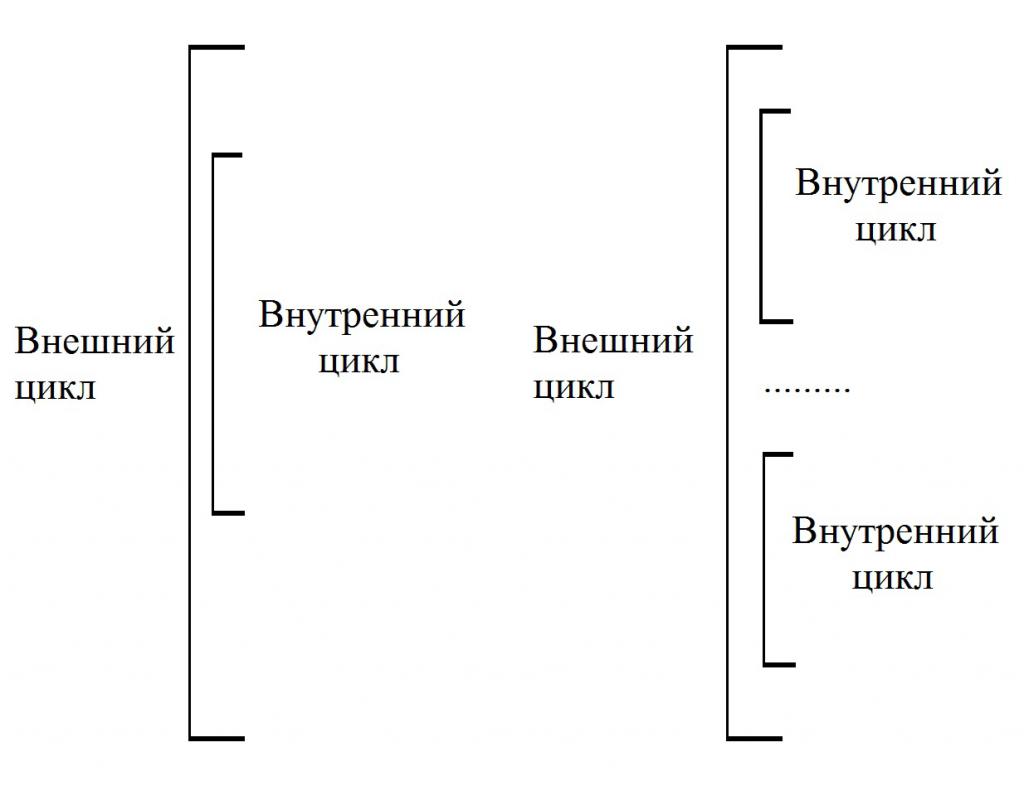
Това е всичко, прегледахте основните характеристики на изграждането на блок-схеми за решаване на алгоритми, знаете принципите и правилата. Сега можете да обмислите конкретни примери на графики от живота. Например, в психологията такива конструкции се използват, за да може човек да реши въпрос:

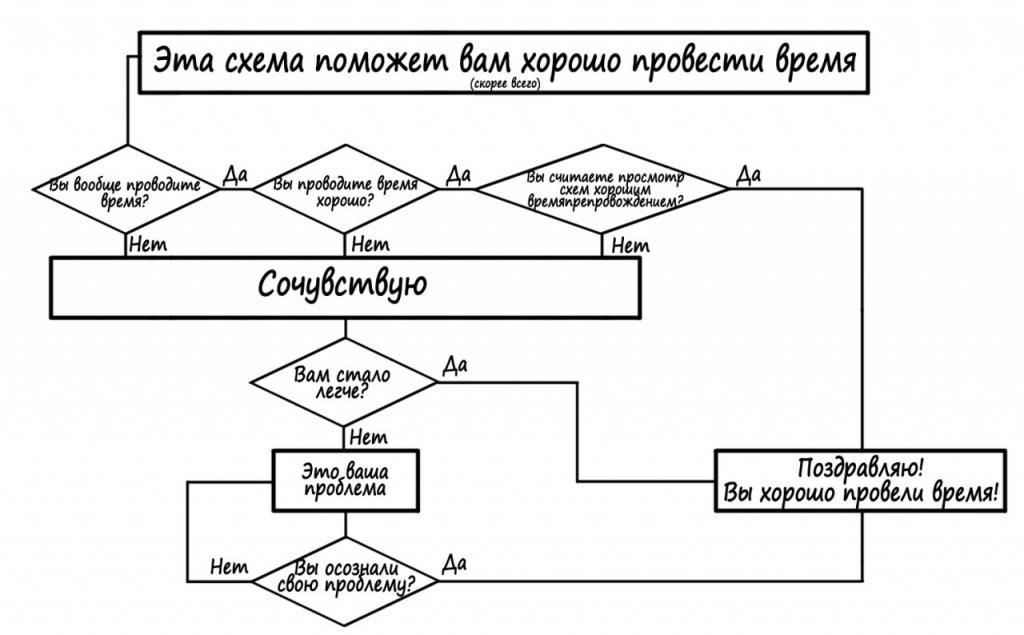
Или пример от биология за решаване на проблема:

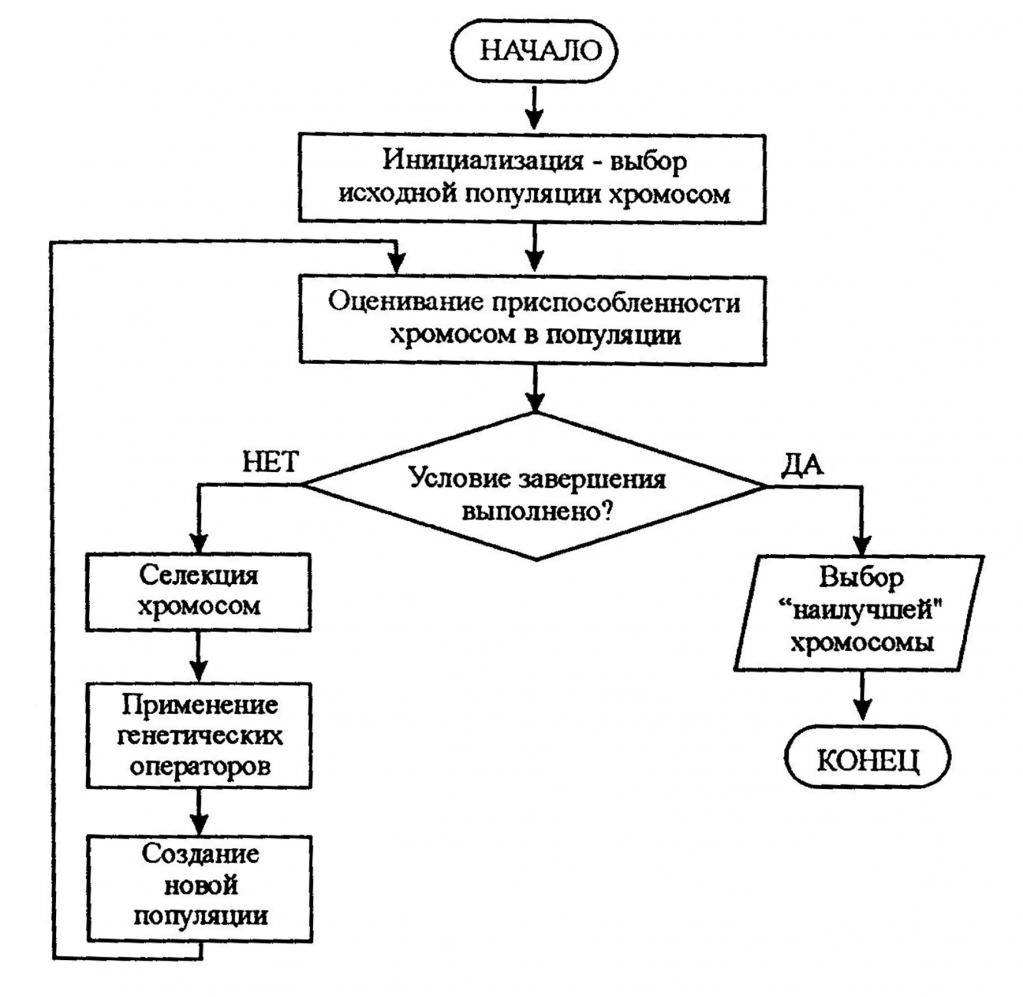
Решаване на проблеми с блок-схеми

Сега ще разгледаме примери за проблеми с блок-схеми, които могат да бъдат намерени в учебниците по компютърни науки. Например, дадена е блокова диаграма, според която се решава алгоритъм:

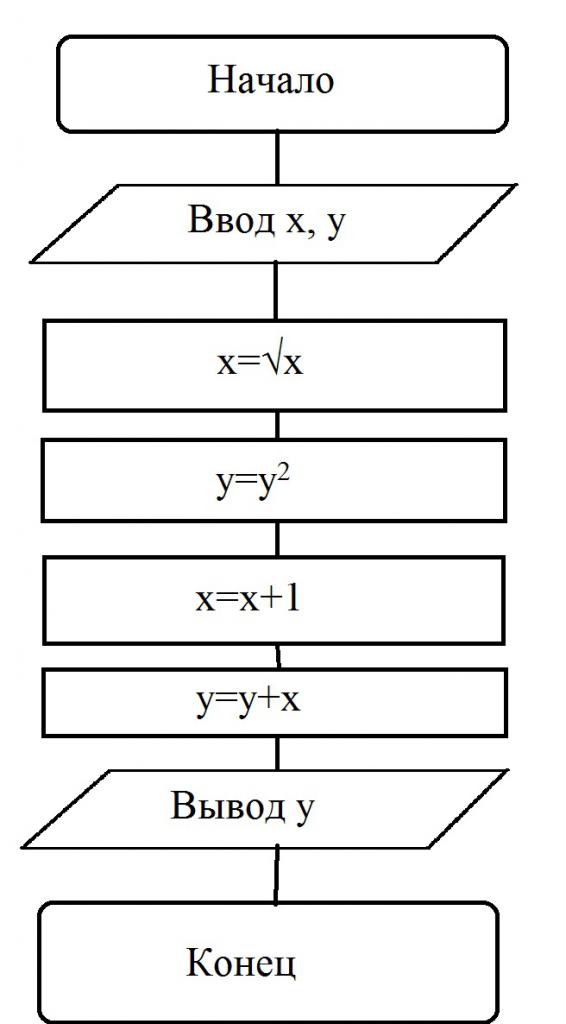
В този случай потребителят самостоятелно въвежда стойностите на променливите. Да предположим, че x = 16 и y = 2. Процесът на това:

1. Въвеждат се стойностите на x и y.
2. Операцията по преобразуване се извършва: x = =16 = 4.
3. Условието е изпълнено: y = y ² = 4.
4. Изчислението се извършва: x = (x + 1) = (4 + 1) = 5.
5. Следващата променлива се изчислява допълнително: y = (y + x) = (5 + 4) = 9.
6. Решението се показва: y = 9.

В този пример графиките за компютърни науки ясно показват как е решен алгоритъмът. Трябва да обърнете внимание на факта, че стойностите на x и y са поставени на началния етап и те могат да бъдат всичко.