Основни понятия от теория на вероятностите и математическа статистика

Математиката включва цял набор от области, една от които, заедно с алгебрата и геометрията, е теория на вероятностите. Има термини, които са общи за всички тези области, но освен тях има и специфични, специфични само за една конкретна "ниша" думи, формули, теореми.

Фразата "теория на вероятностите" предизвиква паника в неподготвен ученик. Всъщност, въображението рисува картини, където се появяват ужасни обемни формули, а решението на един проблем заема цял тетрадка. На практика обаче нещата не са толкова ужасни: достатъчно е веднъж да се разбере смисъла на някои термини и да се стигне до същността на някаква особена логика на разсъжденията, за да се спре да се страхуваш веднъж завинаги. В тази връзка разглеждаме основните понятия на теорията на вероятностите и математическата статистика - млада, но изключително интересна област на знанието.

Защо да преподаваме понятия

Функцията на езика е да предава информация от един човек на друг, така че той да го разбира, осъзнава и може да го използва. Всяка математическа концепция може да се обясни с прости думи, но в този случай обменът на данни ще отнеме много повече време. Представете си, че вместо думата "хипотенуза" винаги ще трябва да кажете "най-дългата страна на правилния триъгълник" - това е изключително неудобно и дълго.

Затова хората измислят нови термини за определени явления и процеси. По същия начин се появяват основните понятия на теорията на вероятностите - събитието, вероятността за събитие и т.н. Така че, за да се използват формули, да се решават проблеми и да се прилагат умения в живота, е необходимо не само да се запомнят нови думи, но и да се разбере какво означава всеки от тях. Колкото по-дълбоко осъзнавате тях, потъвате в смисъла, толкова по-широк е обхватът на вашите възможности и колкото по-пълно възприемате света около вас.

Какъв е смисълът на субекта

Да се ​​запознаем с основните понятия на теорията на вероятностите. Класическата дефиниция на вероятността е следната: това е съотношението на резултатите, които отговарят на изследователя към общия брой възможни. Нека дадем един прост пример: когато човек навие умре, той може да пусне всяка от шестте страни нагоре. Така общият брой на резултатите е шест. Вероятността за случайно избрано отпадане на страната е 1/6.

Възможността да се предвиди появата на конкретен резултат е изключително важна за различни специалисти. Колко дефектни части се очакват много? Зависи от това колко да се произведе. Каква е вероятността лекарството да помогне за борбата с болестта? Тази информация е жизненоважна. Но да не губим време за допълнителни примери и да продължим да изучаваме нова област за нас.

Първо запознанство

Разгледайте основните понятия на теорията на вероятностите и тяхното използване. Най- право естествено Науките, икономическите формули и термините, представени по-долу, се използват навсякъде, тъй като те са пряко свързани със статистическите данни и грешките в измерването. По-подробно проучване на този въпрос ще ви отвори нови формули, които са полезни за по-точни и сложни изчисления, но нека започнем с едно просто.

Една от най-основните и основни понятия на теорията на вероятностите и математическата статистика е случайно събитие. Обяснете с ясни думи: от всички възможни резултати от експеримента, само един се наблюдава като резултат. Дори ако вероятността за настъпване на това събитие е много по-висока от другата, тя ще бъде случайна, тъй като теоретично резултатът би могъл да бъде различен.

Ако проведохме серия от експерименти и получихме определен брой резултати, тогава вероятността за всяка от тях се изчислява по формулата: P (A) = m / n. Тук m е колко пъти в тестовите серии сме виждали резултата от интерес за нас. На свой ред n е общият брой проведени експерименти. Ако сме хвърлили монета 10 пъти и получихме "опашки" 5 пъти, тогава m = 5 и n = 10.

Видове събития

Случва се, че някакъв резултат е гарантиран за всеки опит - подобно събитие ще се нарече надеждно. Ако това никога не се случи, то ще бъде наречено невъзможно. Такива събития обаче не се използват в условията на проблеми по теория на вероятностите. Основните понятия, които са много по-важни за познаване, са съвместни и несъвместими събития.

Случва се, че по време на експеримента се случват едновременно две събития. Например, хвърляме две зарчета - в този случай фактът, че някой е имал „шест“, не гарантира, че вторият няма да падне на втория. Такива събития ще се наричат ​​съвместни.

Ако преобърнем една смърт, тогава две числа едновременно няма да могат да изпаднат. В този случай резултатите под формата на изпуснати „едно“, „две“ и т.н. ще се считат за несъвместими събития. Много е важно да се разграничат резултатите, които се случват във всеки конкретен случай - зависи от това кои формули да се използват в проблема за намиране на вероятности. Основните понятия на теорията на вероятностите, ще продължим да изучаваме няколко параграфа по-късно, когато разгледаме особеностите на добавянето и умножението. Всъщност, без тях не може да бъде решен никакъв проблем.

Количество и продукт

Да предположим, че навивате умре с приятел и той има „четири“. Трябва да спечелите пет или шест. В този случай вероятностите ще се сумират: тъй като шансовете за отпадане на двата числа са 1/6, отговорът ще изглежда като 1/6 + 1/6 = 1/3.

Сега си представете, че вие ​​навивате умират два пъти и приятелят ви е получил 11 точки. Сега трябва да имате “шест” два пъти подред. Събитията са независими един от друг, така че вероятността трябва да се умножи: 1/6 * 1/6 = 1/36.

Сред основните понятия и теореми на теорията на вероятностите трябва да се обърне внимание на сумата от вероятностите за съвместни събития, t. това е, което може да се случи едновременно. Формулата на добавянето в този случай ще изглежда така: P (A + B) = P (A) + P (B) - P (AB).

комбинаторика

Много често трябва да намерим всички възможни комбинации от някои параметри на обекта или да изчислим броя на всякакви комбинации (например при избора на шифър). Комбинаториката, която е тясно свързана с теорията на вероятността, ще ни помогне в това. Основните понятия тук включват някои нови думи и редица формули от тази тема със сигурност ще дойдат.

Да предположим, че имате три числа: 1, 2, 3. Трябва да ги използвате, за да напишете всички възможни трицифрени числа. Колко ще има? Отговор: n! (удивителен знак означава факториал). Комбинациите от множество различни елементи (числа, букви и т.н.), които се различават само по реда на тяхното местоположение, се наричат ​​пермутации.

Въпреки това, по-често се сблъскваме с такава ситуация: има 10 цифри (от нула до девет), от които е съставена паролата или кода. Да предположим, че дължината му е 4 знака. Как да изчислим общия брой възможни кодове? За това съществува специална формула: (n!) / (N - m)!

Като се има предвид предложеното условие за проблем, n = 10, m = 4. Освен това са необходими само прости математически изчисления. Между другото, такива комбинации ще се наричат ​​поставяне.

И накрая, има концепция за комбинации - това са последователности, които се различават един от друг поне с един елемент. Техният брой се изчислява по формулата: (n!) / (M! (Nm)!).

Математически очаквания

Важна концепция, която студентът среща още в първите класове по темата, е математическото очакване. Това е сумата от всички възможни стойности на резултата, умножени по техните вероятности. По същество, това е среден брой, който можем да предвидим като резултат от теста. Например, има три стойности, за които вероятностите са показани в скоби: 0 (0,2); 1 (0.5); 2 (0.3). Изчислете очакването: M (X) = 0 * 0.2 + 1 * 0.5 + 2 * 0.3 = 1.1. Така от предложената формулировка можем да видим, че тази стойност е постоянна и не зависи от резултата от теста.

Тази концепция се използва в много формули, а вие ще я намирате многократно в бъдеще. Лесно е да се работи с него: очакването на сумата е равно на сумата на таблата. очаквания - M (X + Y) = M (X) + M (Y). Същото се отнася и за продукта: M (XY) = M (X) * M (Y).

дисперсия

Трябва да е от курса по физика в училище, за който помните, че дисперсията се разсейва. Какво е мястото му сред основните понятия на теорията на вероятностите?

Вижте два примера. В един случай ни се дава: 10 (0,2); 20 (0.6); 30 (0.2). В другия - 0 (0,2); 20 (0.6); 40 (0.2). Математическото очакване в двата случая ще бъде същото, така че как можем да сравним тези ситуации? Все пак виждаме с просто око, че разпространението на стойностите във втория случай е много по-голямо.

За тази цел беше въведена концепцията за дисперсията. За да го получите, трябва да изчислите очакването на сумата от разликите на всяка случайна променлива и очакването. Вземете числата от първия пример, записан в предишния параграф.

Първо изчисляваме очакването: M (X) = 10 * 0.2 + 20 * 0.6 + 30 * 0.2 = 20. Тогава стойността на дисперсията: D (X) = 40.

Друго от основните понятия на статистиката и теорията на вероятността е стандартното отклонение. Изчислете, че е много проста: просто трябва да вземете квадратен корен от дисперсията.

Тук можем да отбележим толкова просто понятие, колкото обхвата. Тази стойност показва разликата между максималните и минималните стойности в извадката.

статистика

Някои основни училищни концепции се използват в науката много често. Две от тях са средно аритметично и средно. Със сигурност си спомняте как да намерите техните ценности. Но за всеки случай си спомняме: средната аритметична стойност е сумата от всички стойности, разделени на техния брой. Ако стойността е 10, след това ги добавяме и разделяме на 10.

Медианата е централна за всички възможни. Ако имаме нечетен брой стойности, тогава ги записваме във възходящ ред и избираме този, който е в средата. Ако имаме четен брой стойности, ще вземем две централни и ще разделим на две.

Още две стойности, разположени между медианата и двете крайни - максимални и минимални - стойности на множеството, се наричат ​​квартили. Те се изчисляват по същия начин - с нечетен брой елементи се взема число, което се намира в средата на един ред, а за четни - половината от сумата на два централни елемента.

Има и специална графика, в която можете да видите всички стойности на извадката, нейния обхват, медиана, интервал между тримесечия и емисии - стойности, които не се вписват в статистическата грешка. Полученото изображение има много специфично (и дори не-математическо) име - кутия с мустаци.

разпределение

Разпределението се отнася и до основните понятия на теорията на вероятностите и математическата статистика. Накратко, това е резюме на всички случайни променливи, които можем да видим в резултат на теста. Основният параметър тук е вероятността от възникване на всяка конкретна стойност.

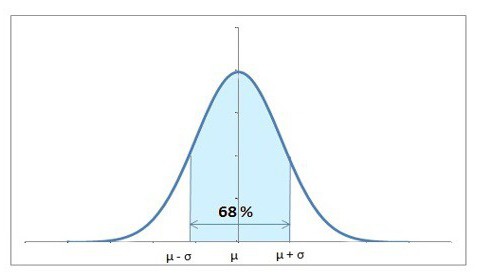Нормално разпределение е това, което има един централен връх, в който се намира най-често срещаната стойност. От него дъгите се различават все по-малко вероятно. Като цяло, графикът от страна изглежда като "слайд". В бъдеще ще научите, че централната гранична теорема, която е фундаментална за теорията на вероятностите, е тясно свързана с този тип разпределение. Той описва законите, които са важни за разглежданите от нас клонове на математиката, които са много полезни за различни изчисления.

Но обратно към темата. Има още два вида разпределения: асиметрични и мултимодални. Първата изглежда като половината от "нормалната" графика, т.е. дъгата се спуска само в една посока от пиковата стойност. Накрая, мултимодалното разпределение е такова, че има няколко „горни” стойности. Графикът, следователно, пада, след това се издига. Най-честотната стойност във всяка дистрибуция се нарича режим. Това е и една от основните концепции на теорията на вероятностите и математическата статистика.

Гаусово разпределение

Гаусово или нормално разпределение е такова, в което отклонението на наблюденията от средното се подчинява на определен закон.

Накратко, основният разпръснатост на извадковите стойности има тенденция към режима - най-често срещаният от тях. Да говорим по-точно, тогава 99.6% от всички стойности са в рамките на три стандартни отклонения (не забравяйте, че разглеждахме това понятие по-горе?).

Гаусовото разпределение е една от основните концепции на теорията на вероятностите. С негова помощ е възможно да се разбере дали даден елемент е включен в категорията „типичен” според един или друг параметър - това е начинът, по който височината и теглото на човек се оценяват според възрастта, нивото на интелектуално развитие, психологическото състояние и много други.

Как да кандидатствате

Интересното е, че „скучните“ математически данни могат да бъдат използвани в своя полза. Например, един млад мъж прилага теория на вероятностите и статистика, за да спечели няколко милиона долара в рулетка. Вярно е, че трябваше да се подготвим за това - в продължение на няколко месеца записахме резултатите от игрите в различни казина.

След анализа той откри, че една от таблиците е леко наклонена, което означава, че редица стойности се появяват статистически значително по-често от други. Малко изчисление, търпение - и сега собствениците на институцията са озадачени, мислейки как човек може да получи толкова късмет.

Има много ежедневни ежедневни задачи, които не могат да бъдат решени, без да се прибягва до статистика. Например, как да се определи колко магазин да поръчате дрехи с различни размери: S, M, L, XL? За да направите това, е необходимо да се анализира кой често купува дрехи в града, в района, в близки магазини. Ако такава информация не бъде получена, собственикът рискува да загуби много пари.

заключение

Разгледахме цял набор от основни понятия от теорията на вероятностите: тест, събитие, пермутации и разположения, очакване и дисперсия, мода и нормално разпределение ... Освен това изследвахме редица формули, които повече от един месец изследване бяха посветени на изучаването на които.

Не забравяйте: математиката е необходима при изучаване на икономика, естествени науки, информационни технологии, инженерни специалности. Статистиката като една от областите тук също не може да бъде избегната.

Сега зависи от вас: практика, решаване на проблеми и примери. Дори основните понятия и дефиниции на теорията на вероятността ще бъдат забравени, ако не и да се отделя време за повторение. Освен това следващите формули в голяма степен ще разчитат на тези, които сме разгледали. Затова се опитайте да ги запомните, особено след като не са толкова много.