Алгебрична прогресия: формули и примери за решения
Тази статия ще обсъди алгебричната прогресия, формулите, необходими за решаването на проблеми с нейното участие, както и някои примери за тяхното използване. За пълнота ще говорим накратко за друг вид прогресия - геометрична.
Концепцията за алгебрична прогресия

Всяка поредица от числа, която е подредена по някакъв закон, може да се нарече прогресия. Най-популярни и използвани за решаване на практически задачи са два вида такива серии: алгебрична и геометрична прогресия. Разгледайте първия от тях по-подробно.
Алгебричната често се нарича аритметична прогресия. Математически, това означава следното:
a n = a n-1 + d
Тоест, говорим за такава цифрова последователност, в която всеки от неговите членове се различава от предишния или следващия със същия номер d. Този номер се нарича разлика (може да се определи чрез намиране на разликата между два съседни елемента на прогресията).
Според тази дефиниция, разглежданата прогресия има начало, но не и край. Той винаги започва с термина a 1 (всяко реално число) и след това продължава със сумиране на този член с разликата d. Съответно, тя може да бъде безкрайно нарастваща (d> 0) или намаляваща (d <0). Ситуацията, когато d = 0 може да се разглежда и като специален случай на аритметична прогресия, представена от безкрайна последователност от еднакви числа.
Формула за намиране на произволен член
Както беше обяснено по-горе, разглежданият тип прогресия е уникално определен от първия си елемент и разликата, но това правило се прилага за всички други стойности. Например, познаването на два произволни елемента или един елемент и сумата на определен брой членове също определя уникално прогресията.
За да изчислите n-тия елемент, можете успешно да използвате следната формула:
a n = a 1 + (n - 1) * d
Очевидността на валидността на този израз е без съмнение и всеки може да го провери, като замени малките стойности на n.
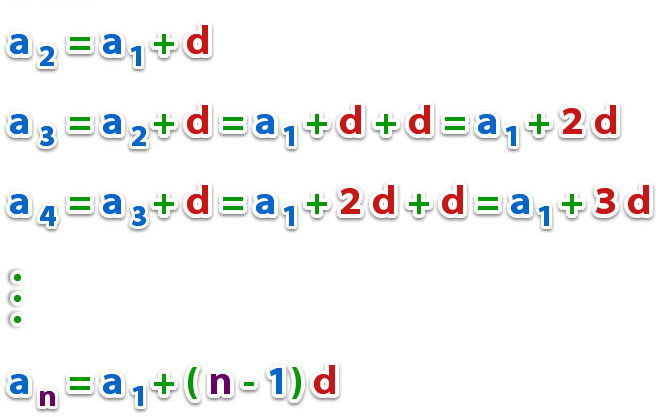
Формула за възстановяване на прогресията на два известни елемента
В училищния курс по алгебра такива проблеми са типични за една прогресия: има два елемента a n и a m , а n> m, необходимо е да се изгради цялата прогресия върху тях.
Този проблем се решава с помощта на формулата за n-тия член. Изписваме две съответни изрази:
a n = a 1 + (n - 1) * d;
a m = a 1 + (m - 1) * d
Намерете разликата между първия и втория (знакът за равенство е запазен):
a n - a m = (n - m) * d =>
d = (a n - a m ) / (n - m)
Виждаме колко лесно е да се намери разликата в прогресията, ако са известни две от неговите членове: за да се направи това, извадете по-малката от по-голямата по ред и след това разделете получената разлика с разликата в техните последователни номера.
След като се намери разликата, е лесно да се изчисли първият термин (за да направите това, използвайте някоя от първите две изрази).
Сумата на алгебричната прогресия
Друга серия от типични задачи за прогресия е намирането на сумата на техните членове. Следната формула е алгебрична сума на прогресията:
S n = ∑ i = 1 n (a i ) = n * (a 1 + a n ) / 2
Това означава, че за да се определи сумата на първите членове на n, трябва да се изчисли сумата от само две от тях (първата и n-тата), да се умножи по броя на членовете n и да се раздели полученото.
Пропускаме математическото доказателство за този израз, но все пак даваме логично доказателство. Може да се отбележи, че с оглед на свойството на разглеждания тип прогресия, винаги има следното равенство:
a 1 + a n = a 2 + a n-1
Всъщност, вторият член е по-голям от първия член с d, но със същото предпоследно (a n-1 ) е по-малък от последния ( n ). В случай на двойка елементи получаваме точно половината от тези суми от общия брой елементи (n / 2), откъдето следва редуцираната формула за S n .

Смята се, че забелязаната черта на аритметичната прогресия е създадена от Карл Гаус, известен математик от края на XVIII - първата половина на XIX век, когато в съзнанието си за няколко секунди изчислява сумата на естествените числа от 1 до 100.
Примери за решаване на проблеми
Разгледайте два примера за алгебрична прогресия.
1. Известно е, че 9-ият срок е 7, а 21-ият е 51. Необходимо е да се намерят първите 5 члена на тази аритметична прогресия.
Условието на задачата позволява да се изчисли веднага разликата d, прилагайки формулата с n и a m , която е написана по-горе. Имаме:
d = (a n - a m ) / (n - m) = (51 - 7) / (21 - 9) = 3,667
След получаване на разликата d, ние извършихме закръгляване до 3 знака след десетичната запетая.
Сега можете да изчислите първия елемент от серията. За да направите това, използвайте данните за 9 члена:
a 9 = a 1 + d * 8 => a 1 = a 9 - d * 8 = 7 - 3,667 * 8 = -22,336
За да решите проблема, остава да направите последната стъпка: добавете последователно 4 пъти стойността на d към първия елемент. Получаваме:
a 1 = -22,336;
a2 = -22,336 + 3,667 = -18,669;
a3 = -18.669 + 3.677 = -15.002;
a 4 = -15,002 + 3,667 = -11,335;
a 5 = -11,335 + 3,667 = -7,668
Припомнете си, че всички изчислени стойности са валидни до третия знак след десетичната запетая.
2. Работниците сгънали дървени трупи във формата на пирамида. Известно е, че те са поставили само 33 трупа и само 3 трупа са изчезнали до края на пирамидата. Необходимо е да се определи колко редове дървени трупи поставени работници.
Отговорът на този въпрос е да се реши алгебричната прогресия, но за да се пристъпи към нея, трябва внимателно да се справим с това състояние.
Първо, тъй като дървесните трупи се прибавят към пирамидата, това означава, че във всеки предишен ред е имало още един дневник, т.е. празно:
a 1 = 1, a 2 = a 1 + d = 2, a 1 + a 2 = 3
Ние вземаме под внимание тези три журнала, като ги добавяме към вече сгънатите 33 и определяме неизвестния брой редове n, като използваме формулите за сумата и n-тия член:
S n = n * (a 1 + a n ) / 2; a n = a 1 + d * (n - 1) =>
S n = n * (a 1 + a 1 + d * (n - 1)) / 2 = (2 * a 1 - d) / 2 * n + d * n 2/2
Подменим известните данни в последното равенство и решим полученото квадратично уравнение за п:
36 = 0.5 * n + 0.5 * n2 или
n 2 + n - 72 = 0
Дискриминант: D = 1 - 4 * 1 * (-72) = 289
Корени: n = (-1 ± 17) / 2 = (8; -9)
Ще отхвърлим негативната стойност веднага, тъй като тя противоречи на състоянието на проблема. Така 8-те реда на пирамидата ще съдържат 36 дневници. Тъй като работниците не са завършили двата горни реда, това означава, че те са събрали само 6 реда дървени трупи.
Няколко думи за развитието на геометричното
Алгебричната и геометричната прогресия, като правило, се разглеждат в рамките на една тема, затова е полезно да се даде представа за втория тип подредени поредни номера. Така че, геометричната прогресия е поредица от числа, които се подчиняват на закона:
a n = a n-1 * r
Това означава, че за разлика от аритметиката, тук, за да получим всички елементи, не трябва да добавяме едно число, а да го умножаваме (r се нарича знаменател).
От дефиницията е ясно, че геометричната прогресия нараства (намалява) много по-бързо от аритметичната.
Той често се използва в геометрията, например, когато се изчисляват площите на цифрите, като се използва тяхното разделяне на отделни елементи (методът на разделяне на половина).