Каква е силата на азбуката
Азбуката в компютърните науки е знаковата система, с която можете да подадете информационно съобщение. За да разберем същността на това определение, ето някои допълнителни теоретични факти:
- Всички съобщения се състоят от азбука. Например тази статия е съобщение. Тогава той се състои от символите на руската азбука.
- Под символа можем да разберем минималната значима частица от азбуката. Също така неделими частици се наричат атоми. Символите в руската азбука са "а", след това "б", "в" и т.н.
- На теория азбуката не трябва да се кодира по никакъв начин. Например, в печатна книга символите на азбуката означават, че те нямат кодиране.

Но на практика ние имаме следното: компютърът не разбира какво са буквите. Следователно, за да предаде информационно съобщение, то трябва първо да бъде кодирано на език, разбираем за компютъра. За да продължим напред, е необходимо да въведем допълнителни условия.
Каква е силата на азбуката
Под мощност на азбуката имаме предвид общия брой символи в него. За да разберете каква е силата на азбуката, просто трябва да преброите броя на знаците в нея. Нека го разберем. За руската азбука силата на азбуката е 33 или 32 символа, ако не използвате "e".
Да предположим, че всички символи в нашата азбука се срещат с еднаква вероятност. Това предположение може да се разбере по следния начин: да предположим, че имаме торба с подписани кубчета. Броят на кубчетата в него е безкраен и всеки е подписан само с един символ. След това, с равномерно разпределение, без значение колко кубчета излизаме от чантата, броят на кубчетата с различни символи ще бъде един и същ, или ще се стреми към това с увеличаване на броя на кубовете, които изваждаме от чантата.
Оценка на теглото на информационните съобщения
Преди почти сто години американският инженер Ралф Хартли извлече формула, с която можете да оцените количество информация в съобщението. Формулата му работи за еднакво вероятни събития и изглежда така:
i = log 2 M
Където "i" е броят на неделимите информационни атоми (битове) в съобщението, "М" е силата на азбуката. Ние следваме. С помощта на математически преобразувания можем да определим, че мощността на азбуката може да се изчисли по следния начин:
М = 2 i
Тази формула в обща форма задава връзката между броя на еднакво вероятните събития "М" и количеството информация "i".
Изчислете силата
Вероятно вече знаете от курса по компютърни науки, че в съвременните компютърни системи, изградени върху архитектурата на фон Нойман, се използва бинарна система за кодиране на информация. И двете програми и данни са кодирани по този начин.
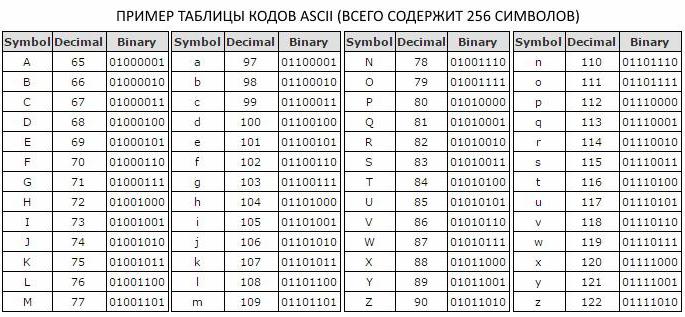
За да представи текста в изчислителната система, използвайте единен код от осем бита. Кодът се счита за унифициран, защото съдържа фиксиран набор от елементи - 0 и 1. Стойностите в такъв код се определят от определен ред на тези елементи. С помощта на осем-битов код можем да кодираме съобщения с тегло 256 бита, защото по формулата Хартли: M 8 = 2 8 = 256 бита информация.
Тази ситуация с кодирането на символи в двоичен код се е развила исторически. Но теоретично можем да използваме други азбуки, за да представим данните. Така например, в четирибуквената азбука, всеки знак ще има тегло не от един, а от два бита, в осемзначна азбука - 3 бита и така нататък. Това се изчислява с помощта на двоичния логаритъм, даден по-горе ( i = log 2 M ).
Тъй като в азбуката с капацитет 256 бита, се разпределят осем двоични цифри за един символ, беше решено да се въведе допълнителна мярка от информация - байтове. Един байт съдържа един символ от ASCII кодовата таблица и съдържа осем бита.
Как да измерим информацията
в прописном и строчном варианте, цифры, символы знаков препинания и другие базовые символы. Осем-битовото кодиране на текстови съобщения, което се използва в ASCII кодовата таблица, ви позволява да поставите основния набор от латински и кирилица в главни и малки букви, цифри, препинателни знаци и други основни символи.
За да се измери по-голямо количество данни, използвайте специални префикси за думите байт и бит. Такива прикачени файлове са показани в таблицата по-долу:
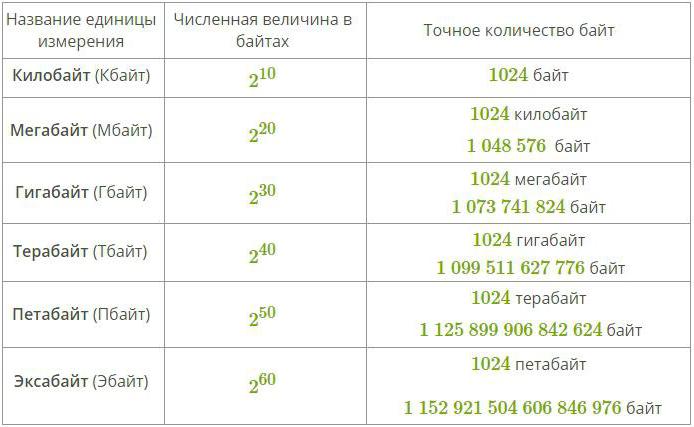
Много хора, които са изучавали физика, ще твърдят, че би било рационално да се използват класически представки за обозначаване на единици информация (като кило и мега), но в действителност това не е напълно правилно, защото такива префикси към стойности означават умножение с една или друга степен от десет. когато бинарната система от измервания се използва навсякъде в компютърните науки.
Поправя имената на блоковете с данни
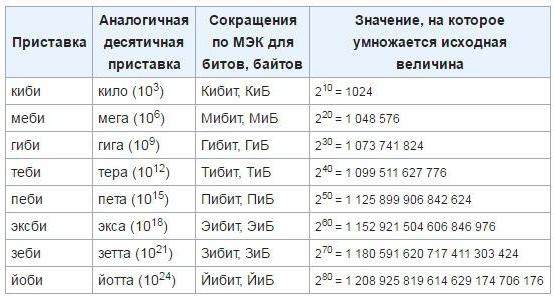
За да се премахнат неточностите и неудобствата, през март 1999 г. Международната комисия по електротехника одобри нови единици към блоковете, които се използват за определяне на количеството информация в електронните компютърни технологии. Такива представки са "mebi", "kibi", "gibi", "tebi", "eksbi", "petit". Досега тези единици все още не са вкоренени, така че най-вероятно е необходимо време за въвеждането на този стандарт и началото на широкото му използване. Как да направим прехода от класическите единици към ново одобрените, можете да определите следната таблица:
Да предположим, че имаме текст, съдържащ K символа. След това, използвайки азбучния подход, можете да изчислите количеството информация V, което съдържа. Тя ще бъде равна на произведението на силата на азбуката от информационното тегло на един символ в него.
Чрез формулата Хартли знаем как да изчислим количеството информация чрез двоичния логаритъм. Ако приемем, че броят на буквите на азбуката е равен на N и броят на символите в записа на информационното съобщение е равен на K, получаваме следната формула за изчисляване на информационния обем на съобщението:
V = K 2 log 2 N
Азбучният подход показва, че обемът на информацията ще зависи само от силата на азбуката и размера на съобщенията (т.е. броя на символите в нея), но по никакъв начин няма да бъде свързан със семантичното съдържание за дадено лице.
Примери за изчисляване на мощността
В класната стая компютърната наука често дава задачата да намери силата на азбуката, дължината на съобщението или обема на информацията. Ето една от следните задачи:
"Текстов файл заема 11 KB дисково пространство и съдържа 11264 символа. Определете силата на азбуката на този текстов файл."
Какво ще бъде решението, което можете да видите на картинката по-долу.

Така азбуката с капацитет от 256 символа носи само 8 бита информация, която в компютърната наука се нарича един байт. Байт описва 1 символ от ASCII таблицата, който, ако мислите за него, изобщо не е много.
Има един байт или малко?
Съвременните хранилища на данни като центровете за данни на Google и Facebook съдържат не по-малко от десетки петабайта информация. Точното количество данни, обаче, ще бъде трудно да се изчисли дори сами по себе си, защото тогава ще трябва да спрете всички процеси на сървърите и близките потребители на достъп до записване и редактиране на тяхната лична информация.

Но за да си представим такива немислими количества данни, е необходимо ясно да се разбере, че всичко е съставено от малки детайли. Необходимо е да се разбере каква е силата на азбуката (256) и колко бита съдържат 1 байт информация (както си спомняте, 8).