Какъв е моментът на инерцията: формули за пръта и колелото

Всяко движение на тела в пространството, чиято траектория е кръг, предполага да се знае не само ъгловата скорост, но и моментът на инерцията за описанието на това движение. Какъв е моментът на инерцията, както и това, което е за пръта и колелото, тази статия ще отговори.

Въртене и момент на инерция

Физическото количество, което се нарича момент на инерцията, се обозначава по правило с буквата I и се появява във физиката, когато се разглежда ъгловия момент на материална точка, която се върти около една ос. Ъгловият момент L в скаларна форма се записва със следния израз:

L = r * m * v

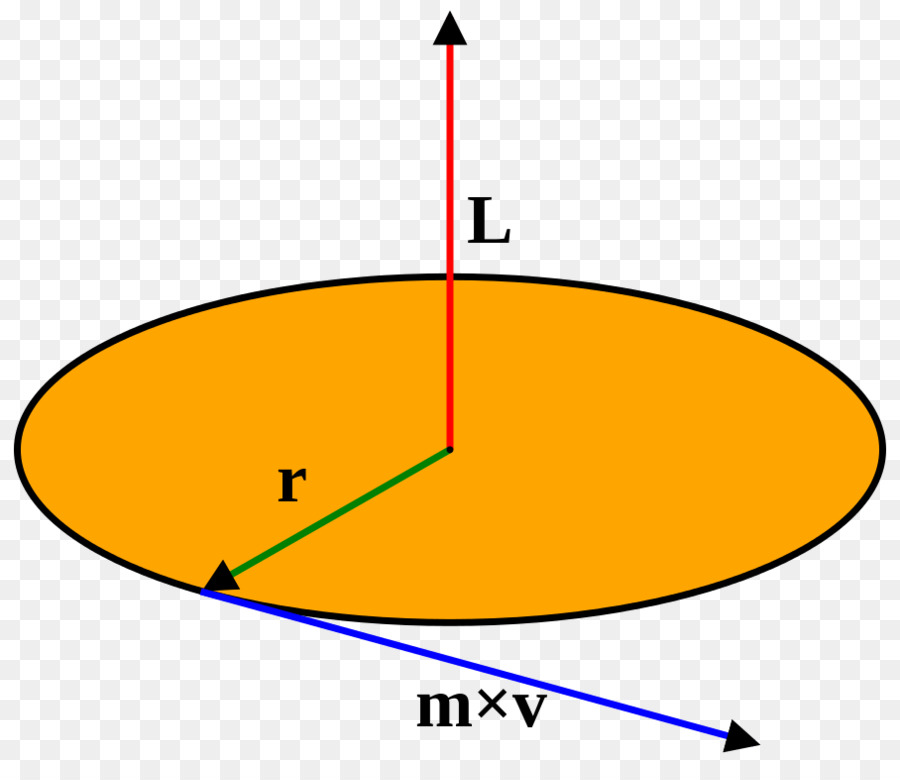
Тук r е разстоянието до оста на материалната точка, m е неговата маса, v е линейната скорост. Използвайки връзката на последното с ъгловия σ, получаваме израза:

L = r ² * m * ω, където ω = v / r

Отговаряйки на въпроса какъв е моментът на инерцията, трябва да се каже, че това е стойността I = r ² * m. Тоест, тя зависи от масата на въртящия се обект, тя нараства бързо с увеличаване на разстоянието до оста и се измерва в kg * m ² .

Общ израз за момента на инерцията

Формулата, въведена в предишния параграф за стойността на I, е валидна, ако размерите на обекта са незначителни в сравнение с разстоянието до оста r (Земята се върти около нашата звезда). Ако линейните размери на обекта станат съпоставими с разстоянието r, тогава е необходимо да се изчисли I, за да се използва по-обща формула, която е дадена по-долу:

I = ( _m (r ² * dm)

Това показва, че интегренът е моментът на инерцията на материалната точка. Сумата от всички моменти от точки с маса dm е общият момент на инерцията I за цялото тяло.

Тази формула е мощен инструмент за определяне на I тялото на абсолютно всякаква форма. Съгласно формулата стойността на I е адитивна, т.е. тя ви позволява да разделяте тялото на отделни части, да изчислявате техните инерционни моменти и след това да добавите резултатите, за да получите стойността на тялото I.

Физическият смисъл на I

Знаейки какъв е моментът на инерцията, е необходимо да кажем няколко думи за това как нейната стойност влияе на поведението и характеристиките на ротация на реални обекти.

Голяма стойност на I води до факта, че тялото е много трудно да се върти около оста. За да направите това, трябва да извършите значителна работа и да положите значителни усилия. Пример за тяло с голям I е автомобилен маховик - тежък метален диск, твърдо монтиран на коляновия вал на двигателя. Напротив, ако стойността на системата I е малка, тогава тя може бързо да бъде разгъната и също толкова бързо и лесно да бъде спряна. Пример за това е алуминиевата джанта на колело за велосипеди.

Горепосочената дискусия предполага, че моментът на инерцията се характеризира с инерцията на ротационния процес, т.е. изпълнява същата роля като масата на тялото, когато към нея се прилага сила, за да придаде ускорение.

Разликата между масата и момента на инерцията лежи не само в мерните единици, но и във факта, че последната е функция на ротационната система, а не само геометрията на тялото и неговата маса.

Моментът на инерция около оста на въртене, пресичаща центъра на масата на пръта

Разгледайте пример за използване на интегрална формула за решаване на реални проблеми. На първо място, решаваме един прост проблем: има тънък прът с дължина l и маса m. Оста се върти перпендикулярно на този прът през центъра на масата на обекта. Необходимо е да се определи стойността на I за тази система.

Пишем общата формула за инерцията на момента на пръчката около оста, имаме:

I = ( _m (r ² * dm)

Тъй като остата е перпендикулярна на въпросното тяло, а самият прът е с безкрайно малка дебелина, възможно е да се пресече на тънки слоеве с равнини, успоредни на оста. В този случай откриваме, че елемент от маса dm може да бъде представен със следното уравнение:

dm = ρ * s * dr

Тук ρ е плътността на материала, S е напречното сечение, което е постоянно и се стреми към нула (прътът е безкрайно тънък). Заменете този израз в общата формула:

I = ρ * S * ∫ ^{+ l / 2} _{-l / 2} (r ² * dr)

Отбележете, че заместените интегрални граници за r съответстват на състоянието на проблема (оста делят пръчката на две равни части). Извършвайки интеграция, получаваме:

I = ρ * S * (r 3/3) | ^{+ l / 2} _{-l / 2} = m * l 2/12, където m = ρ * S * l

Така инерционният момент на тънък прът, когато оста минава през центъра на масата, е 12 пъти по-малък от този за материална точка от същата маса, разположена на разстояние l от оста.

Стойността на I за пръчката с оста на въртене в края на обекта

Помислете какъв е моментът на инерцията в малко по-различна ситуация. Ние имаме един и същ обект (тънък прът), но сега оста минава през края. Как ще се промени моментът на инерцията в този случай? Използвайки същия метод за разделяне на пръчка и последваща интеграция, както в предишния параграф, получаваме:

I = ρ * S * ∫ ^l ₀ (r ² * dr)

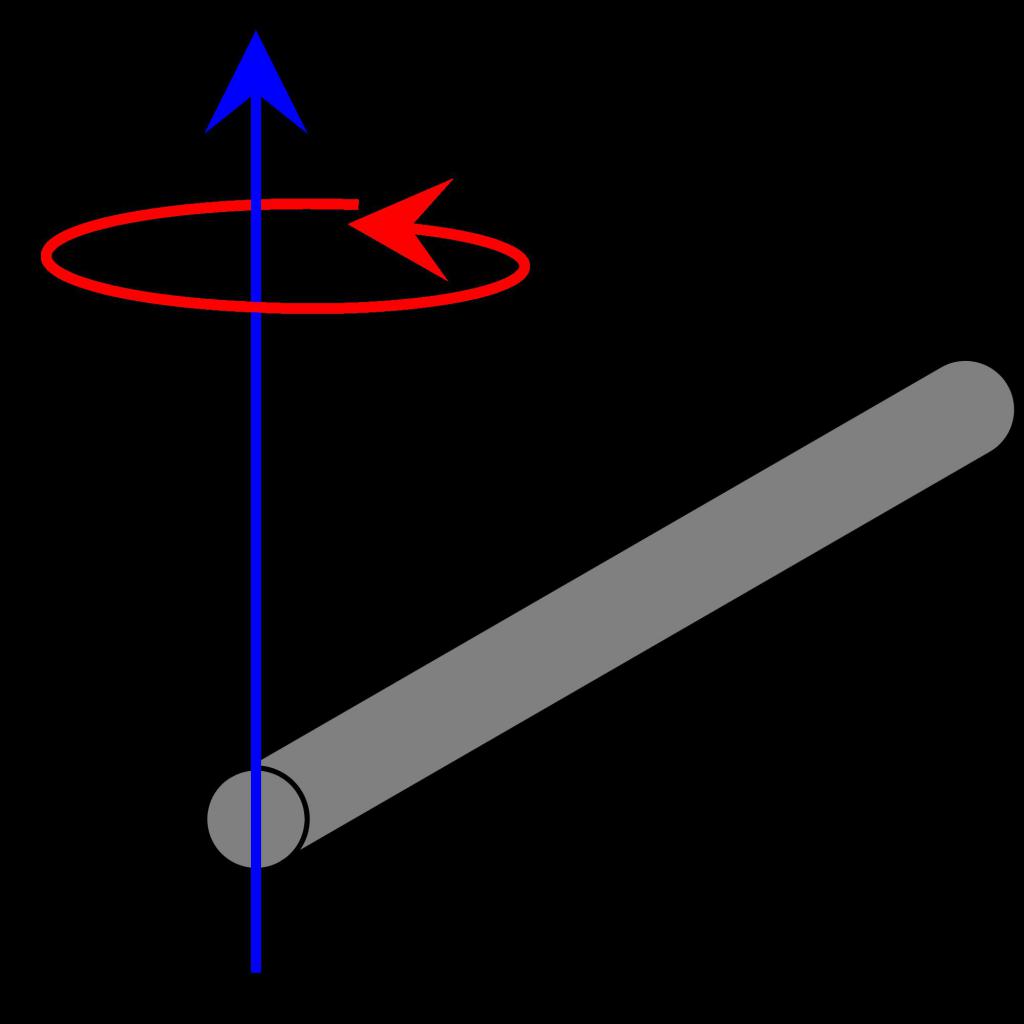
Имайте предвид, че само границите на интеграция са се променили. Решението е следното равенство:

I = m * l 2/3

Изразът показва, че същият прът ще има 4 пъти по-голям инерционен момент (по-труден за завъртане), ако оста на въртене се премества от центъра към ръба.

Като се има предвид решението на тези два проблема, трябва да се направи важен извод: при изчисляване на стойността на I е невъзможно да се намали цялата маса на обекта до неговия център и да се извърши изчислението както за материална точка. Изчислението трябва да се извърши само с помощта на интегрален израз.

Стойност за колелото

Моментът на инерция на колелото може да се определи, като се използва свойството на добавката на разглежданото количество. За да направите това, умствено разглобете колелото в отделни части, които представляват спиците и джантата. Тъй като иглата е тънка пръчка, а оста й на въртене минава през края, формулата, получена в предишния параграф, е валидна за нея.

Що се отнася до джантата, неговият момент на инерция е подобен на този за материална точка, разположена на разстояние от радиуса на колелото и имаща маса на джантата.

Добавяйки моментите на инерция на всички елементи, получаваме:

I = n * m _c * r 2/3 + m _o * r ²

Тук m _c и m _o са спиците и съответно масите на джантата, n е броят на спиците. Ако всички спици тежат много по-малко от ръба, то инерцията на колелата ще бъде равна на:

I = m _o * r ^2, ако n * m _c < о

Познаването на стойността на I за колелото е важно при изчисляване на ъгловата скорост и ъгловия момент на въртене на колелата на всяко превозно средство (кола, велосипед).