Какво е конус? Концепция и снимка

Стереометрията е важен раздел от геометрията, предмет на изследване на който са свойствата и характеристиките на фигурите в триизмерното пространство. В тази статия ще разгледаме една от такива обемни фигури. Нека се запознаем с въпроса какво е конус.

Конусна цифра

Даваме най-общо определение за конус. Под тази фигура разбираме повърхността, която се формира в резултат на свързването на правите сегменти на определена точка в пространството с всички точки на дадена крива. В този случай, указаната точка в пространството не трябва да бъде в равнината на кривата. Например, ако кривата има формата на парабола, фигурата, получена по описания метод, ще се нарича параболичен конус, ако кривата е елипса, конусът ще бъде елиптичен и така нататък.

След като дадем геометрична дефиниция на това какво представлява конусът, представяме снимка, която показва визуално възможни форми на тази фигура.

Разглеждайки тази снимка, много хора видяха в нея формата на детска шапка, която носеше Буратино, вафлена чаша от сладолед под формата на рог или предупредителен оранжев и черен конус.

Конус на геометрични елементи

За да разберем по-добре въпроса какво представлява конусът, трябва да цитираме геометричните имена на елементите на тази пространствена фигура.

Конусът е ограничен от две повърхности. Първата се нарича база. Това е равнина, която е ограничена от кривата, отбелязана по-горе. Например, тя може да бъде кръг или елипса. Втората повърхност е страна за формата и се нарича конична. Тя не лежи в същата равнина, а може да се превърне в плоска фигура, както ще бъде разгледано по-долу.

Един от важните елементи на конуса е неговият връх. Тази точка ограничава коничната повърхност. Към него са свързани всички точки на основната крива.

Сегментът, който свързва горната част на основата, нарича се образуващата, или образува конус. На свой ред, кривата, ограничаваща основата, се наричаше директна, или водещата фигура.

Площите на коничната повърхност и основата се прибавят към общата площ на конуса. Обемът на пространството, който ограничава тези две повърхности, е обемът на конуса.

Кръгъл прав конус и неговите линейни характеристики

По-горе беше дадено общо определение за това кой конус. Въпреки това, често на практика и в геометричните проблеми има специфична форма на тази фигура - прав кръгъл конус. Това е показано по-долу.

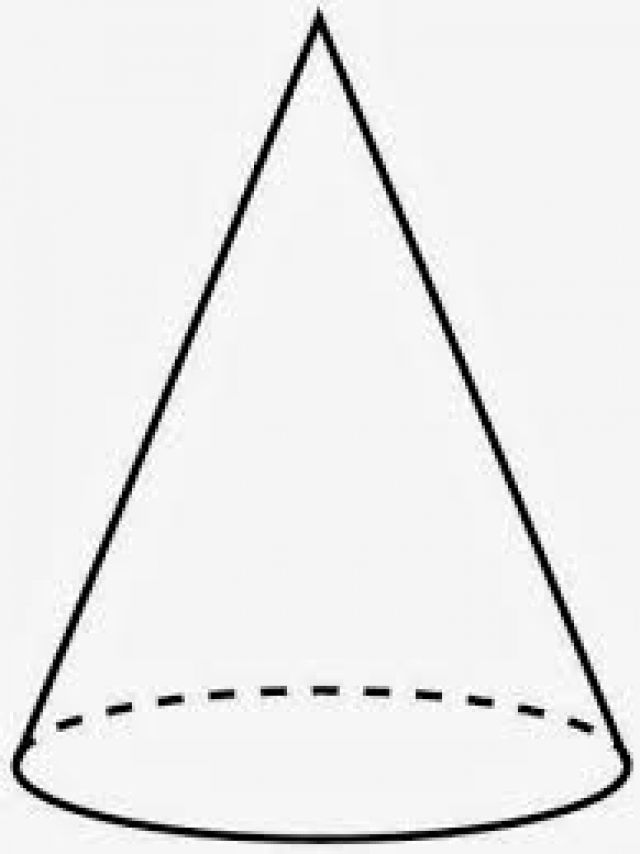
В основата на тази цифра е кръг. Тя се нарича права, защото перпендикулярът, падащ от основата му от височина, ще пресича кръга в неговия точен център. Ако това условие не беше изпълнено, тогава можем да говорим за наклонен конус.

Линията, която свързва върха с центъра на кръга, се нарича оста на фигурата. Също така е и оста на въртене на конуса. Всъщност, ако вземете правоъгълен триъгълник и започнете да го завъртите около един от краката, тогава получената фигура ще бъде прав конус с кръгла основа. Този метод за получаване на конус е показан схематично по-долу.

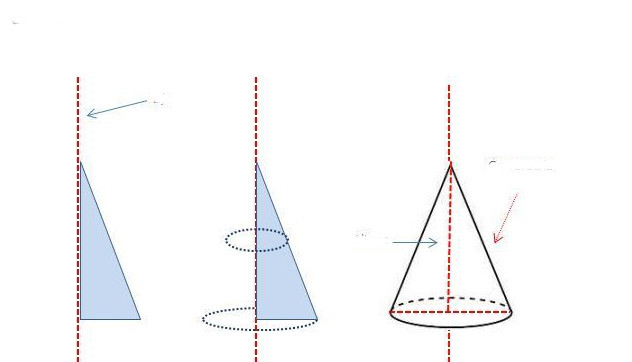
Може да се види, че генераторът ще бъде равен на дължината на хипотенузата на триъгълника. Кракът, около който е извършено въртенето, ще стане височина на триизмерната фигура, а вторият крак ще бъде равен на радиуса на конуса (радиуса на кръговата основа).

Една от важните черти на въпросната фигура е, че дължините на всички генератори за нея са еднакви. Този факт ни позволява, като използваме Питагоровата теорема, да напишем математическата връзка между трите основни линейни параметри на формата:

g ² = r ² + h ²

Квадратът на генератора на прав кръгъл конус g е равен на сумата от квадратите на неговия радиус r и височината h.

След като разгледаме въпроса какво представлява конус с права линия с кръгла основа, нека покажем как е възможна неговата повърхност и обем.

Определяне на повърхността

Както вече беше отбелязано, повърхността на фигурата е оформена от конична повърхност и плоска основа. Каква е тяхната площ? С увереност можете да отговорите на този въпрос, ако погледнете плоско сканиране на кръгъл конус. Изрязваме основата от страничната повърхност и го разрязваме по образуващата, получаваме следния резултат.

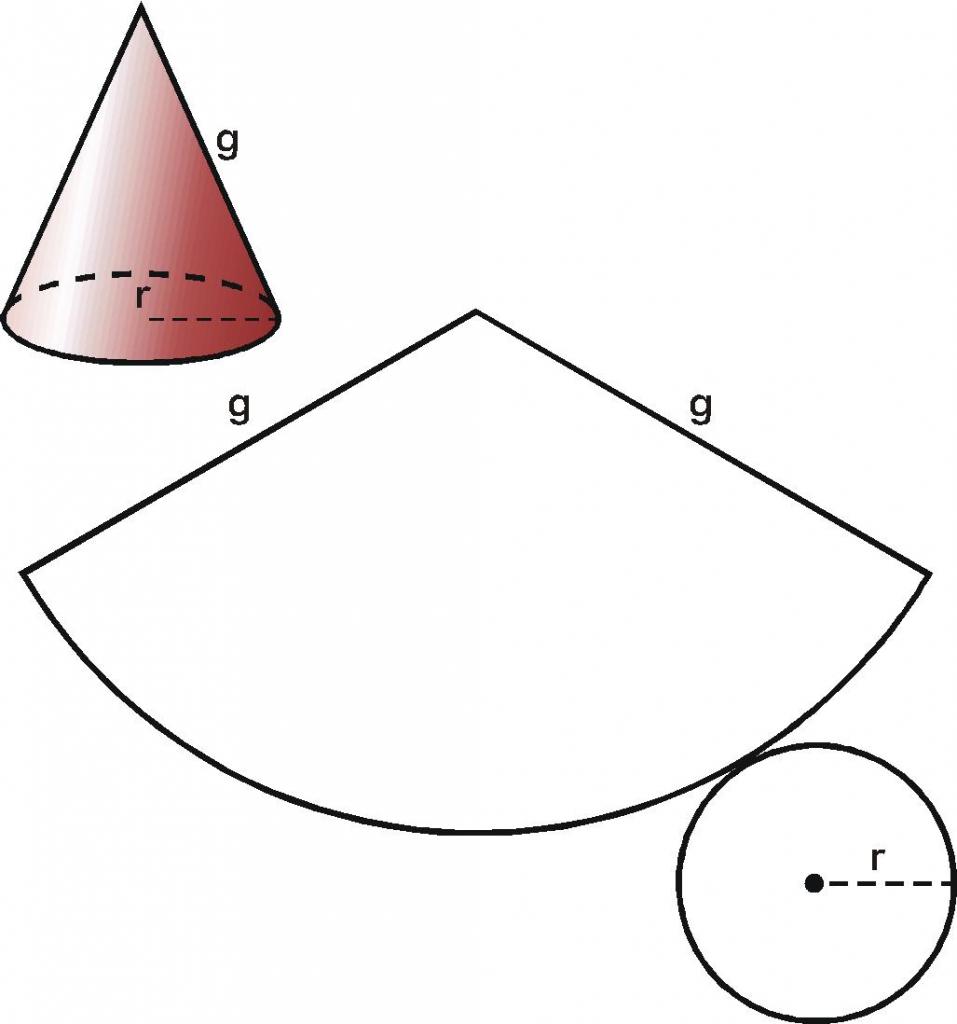
Няма проблеми с определянето на площта на окръжността. Формулата за неговата област е позната на всеки ученик. Запишете го:

S _o = pi * r ²

Символът S _o е площта на основата на фигурата.

Страничната повърхност на конуса върху плоско сканиране е представена от кръгъл сектор, радиусът на който е равен на дължината на генератора, а дължината на дъгата, върху която секторът лежи, е равна на дължината на обиколката на основата. Тези данни ни позволяват да определим еднозначно областта на сектора. Няма да даваме междинни изчисления за получаване на формула за квадрата S _{b на} страничната повърхност на конуса. Пишем крайния резултат:

Sb = pi * g * r

Тъй като генераторът g е винаги по-голям от радиуса r, площта на страничната повърхност на фигурата ще надвиши, за всички параметри, тази на основата.

Формулата за общата площ приема формата:

S = S _o + S _b = pi * r * (r + g)

Определяне на обема на фигурата

Читателите може да са забелязали, че формата на конуса наподобява нещо като пирамида, само че неговата странична повърхност е гладка и не е оребрена, като пирамида. Тази аналогия има геометрично оправдание, тъй като увеличаването на броя на страничните повърхности на пирамидата до безкрайност го превръща в конус. Този факт позволява да се запише за обема на конуса точно същата формула както за обема на пирамидата. Имаме:

V = 1/3 * h * S _o

Забележете, че няма значение коя затворена крива образува основата на конуса, също така няма значение дали фигурата е права или наклонена, формулата ще бъде валидна във всички тези случаи.

За конус на кръг, изразът за V приема специфична форма:

V = 1/3 * pi * r ^{2 *} h

Задачата да се определи площта на конуса през нейния обем

Ние показваме как да използваме написаните формули.

Да предположим, че обемът на кръгъл конус е 50 cm ³ . Необходимо е да се изчисли неговата повърхност, ако радиусът r е три пъти по-малък от височината h.

Пишем формулата за обема и връзката на височината h с радиус r в съответствие със състоянието на проблема:

V = 1/3 * pi * r ^{2 *} h;

h = 3 * r.

От тези уравнения получаваме:

V = 1/3 * pi * r ² * 3 * r =>

r = (V / pi) ≈ 2.516 cm;

h = 3 * ∛ (V / pi) ≈ 7.547 cm.

Получените стойности ни позволяват да изчислим дължината на генералния конусен генератор g:

g = √ (h2 + r2) = 7.955 cm.

Формулата за площта на фигурата е:

S = pi * r * (r + g)

Определихме всички необходими количества (r и g). Подставяйки техните числови стойности в равенство, получаваме отговор: S = 82.72 cm ² .