Теоремата на Виета: примери за нейното използване при работа с квадратични уравнения
Когато изучават методи за решаване на уравнения от втори ред в училищен курс по алгебра, вземете под внимание свойствата на получените корени. Понастоящем те са известни като Виетската теорема. Примери за използването му са дадени в тази статия.
Квадратично уравнение
Уравнението от втори ред е уравнение, което е показано на снимката по-долу.
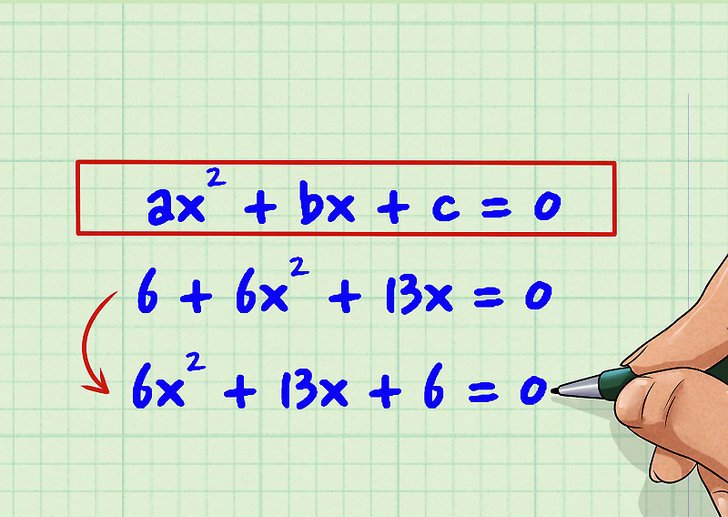
Тук символите a, b, c са някои числа, които се наричат коефициенти на въпросното уравнение. За да се реши равенството, е необходимо да се намерят стойностите на x, които правят това вярно.
Отбележете, че тъй като максималната стойност на степента, в която X се повишава, е равна на две, тогава броят на корените в общия случай също е равен на два.
Има няколко начина за решаване на този вид равенство. В тази статия ще разгледаме една от тях, която включва използването на така наречената Viet теорема.
Формулиране на Виетската теорема

В края на XVI в. Известният математик Франсоа Вите (французин) отбелязва, анализирайки свойствата на корените на различни квадратични уравнения, че някои комбинации от тях удовлетворяват определени отношения. По-специално, тези комбинации са техният продукт и сума.
Теоремата Виета установява следното: корените на квадратичното уравнение с тяхната сума дават съотношението на линейните към квадратичните коефициенти, взети с противоположния знак, и когато се произвеждат, те водят до съотношението на свободния член към квадратичния коефициент.
Ако общата форма на уравнението е написана така, както е представена на снимката в предишния раздел на статията, то математически тази теорема може да бъде написана под формата на две равенства:
- r2 + r1 = -b / a;
- r 1 x r 2 = c / a.
Когато r 1 , r 2 е стойността на корените на въпросното уравнение.
Тези две уравнения могат да се използват за решаване на много различни математически проблеми. Използването на Виетската теорема в примерите с решението е дадено в следващите раздели на статията.
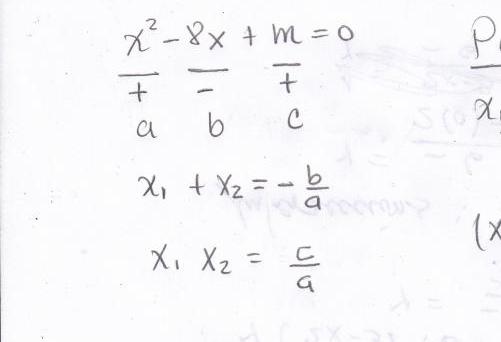
Проблем номер 1: възстановяване на уравнението
Представяме следния проблем за използването на Виетската теорема. Пример за уравнението е даден по следния начин: -3.4 * x - 3 * s * x 2 + k = 0. Трябва да намерите стойностите на s и k, като знаем, че две числа са решенията на това уравнение: -1,2 и 4.
Първо трябва да определите стойността на коефициентите в този израз. От това следва, че a = -3 * s, b = -3.4 и c = k.
Сега можете да използвате теоремата на Виет. За сумата от корените получаваме следното равенство: -1.2 + 4 = - (- 3.4) / (-3 * s), откъдето получаваме, че s = -0.40476 (препоръчва се да се използва калкулатор, за да се изчисли този израз). Това означава, че a = -3 * s = 1.21429. За да произвеждаме корени, имаме:
(-1,2) * 4 = k / 1,21429, откъдето k = -5,82859.
Реконструираното уравнение ще съответства на формата: -3.4 * x + 1.21429 * x 2 - 5.82859 = 0. За да се провери дали проблемът е решен правилно и ако има грешка при решаването му, е необходимо да се заменят известните коренови стойности в възстановения израз. Получаваме: -3.4 * (-1.2) + 1.21429 * (-1.2) 2 - 5.82859 = 0.00001 ≈ 0 и -3.4 * (4) + 1.21429 * ( 4) 2 - 5.82859 = 0.00005 ≈ 0.
Както виждаме, получените равенства наистина са удовлетворени. Малка грешка се дължи на факта, че при възстановяване на уравнението, закръгляваме получените числа до 5 знака след десетичната запетая.
Задача номер 2: намерете корените на уравнението
Решението на квадратичните уравнения по Виетската теорема (виж пример по-долу) е възможно не във всички случаи. Това означава, че този метод не е универсален, защото ако коефициентите на уравнението се окажат "неудобни", тогава няма да работи.
Универсалните методи за решаване на този тип изразяване са използването на дискриминант или допълнение към пълен квадрат. Въпреки това, важността на теоремата на Виет в този случай се крие във факта, че тя позволява да се отгатне за неизвестни корени, без да се извършват сложни математически изчисления.
Например, следният израз е даден: -x 2 + 2 * x + 3 = 0. Трябва да използваме теоремата Vieta, за да намерим решения на това равенство. Нека корените му са числата r 1 и r 2 . След това можете да напишете следната система от уравнения:
r1 + r2 = -2 / (-1) = 2;
r1 * r2 = 3 / (-1) = -3.
Сега е необходимо да се познае коя сума от числата е две, а техният продукт ще бъде -3. Очевидно това са числата 3 и -1. Те ще бъдат корените на уравнението.
Ако вникнем малко в темата, трябва да отбележим, че всяко уравнение от втори ред, което лесно се представя като продукт на два фактора, може да бъде решено с помощта на дискутираната теорема. Всъщност в този случай можем да напишем (3-x) * (x + 1), ако разширим скобите, получаваме оригиналния израз.
Проблем номер 3: сумата на квадратите
Даваме друг пример за Виетската теорема с решение. Като се има предвид уравнението:
6 * x 2 - 13 * x + 11 = 0. Необходимо е да се намери сумата от квадратите на двата й корена, т.е. (r 1 ) 2 + (r 2 ) 2 .
Разбира се, първо можете да разрешите това уравнение по един от начините и да отговорите на въпроса за проблема. Обаче, ако си припомним Виетската теорема и свойството на квадрата сума, тогава няма нужда от това.
Трябва да се помни как се изчислява сумата от две числа на квадрат. Тогава откриваме, че за да се намери неизвестната сума от квадрати, е необходимо да се изчисли стойността на израза (r 1 + r 2 ) 2 - 2 * r 1 * r 2 . Използваме и двете равенства на разглежданата теорема, получаваме: (13/6) 2 - 2 * 11/6 = 1.02 (7) (7 в периода).
Така, чрез прилагане на Виетската теорема, спестихме време за решаване на уравнението. Като цяло, свойствата на корените могат да се използват за всякакви задачи, които включват изчисляването на различните им комбинации.