Равномерно движение. Формула за равномерно движение.

Запознаването с класическия курс на физиката започва с най-простите закони, които се подчиняват на движението на тела в пространството. Праволинейното равномерно движение е най-простият вид промяна в положението на тялото в пространството. Такова движение се изучава в кинематичната част.

Противник на Аристотел

Галилео Галилей остава в историята на историята като един от най-големите природолюбители от късния Ренесанс. Той се осмелил да провери твърденията на Аристотел - нечувано ерес в онези времена, защото учението на този древен мъдрец беше силно подкрепено от църквата. Идеята за равномерно движение не се разглеждаше тогава - тялото или се движеше „общо“, или се намираше в покой. Необходими са многобройни експерименти, за да се обясни естеството на движението.

Галилееви експерименти

Класически пример за изучаване на движението е известният експеримент на Галилео, когато той хвърля различни тежести на известния Наклонената кула в Пиза. В резултат на този експеримент стана ясно, че телата с различни маси падат с една и съща скорост. По-късно експериментът продължава в хоризонтална равнина. Галилео предположи, че при липса на триене всяка топка ще се търкаля по слайда за произволно дълго време, а скоростта му също ще бъде постоянна. Така, експериментално, Галилео Галилей откри същността на първия закон на Нютон - при отсъствието на външни сили, тялото се движи по права линия с постоянна скорост. Праволинейното равномерно движение е изразът Първият закон на Нютон. В момента различни видове движение участват в специални физика - кинематика. Преведено от гръцки, това име означава доктрината за движение.

Нова координатна система

Анализът на равномерното движение би бил невъзможен без създаването на нов принцип за определяне на положението на телата в пространството. Сега го наричаме праволинейна координатна система. Неговият автор е известният философ и математик Рене Декарт, благодарение на който наричаме координатна система картезианска. В тази форма е много удобно да се представи траекторията на тялото триизмерно пространство и анализира това движение, обвързвайки позицията на тялото с координатните оси. Правоъгълната координатна система се състои от две права пресичащи се под прав ъгъл. Точката на пресичане обикновено се приема като начало на измерванията. Хоризонталната линия се нарича абсциса, вертикалната линия е ординатата. Тъй като живеем в триизмерно пространство, към равнинната координатна система се добавя трета ос - тя се нарича апликат.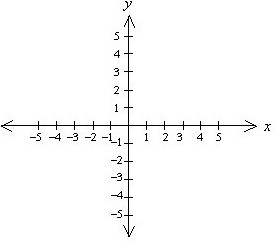

Определяне на скоростта

Скоростта не може да бъде измерена, докато измерваме разстоянието и времето. Това винаги е стойността на деривата, който е записан като съотношение. В най-общата форма скоростта на тялото е равна на съотношението на изминатото разстояние до изминалото време. Формулата за скорост е: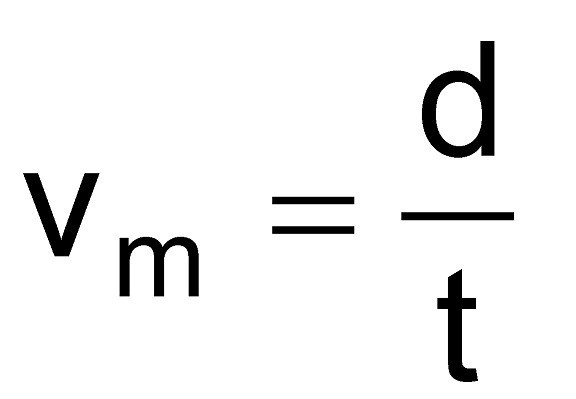

Където d е изминатото разстояние, t е изминалото време.

Посоката пряко влияе върху векторното обозначение на скоростта (количеството, което определя времето е скаларно, т.е. няма посока).

Разбиране на равномерното движение

При равномерно движение тялото се движи по права линия с постоянна скорост. Тъй като скоростта е векторна величина, нейните свойства се описват не само по брой, но и по посока. Затова е по-добре да се изясни определението и да се каже, че скоростта на равномерното праволинейно движение е постоянна по величина и посока. За да се опише праволинейното равномерно движение, достатъчно е да се използва декартова координатна система. В този случай оста OX ще бъде удобно поставена в посоката на движение.

При равномерно изместване, положението на тялото във всеки период от време се определя само от една координата, х. Посоката на движение на тялото и вектора на скоростта са насочени по оста х, като началото на движението може да бъде отчетено от нулевата марка. Следователно, анализът на движението на тялото в пространството може да се сведе до проекция на траекторията на движение по оста OX и да опише процеса на алгебричните уравнения.

Равномерно движение по отношение на алгебра

Да предположим, че в даден момент във времето t ₁ тялото е в точка на оста х, чиято координата е x ₁ . На свой ред тялото ще промени мястото си за известно време. Сега координатата на местоположението му в пространството ще бъде x ₂ . Чрез намаляване на разглеждане на движението на тялото до неговото местоположение по координатната ос, може да се определи, че пътят, по който изминатото тяло е равно на разликата между началната и крайната координати. Алгебрично, това се пише като: Δs = x ₂ - x _1.

Размер на преместването

Стойността, която определя движението на тялото, може да бъде повече и по-малка от 0. Всичко зависи от начина, по който тялото се движи спрямо посоката на оста. Във физиката могат да бъдат записани както отрицателни, така и положителни измествания - всичко зависи от избраната за справка координатна система. Праволинейното равномерно движение се осъществява със скорост, която се описва с формулата: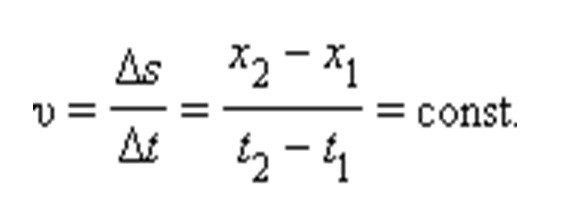

В този случай скоростта ще бъде по-голяма от нула, ако тялото се движи по оста OX от нула; по-малко от нула - ако движението се движи от дясно на ляво по оста х.

Такъв кратък запис отразява същността на равномерното праволинейно движение - каквото и да се променя координатите, скоростта на движение остава непроменена.

Галилео, ние дължим друга брилянтна идея. Анализирайки движението на тялото в свят, лишен от триене, ученият настоя, че силите и скоростите не зависят един от друг. Това блестящо предположение беше отразено във всички съществуващи закони на движението. По този начин силите, действащи върху тялото, са независими един от друг и действат така, сякаш другите не съществуват. Прилагайки това правило към анализа на движението на тялото, Галилео разбира, че цялата механика на един процес може да се разложи на сили, които са геометрично (векторно) или линейни, ако действат в една посока. Приблизително ще изглежда така:

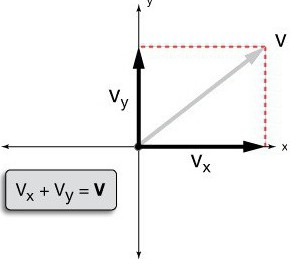
Какво означава единното движение тук? Много е просто. При много малки пропуски по пътя скоростта на тялото може да се разглежда като еднородна, права линия. По този начин имаше брилянтна възможност да изучаваме по-сложни движения, като ги свеждахме до прости. Така се изследва равномерното движение на тялото по кръг.

Равномерно движение по окръжност

Единни и равномерно ускорено движение може да се наблюдава при движението на планетите в орбитите им. В този случай, планетата участва в два типа независими движения: тя се движи равномерно по периферията и същевременно се движи със същата скорост към Слънцето. Такова сложно движение се обяснява със силите, действащи върху планетите. Диаграмата на въздействието на планетарните сили е показана на фигурата: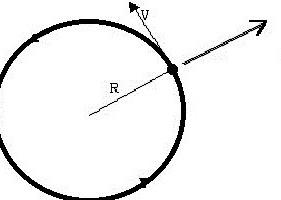

Както виждате, планетата участва в две различни движения. Геометричното добавяне на скорости ще ни даде скоростта на планетата на даден сегмент от пътя.

Равномерното движение е основа за по-нататъшно изучаване на кинематиката и физиката като цяло. Това е елементарен процес, към който могат да се намалят много по-сложни движения. Но във физиката, както и навсякъде другаде, великото започва с малки неща и изстрелването на космически кораб в безвъздушно пространство, опериращо с подводници, не трябва да забравяме и онези прости експерименти, на които Галилео веднъж е тествал откритията си.