Дървото на решенията е пример. Методи за вземане на решения

В повечето случаи, вземането на решения може да се извърши със светкавична скорост, въз основа на нашия опит, както се казва, на око. Но понякога тази опция не се счита за адекватна. И какво да правя в този случай? Особено за тези умни хора са разработени методи за вземане на решения. Те позволяват постепенно и с минимални отклонения да се изработи алгоритъмът на действията.

Обща информация

А най-интересният момент за нас е методът на дървото на решенията. Какъв е той? Къде се използва? Методът на Дърво на решенията е графично описание на определени действия и състояния на околната среда, които показват съответните вероятности и печалби за определени комбинации. Използва се за оценка на рисковете от проекти, когато е необходимо да се инвестират средства за значителен период от време. Причината за използването му е да има две или повече последователни решения. И те трябва да текат от предишните и / или групи от състояния на околната среда.

Относно формалната структура

Какви елементи се използват за създаване? Това е:

1. Възел за решение. Използва се за характеризиране на момента на избор.
2. Линия, представляваща алтернативата.
3. Възел за събитие Използва се за означаване на определена случайност, която се случва.
4. Ред, описващ средата, която е резултат от непредвидено събитие.
5. Резултатен възел. Използва се за обозначаване на общите стойности. Тя е свързана със специфично състояние на околната среда и решения.
6. Възел за означаване на междинен резултат. Необходимо е да се посочи ситуация, в която следва да се вземе друго решение.

строителство

Как се използва методът на дървото на решенията на практика? За да се формулират различни сценарии за развитие, е необходимо да има цялата необходима и надеждна информация, която отчита вероятностите и времето на възникване на определени събития и резултати. Първоначално се събират данни. За да направите това, можете да използвате следния алгоритъм:

1. Определят се съставът и продължителността на фазите на жизнения цикъл;
2. Предвиждат се ключови събития, които ще засегнат (или могат да променят) по-нататъшното развитие;
3. Определя се времето на тяхното възникване;
4. Формулират се всички възможни решения, които се разглеждат като опции за ключови събития;
5. Определя се вероятността за тяхното приемане;
6. Очаквана стойност на етапите по текущи цени.

На получените данни е напълно възможно да се изгради дърво на решенията. Тя ще съдържа възли, които се считат за ключови събития. По същество това са точките на решение. Към тях се присъединяват клонове - това са определени работи, които имат за цел да постигнат определен резултат. Изграждането на дърво на решения ви позволява да изчислите вероятността за всеки избран сценарий. Освен това се обръща внимание на други фундаментално важни показатели, които са необходими за анализ на риска и за приемане на ефективни управленски действия. Трябва да се отбележи, че този метод обикновено се използва за проекти, които имат няколко възможни варианта. Всъщност в противен случай схемата става твърде обемна, което затруднява изчисляването на оптималното решение и избирането на необходимите данни. Разбиране за това как да се направи дърво на решенията трябва вече да се формира. Нека разгледаме примерите.

Инвестиционни проекти

Най-добрият начин за изясняване на дървото на решенията е пример от живота. Затова е по-добре да започнем с него, а не с абстрактна математика. Да предположим, че имаме избор между три инвестиционни проекта. Ние ги обозначаваме като IP1, IP2 и IP3. Да предположим, че за тяхното изпълнение е необходимо да се инвестират съответно 200, 300 и 500 милиона рубли. Очакваната печалба е 100, 200 и 300 милиона рубли. Съществува риск от загуба на пари. Вероятността за такъв сценарий е 10%, 5% и 20% за всяка от опциите. Какво е по-добре да изберете? Намирането на чисто математически отговор е доста трудно. Но с използването на дърво на решенията, тази задача е много по-лесна. Първоначално е необходимо да се направи дърво на решенията на инвестиционния проект. След като се изгради, започваме да го изследваме чрез обратен анализ. Трябва да отидете на снимката отдясно наляво. Влизайки в кръговете, трябва да поставим в тях математическите стойности на очакванията за плащанията. В нашия случай резултатът ще изглежда така:

1. 100 * 0.9 - 200 * 0.1 = 70;
2. 200 * 0.95 - 300 * 0.05 = 175;
3. 300 * 0.8 - 500 * 0.2 = 140.

Въз основа на изчисленията е лесно да се види, че IP2 е най-полезен за нас. А сега нека се потопим в математиката и да разгледаме някои абстрактни проблеми на дървото на решенията.

Най-простият пример

В този случай ще имаме само две опции - „не“ или „да“. Или на езика на булевата логика ще имаме 0 или 1. Разбирането на такъв пример за дърво на решения може да бъде трудно, така че ще използваме „не“ или „да“. Да предположим, че ни се предлага да работим за 160 рубли на час. Можем да кажем „не“ и след това нищо няма да се промени. Или казваме „да“, а след това, след като работим малко, можем да усетим как в джоба ни става по-тежък за 160 рубли. Можете леко да усложните модела и в случай на съгласие да добавите продължение. Например - работи усилено? Ако “да”, тогава плащане от 300 рубли, ако “не”, тогава оставаме на същото ниво от 160.

Разработване на стратегии за жизнено поведение

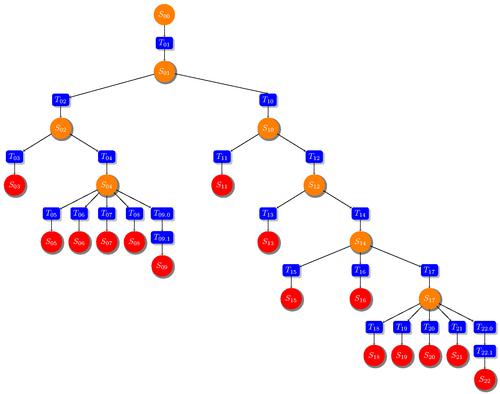
На много хора може да изглежда, че примерът на дърво на решенията се използва само за големи инвестиции и абстрактни математически изследвания. Но това не е така. Можете, разбира се, да запомните теорията. И можете да го приемете и да спечелите. Сега ще разгледаме формулата, която Жан-Пол Гети предложи, наречена „Как да станем богати“. Тя се изразява накратко: „Ставай рано“, „Работай усилено“, „Намери петрола“. Да разгледаме моделирането на последователността от решения:

1. Трябва да избираме между „Стани рано“ и „Късно заспиване“. Това е най-простият избор.
2. Трябва да избираме между „Трудни” и „След ръкави”. Това е и най-простият избор.
3. В същото време събитието "Намерено масло" може да се случи с определена вероятност. Неговата стойност зависи от последователността на нашите решения.

Ако намерихме петрол, тогава станахме богати. Няма намерени депозити - това означава, че има само загуби, разходи за търсене. И ако спите късно и работите небрежно, тогава не можете дори да търсите масло. Най-предпочитаният вариант е „Ставай рано“ и „Работай усилено“.

Търсим петрол

А сега за изчисленията. Разглежданият пример за дърво на решенията е по-добре обяснен с помощта на таблици. Да предположим, че работим оптимално. Тогава нашата опция:

Както виждате, най-печелившата опция предлага доста добри перспективи. Възможно ли е тази таблица да се използва изцяло, за да видите този пример? Да, и не е толкова трудно, колкото изглежда на пръв поглед:

Този пример на дърво на решенията ясно ни показва, че ключът към успеха е трудна работа. Размерът на работния ден може да ни доближи до целта да станем богати и да увеличим размера на държавата. Въпреки че, разбира се, данните тук са доста обобщени, но се надяваме, че общата мисъл е разбираема.

Подобряване на примера

Някой може да спори - добре, дървото на решенията е полезно. Но разглежданите варианти са твърде преувеличени, а използването им в реална ситуация е доста проблематично. Това мнение има право да съществува, но само за тези, които не разбират. Дървото на решенията може да бъде доста сложно и по-гъвкаво. Ето защо ще подобрим малко количеството на петрола. И този път трябва да вземем предвид възвращаемостта. Да предположим, че средствата за търсене на петрол се изразходват незабавно. Ако намерим минерал, тогава всички инвестиции, направени в проучването, веднага ще се изплатят. Приходите ще дойдат след две години. Както виждате, имаме разпръснати приходи и плащания през целия период от време. И ние трябва да внесем всички суми до наличните пари. Да предположим, че процентът на дисконтиране е 20%, тогава формулата ни за човек, който работи усилено и ставане рано, ще изглежда така: (0.1 * 10 000 000) / 1.22 + 0.9 (-200 000) = 514 444. За други варианти на дейност стойностите ще бъдат: 157,222, - 128,555, и - 200 000 рубли. Съгласен съм, това е по-скоро обосновка за проекта! Въпреки факта, че нивата на доходите са паднали, възможността да се работи упорито и да стават рано все още е най-ефективна. Тогава как да спим късно не привлича. И какво решение е полезно за нас, както в живота, така и в изчисленията?

Загрейте например

Ние предлагаме на читателите да консолидират своите знания. Да предположим, че имаме док. Той произвежда P1 продукти в размер на 1 хил. Единици. Ръководителят на DOK счита, че пазарът на стоки P2 се разширява. Проведени са проучвания, които позволяват да се установят предложените варианти за развитие: P1mak = 1000; P1min = 5000; P2mak = 8000; P2min = 4000. Тук min и мак е вероятността за търсене на определено количество стоки. Това означава, че хиляда P1 не е проблем за изпълнение. Но 5000 може да не успее. Вероятността за търсене е: C1mak = 0.7; C1min = 1-C1mak = 0.3; S2mak = 0.6; C2min = 1 - C2mak = 0.4. За единица стока P1 реализираме печалба в размер на 1 парична единица. За А2 тази цифра е 0.9. Но има проблем - минималното търсене за двата продукта надхвърля съществуващия и наличния капацитет на МТК. Какви ще са разходите (сега равни на К), за да ги удвоите за паралелно производство в еквивалент, ако:

1. разходите са К = 0.4 * 103 парични единици;
2. еквивалентно количество P1 = 1000 и P2 = 900;
3. максималното и текущото търсене за P1 и P2 са съответно: (K1mak = 2 * 103; K1min = 1.4 * 103) и (K2mak = 1.2 * 103; K2min = 0.8 * 103).

И при наличието на такива данни е необходимо да се определи дали е препоръчително да се заменят произвежданите продукти и да се развие капацитет.

Решаване на проблеми

Трудно ли е да го разбера сам? Е, малък намек - можете да използвате алгоритъма, който е бил използван в примера с масло. За тези, които не могат да я овладеят, ще бъде написано решение. Първоначално установяваме последиците от нашите решения за производството на един тип (Р1 или Р2). След това разгледайте опцията и с двете. За да направим това, ние отхвърляме ирационалните действия за развитие на капацитета и изтъкваме данните за възможните печалби отделно в колоната. Вземаме под внимание вероятността от търсене и оценяваме средната ефективност в клоновете. Ако изчислим, ще видим, че при продължително производство на P1 продуктите е по-изгодно за нас в развитието на мощности и едновременното производство, отколкото прехода към един P2. Въпреки, че това е, ако минималните очаквания. А какво да кажем за максималното търсене? В този случай трябва да начертаем друг клон, който да разгледа това решение. За да изчислим неговата ефективност, обобщаваме първата и втората опции и изваждаме разходите за удвояване на капацитета. И се оказва, че това е най-печелившото решение. В резултат на това стигаме до заключението, че е необходимо да се развият капацитети и да се осигури едновременното освобождаване на Р1 и Р2.

Задайте цели

Това е дървото на решенията. Примери за решаване на проблемите на риска ни позволяват да разберем този метод и да го възприемем. Разбира се, в началото може да има някои трудности, но те се решават успешно чрез практика. Книгите по математика, иконометрия, кибернетика и редица други дисциплини могат да помогнат в това.

Възможност за автоматизиране

Методите за вземане на решения имат ясна структура. Следователно компютърните технологии могат да работят съвсем лесно с тях. Като друг пример, процесът на издаване на заем в банка. В същото време, за един компютър, дървото на решенията се представя под формата на логическа конструкция „ако ... тогава ...“ Макар и между другото, той се основава и на този принцип за хората, но при взаимодействие с технологиите е необходимо да се концентрира върху това. Да предположим, че първата стъпка е въпросът за възрастта. Ако човек е на по-малко от четиридесет години, те питат за неговото образование и заплати. Още - има ли къща. Отговорът е да - ние издаваме заем. Отрицателен - питайте за нивото на доходите. По-малко от 20 хиляди рубли на месец - ние отказваме. Това става бързо и ефективно.

заключение

Ако има няколко поведения и сценарии, трябва да използвате дърво на решения, за да намерите най-добрата ситуация. Това ще позволи въвеждането на цялата налична информация и изчисления на хартия и подобряване на ефективността на вземането на решения.