Концепцията на матрицата и основните дефиниции

Такава концепция като матрица се използва и се появява в разделите на висшата математика. Най-често се намира в системата от линейни уравнения. И така, каква е основната концепция на матрицата? За да разберем това, не е необходимо да бъдем математически гений.

Матрицата е нещо, което е система от числа mn, които в математиката са написани под формата на таблици, в които m са редовете и n са колоните. На неговото пресичане има елементи. Размерът на матрицата зависи от броя на редовете и колоните.

Първоначално се разглеждаше триъгълна матрица, но тя не е удобна за решаване на сложни уравнения, затова в математиката се използва правоъгълен аналог. Такава система се счита за удобна за решаване на проблема.

Откъде идва матрицата

Ако говорим за първото споменаване, концепцията за матрицата идва от Китай, или по-скоро тя е свързана с "магически квадрати". Тези таблици се считат за амулети заради числата върху тях. По това време нямаше нито самото понятие за матрицата, нито начините за нейното разрешаване. В някои племена тя определя степента на родство, така че хората да разберат дали могат да се оженят или не.

Но самата концепция е въведена в началото на 19 век от Джеймс Силвестър, който е английски математик. Различни учени работят върху теорията на матриците, създавайки комплекс от решения за трудни алгебрични проблеми.

Матрицата и нейните основни типове

И така, по-рано се разглеждаше концепцията за матрица. Видовете матрици са представени по-долу:

• Малки букви. Той се състои от един ред, т.е. този тип матрица има броя на редовете точно m = 1, но броят на колоните е произволен.
• А колона. Този сорт се състои само от една колона, но може да съдържа и няколко реда. За този вид матрица има свой универсален вход. Той показва, че елементите, които са в скоби, трябва да бъдат написани като колона. Освен това тя спестява не само място, но и време.
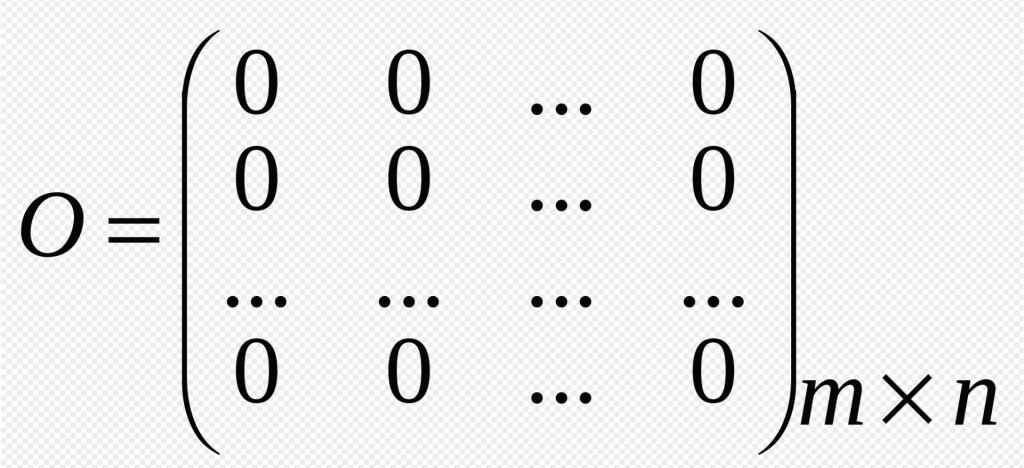
• Нулева матрица Тази форма съществува, когато всички нейни елементи са равни на 0. Те обозначават този тип матрица "О" Този елемент също получи името си поради факта, че в смятане той има сходни функции с нула в теорията на числата.
• Square. Този тип матрица е най-разпространен, разликата му е в това, че има еднакъв брой колони и редове. Когато два елемента са свързани в различни краища на колоната, получаваме основния диагонал. В тази връзка диагоналната таблица е разделена на няколко системи:

а) Диагонал. Този тип квадратна матрица, която не включва елементите, принадлежащи към основния диагонал.

б) Единична. Този тип диагонал се състои само от една единица. При всичко това всяка такава матрица е скаларна.

в) Скалар. Това е типът, където главният диагонал се състои от един и същ номер.

г) Стрелка. Това е вид квадратна матрица, в която почти всички елементи са нула, но компонентите, които съставят първата колона, както и тези, свързани с диагонала и първия ред, не са равни на нея.

• Binary. Този тип таблица се състои от нули и единици.
• Матрицата на Паскал - в този вид матрица всички елементи се състоят от числа, принадлежащи към триъгълника със същото име.
• Tridiagonal. В този вид матрица, ненулевите елементи се намират на три диагонали, които включват основния и над и под.

Матрица на ранга

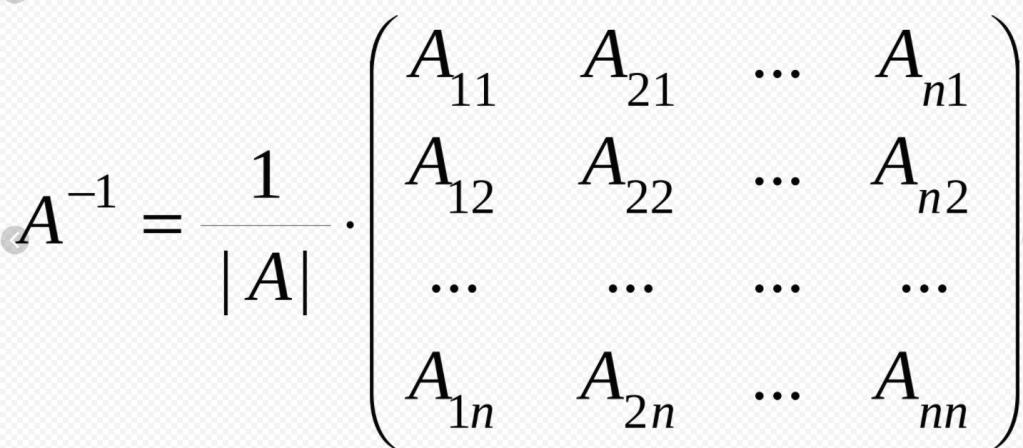
След като научихме, че тя има различни типове, е необходимо да кажем за следното понятие: рангът на матрицата. Под това се разбира броя на независимите линейни колони или броя на независимите линейни редове. Също така, рангът на всяка матрица е редът на непълнолетните, който е най-високият, неговият детерминант е ненулев.

Рангът е обозначен с rang A, но се намира ранг A. И двете понятия се считат за правилни, така че при различни изписвания това няма да се счита за грешка. Основното нещо е да не забравяме, че рангът на редовете винаги е равен на ранга на колоните.

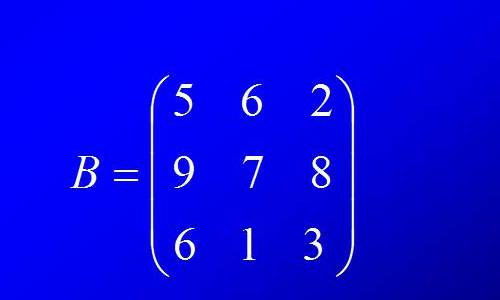
Действия върху матрицата

Матрицата е универсална система за решаване на алгебрични проблеми, върху които се извършват различни действия. Те включват умножаване на две матрици, добавяне, умножение по число и други матрици.

Изпълнявайки множество действия в алгебра, системата от различни матрици помага да се намери по-лесен начин за решаване на проблемите. Това отнема по-малко време и помага да не се изгубите в много действия.

Операциите, свързани с матрицата, се използват не само в математиката, но и във физиката и химията.