Въртящо движение и ъглова скорост на твърдо вещество
В тази статия ще разгледаме физичните величини, които характеризират въртеливото движение на тялото: ъглова скорост, ъглово изместване, ъглово ускорение, въртящ момент.
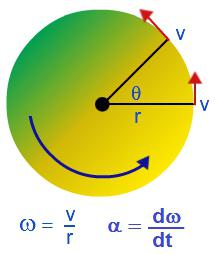
Едно твърдо тяло е съвкупност от твърдо свързани материални точки. Когато едно твърдо тяло се върти около някоя ос, отделните материални точки, от които тя се добавя, се движат по кръгове с различни радиуси.
За определен период от време, например, по време на което тялото прави една революция, отделните материални точки, които съставляват твърдо тяло, ще преминават различни пътища, следователно, отделните точки ще имат различни линейни скорости. Опишете въртенето на твърдо вещество, използвайки линейните скорости на индивида материални точки - трудно.
Ъглово изместване
Въпреки това, като се анализира движението на отделните материални точки, може да се установи, че през същия период от време всички те се обръщат около оста под същия ъгъл. Това означава, че за да се опише въртенето на твърдо тяло, е удобно да се използва такава физическа величина като ъгловото изместване:
φ = φ (t).
Ъгловата скорост и ъгловото ускорение
Въртящото движение може да се характеризира с ъгловата скорост: ω = ∆φ / ∆t.
Ъгловата скорост характеризира скоростта на въртене на тялото и е равна на съотношението на промените в ъгъла на въртене към времето, през което е настъпило. Измерени в радиани в секунда: [ω] = rad / s.
Ъгловата скорост на въртене е свързана с линейната скорост със следното съотношение: v = Rω, където R е радиусът на кръга, по който тялото се движи.
Ротационно движение тялото се характеризира с друга физична величина - ъглово ускорение, което е равно на съотношението на промяната на ъгловата скорост към времето, през което е настъпило: ε = /ω / .t. Единицата за измерване на ъгловото ускорение: [ε] = rad / s 2 .
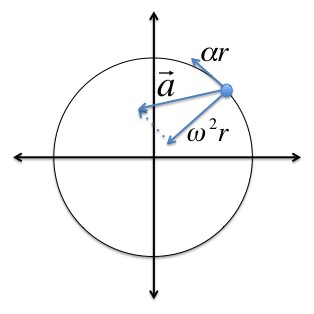
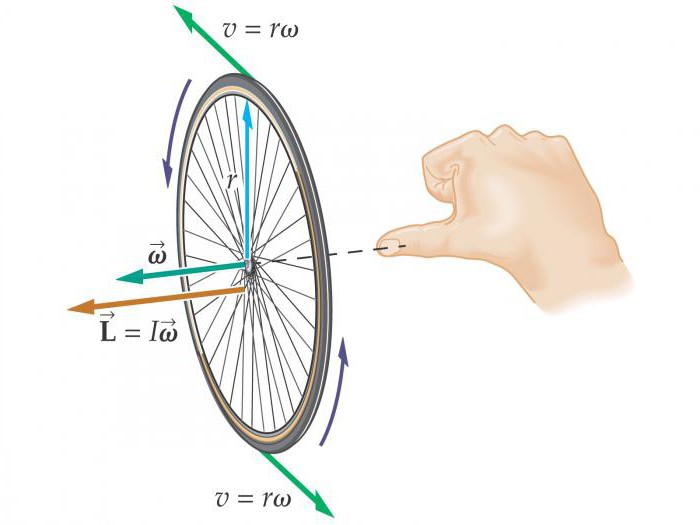
Ъгловата скорост и ъгловото ускорение са псевдовектори, посоката на които зависи от посоката на въртене. Тя може да бъде определена от правилото на десния винт.
Единно въртеливо движение
Равномерното въртеливо движение се извършва с постоянна ъглова скорост и се описва със следните уравнения: ε = 0, ω = const, φ = + 0 + ωt, където is 0 е началната стойност на ъгъла на въртене.
Равномерно ускорено въртеливо движение
Равномерно ускореното въртеливо движение настъпва с постоянно ъглово ускорение и се описва със следните уравнения: ε = const, ω = ω 0 + εt, φ = + 0 + ω 0 t + εt 2/2.
По време на въртене на твърдо вещество центростремително ускорение всяка точка от това тяло може да бъде намерена, както следва: c = v 2 / R = (ωR) 2 / R = ω 2 R.
Когато се ускори въртенето на твърдо тяло, можете да намерите тангенциалното ускорение на неговите точки по формулата: t = /V / =t = ∆ (ωR) / =t = R (/ω / )t) = Rε.
Момент на сила
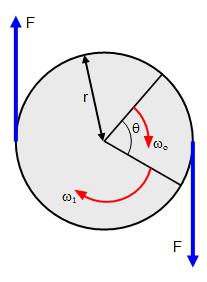
Ако, като се има предвид физически проблем, се занимаваме не с материална точка, а с твърдо тяло, тогава действието на няколко сили върху него, приложено към различни точки на това тяло, не може да бъде сведено до действието на една единствена сила. В този случай, помислете за момента на силите.
Моментът на сила се нарича продукт на силата върху рамото. Това е векторна величина и се намира по формулата: M = RFsinα, където α е ъгълът между векторите R и F. Ако има няколко моменти на сили, действащи върху тялото, тогава тяхното действие може да бъде заменено с тяхната резултатна, векторна сума от тези моменти: M = M 1 + M 2 + ... + M n .
Експериментите и опитът показват, че под действието на момент на сила, ъгловата скорост на тялото се променя, т.е. тялото има ъглово ускорение. Нека да разберем как ъгловото ускорение на материалната точка (набор от материални точки) зависи от прилагания въртящ момент: F = mɑ, RF = Rma = R 2 mβ, β = M / mR 2 = M / I, където I = mR 2 е моментът на инерцията на материала точка. Имайте предвид, че инерционният момент на тялото зависи както от масата на тялото, така и от местоположението на тази маса спрямо оста на въртене.
Примери за решаване на проблеми
Задача 1. Роторът на центрофугата е 2 • 10 4 об / мин. След изключване на двигателя, завъртането му спира след 8 минути. Намерете ъгловото ускорение, както и броя на оборотите, които роторът прави от момента на изключване на двигателя, докато спре, като се има предвид, че движението на ротора се ускорява равномерно.
решение
Да намерим ъгловото ускорение, като се има предвид, че ъгловата скорост с равномерно ускорено движение се описва с уравнението: ω (t) = ω 0 - εt.
Следователно, като се има предвид, че в края на движението скоростта е нула, намираме: ε = ω 0 / t = 2πn / t.
Прехвърляйки тези задачи в единица SI на единици (n = 333 rev / s; t = 480 s) , получаваме: ε = 2π333 / 480 = 4.36 (rad / s 2 ).
Ъгълът на въртене на ротора на центрофугата по време на време t ще бъде: t (t) = + 0 + ω 0 t + εt 2/2. Y чете израза за ъгловото ускорение и факта, че = 0 = 0 , намираме: φ (t) = ω 0 t / 2 = πnt.
Броят на оборотите на ротора през това време ще бъде: N = φ (t) / 2π = πnt / 2π = nt = 8 • 10 4 (vol.).
Отговор: ъгловото ускорение е 4,36 rad / s 2 ; броят на оборотите, направени от ротора от момента на изключване на двигателя до пълното му спиране, е 8 • 10 4 об. / мин.
Задача 2. Диск с маса 1 kg и радиус 20 cm се върти с честота 120 rpm. след минута. Под действието на спирачното устройство на ръба на диска започна да действа сила на триене 10 N. Намерете време да спрете диска, след като започна да действа силата на триене.
решение
Намерете спирачния момент, действащ върху диска: M = RF.
Намерете ъгловото ускорение на диска: ε = M / I = FR / mR 2 = F / mR.
Намерете времето, за което дискът ще спре: t = ω 0 / ε , където ω 0 е началната ъглова скорост на диска, която е равна на 2πv.
Изчисляваме: t = 2πv / ε = 2πvmR / F = 6.28 • 2 • 1 • 0.2 / 10 = 2.5 (s).
Отговор: времето за спиране е 2,5 секунди.