Материална точка: определение, ценности, примери и решаване на проблеми

Каква е материалната точка? Какви физически величини са свързани с него, за което обикновено се въвежда понятието за материална точка? В тази статия ще обсъдим тези въпроси, ще дадем примери за проблеми, които са свързани с обсъжданата концепция, и ще говорим за формулите, използвани за тяхното решаване.

дефиниция

И така, каква е материалната точка? Различни източници дават определение в малко по-различен литературен стил. Същото се отнася и за учителите в университетите, колежите и образователните институции. Въпреки това, според стандарта, материална точка се нарича тяло, чиито размери (в сравнение с размерите на референтната рамка) могат да бъдат пренебрегнати.

Връзка с реални обекти

Изглежда, как може да вземете човек, колоездач, кола, кораб и дори самолет като материална точка, с която се занимават най-вече с физични проблеми, когато става въпрос за механиката на движещо се тяло? Нека погледнем по-дълбоко! За да определите координатите на движещо се тяло по всяко време, е необходимо да знаете няколко параметъра. Това е първоначалната координата и скоростта на движение, и ускорението (ако то, разбира се, се случва), и времето.

Какво е необходимо за решаване на проблеми с материални точки?

Координатните отношения могат да бъдат намерени само чрез свързване към координатната система. Нашата планета се превръща в такъв вид координатна система за кола и друго тяло. И в сравнение с неговия размер, размерът на тялото наистина може да бъде пренебрегнат. Съответно, ако вземем тялото като материална точка, неговата координата в двуизмерна (триизмерно) пространство може и трябва да се намери като координат на геометрична точка.

Движението на материалната точка. задачи

В зависимост от сложността задачите могат да придобият определени условия. Съответно, въз основа на дадените условия, можем да използваме определени формули. Понякога, дори и с целия арсенал от формули, все още не е възможно да се реши проблемът, както се казва, "на главата". Затова е изключително важно не само да се познават кинематичните формули, които са свързани с материалната точка, но и да могат да се използват. Тоест, да се изрази желаната стойност и да се уеднакви системата от уравнения. Ето основните формули, които ще приложим в процеса на решаване на проблеми:

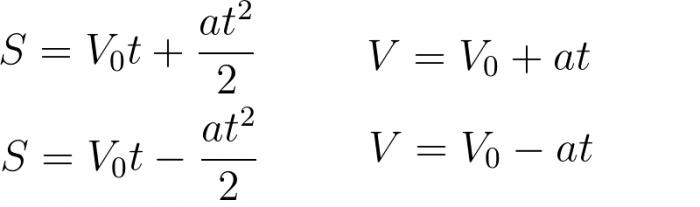
Проблем номер 1

Колата, стояща на стартовата линия, внезапно започва да се движи от неподвижна позиция. Разберете кога ще ускори до 20 метра в секунда, ако ускорението е 2 метра в секунда на квадрат.

Просто искам да кажа, че тази задача е на практика най-простото нещо, което студентът може да очаква. Думата „на практика“ стои тук с причина. Работата е там, че може да бъде по-лесно просто да замениш директни стойности с формули. Първо трябва да изразим времето и след това да направим изчисления. За да решим проблема, се нуждаем от формулата за определяне на моментната скорост (моментната скорост е скоростта на тялото в даден момент във времето). Той има следната форма:

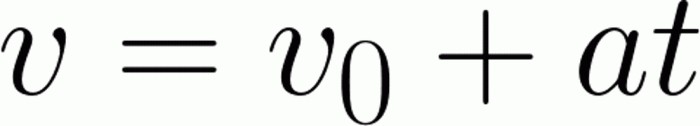
Както можем да видим, от лявата страна на уравнението имаме моментна скорост. Ние абсолютно не се нуждаем от нея там. Затова правим прости математически операции: оставяме продукта за ускорение за известно време от дясната страна и прехвърляме началната скорост наляво. В същото време трябва внимателно да следвате знаците, тъй като един неправилно оставен знак може радикално да промени отговора на задачата. След това леко усложняваме израза, освобождавайки се от ускорението от дясната страна: разделяме го. В резултат на това отдясно трябва да имаме чисто време, отляво, двустепенен израз. Цялото нещо е просто заменено, за да изглежда познато. Остава само да замести стойностите. Така се оказва, че автомобилът ще ускори за 10 секунди. Важно: решихме проблема, ако приемем, че в колата има материална точка.

Проблем номер 2

Материалната точка започва аварийно спиране. Определете каква е била началната скорост по време на аварийното спиране, ако 15 секунди минаха преди пълното спиране на тялото. Ускорението се приема равно на 2 метра в секунда на квадрат.

Задачата по принцип е доста сходна с предишната. Но има и някои от техните нюанси. Първо, трябва да определим скоростта, която обикновено наричаме начална скорост. Това означава, че в определен момент започва отброяването на времето и изминатото разстояние от тялото. Скоростта в този случай наистина ще попадне в това определение. Вторият нюанс е знак за ускорение. Припомнете си, че ускорението е векторно количество. Следователно, в зависимост от посоката, тя ще промени своя знак. Наблюдава се положително ускорение, ако посоката на скоростта на тялото съвпада с посоката му. Просто казано, когато тялото се ускорява. В противен случай (т.е. в нашата спирачна ситуация) ускорението ще бъде отрицателно. Тези два фактора трябва да бъдат разгледани, за да се реши този проблем:

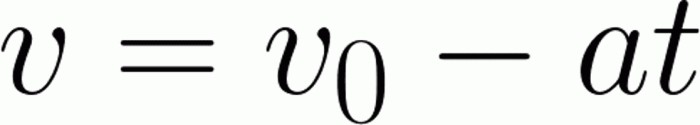
Както миналия път, първо изразяваме стойността, от която се нуждаем. За да избегнем бъркотията със знаци, оставяме първоначалната скорост там, където е. С противоположния знак прехвърляме към другата част на уравнението продукт на ускорение по време. След завършването на спирането, крайната скорост е 0 метра в секунда. Подменяйки тези и други стойности, лесно намираме началната скорост. Тя ще бъде равна на 30 метра в секунда. Лесно е да се забележи, че познаването на формули не е толкова трудно да се справиш с най-простите задачи.

Проблем номер 3

В определен момент диспечерите започват да проследяват движението на въздушен обект. Скоростта му в този момент е 180 километра в час. След период от време, равен на 10 секунди, скоростта му се увеличава до 360 километра в час. Определете разстоянието, изминато със самолет по време на полета, ако полетното време е било 2 часа.

Всъщност в широк смисъл тази задача има много нюанси. Например, ускорението на самолета. Ясно е, че нашето тяло не може да се движи по принцип по права линия. Това означава, че той трябва да излети, да вдигне скорост, а след това, на определена височина, някакъв сегмент от разстоянието трябва да се движи по права линия. Отклоненията не се вземат предвид, както и забавянето на самолета по време на кацане. Но това не е наша работа в този случай. Затова ще решим проблема в рамките на училищните знания, обща информация за кинематичното движение. За да решим проблема, се нуждаем от следната формула:

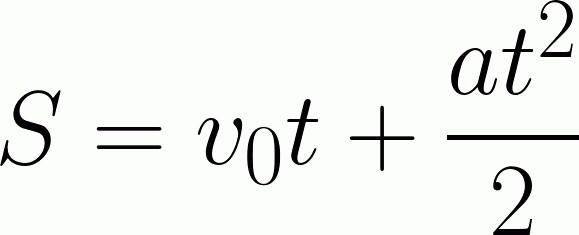
Но тук имаме затруднение, за което говорихме по-рано. Познаването на формули не е достатъчно - трябва да можете да ги използвате. Тоест, изведете една стойност, използвайки алтернативни формули, намерете я и я заменете. Когато преглеждате първоначалната информация, която е налична в задачата, веднага става ясно, че за решаването му просто няма да работи. Нищо не се казва за ускорението, но има информация за това как скоростта се е променила за определен период от време. Така че можем да намерим ускорението от себе си. Вземете формулата за намиране на моментна скорост. Тя има поглед

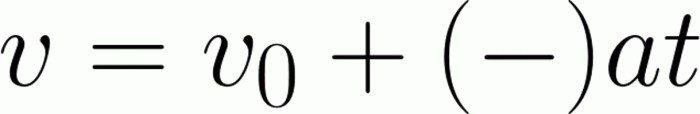
Ускорението и времето остават в една част, а началната скорост се прехвърля на другата. След това, като разделим двете части за известно време, освобождаваме дясната страна. Тук можете веднага да изчислите ускорението, като замените директните данни. Но е много по-целесъобразно да се изрази по-нататък. Получената за ускорението формула се замества с основната. Там можете леко да намалите променливите: в числителя времето се дава в квадрата, а в знаменателя - в първа степен. Следователно, от този знаменател можете да се отървете от. Е, тогава - просто заместване, тъй като няма какво повече да се изрази. Отговорът трябва да бъде следният: 440 километра. Отговорът ще бъде различен, ако преведете стойности в друго измерение.

заключение

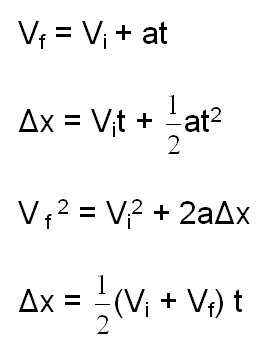
И така, какво открихме в хода на тази статия?

1) Материалната точка е тяло, чиито размери могат да бъдат пренебрегнати в сравнение с размера на референтната система.

2) За решаване на проблеми, свързани с материална точка, има няколко формули (дадени в статията).

3) Знакът на ускорението в тези формули зависи от параметъра на движението на тялото (ускорение или забавяне).