Линейни уравнения: формули и примери. Неравенства и тяхното решение
Ученето за решаване на уравнения е една от основните задачи, които алгебрата поставя пред учениците. Започвайки от най-простите, когато се състои от едно неизвестно, и се придвижваме към все по-сложни. Ако действията, които трябва да се извършат с уравненията от първата група, не бъдат разбрани, ще бъде трудно да се справим с другите.
За да продължите разговора, трябва да се съгласите с нотацията.
| Име на стойността | Неговото обозначение |
| променлив | x, y |
| произволен номер | a, b, c |
Общ изглед на линейно уравнение с едно неизвестно и принципа на неговото решение
Всяко уравнение, което може да доведе до запис от този тип:
a * x = в ,
наречена линейна . Това е обща формула. Но често в задания, линейни уравнения са написани имплицитно. След това трябва да извършите идентични трансформации, за да получите общоприетия запис. Тези действия включват:
Ad
- отварящи скоби;
- преместване на всички термини с променлива към лявата страна на уравнението, а останалите на дясно;
- с подобни условия.
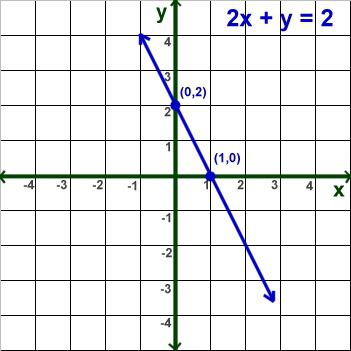
В случай, когато неизвестна стойност е в знаменателя на една дроб, е необходимо да се определят нейните стойности, при които изразът няма да има смисъл. С други думи, необходимо е да се знае областта на уравнението.
Принципът, с който се решават всички линейни уравнения, се свежда до разделяне на стойността от дясната страна на равенството с коефициента пред променливата. Това означава, че "x" ще бъде равно на / a.
Специални случаи на линейно уравнение и техните решения
По време на разсъжденията такива моменти могат да възникнат, когато линейните уравнения вземат един от специалните типове. Всеки от тях има специфично решение.
В първата ситуация:
a * x = 0 , освен това a ≠ 0.
Решението на такова уравнение винаги ще бъде x = 0.
Във втория случай "а" приема стойност, равна на нула:
0 * x = 0 .
Отговорът на това уравнение ще бъде произволен брой. Тоест, той има безкраен брой корени.
Третата ситуация изглежда така:
0 * x = in , където в. 0.
Това уравнение няма смисъл. Защото корените, които го удовлетворяват, не съществуват.

Общ изглед на линейно уравнение с две променливи
От името му става ясно, че вече има две неизвестни количества. Линейните уравнения с две променливи изглеждат така:
a * x + v * y = s .
Тъй като в записа има две неизвестни, отговорът ще изглежда като чифт числа. Това не е достатъчно, за да посочите само една стойност. Това ще бъде непълен отговор. Двойката величини, при която уравнението се превръща в идентичност, е решение на уравнението. Освен това отговорът винаги е първият, който записва променливата, която върви по-рано по азбучен ред. Понякога казват, че тези номера го удовлетворяват. Освен това, такива двойки могат да бъдат безкраен брой.
Ad
Как да решим линейно уравнение с две неизвестни?
За да направите това, просто вземете всяка двойка числа, която се оказва вярна. За простота, можете да приемете едно от неизвестните, за да бъде равно на всяко просто число и след това намери втория.
При решаването често е необходимо да се извършват действия за опростяване на уравнението. Те се наричат трансформации на идентичност. Освен това, следните свойства винаги са валидни за уравнения:
- всеки термин може да бъде прехвърлен в противоположната част на равенството чрез замяна на неговия знак с обратното;
- лявата и дясната страна на всяко уравнение могат да бъдат разделени на един и същи номер, ако не е равен на нула.

Примери за задачи с линейни уравнения
Първата задача. Решете линейни уравнения: 4x = 20, 8 (x - 1) + 2x = 2 (4 - 2x); (5х + 15) / (х + 4) = 4; (5х + 15) / (х + 3) = 4.
В уравнението, което е първо в този списък, е достатъчно просто да разделим 20 на 4. Резултатът ще бъде 5. Това е отговорът: x = 5.
Третото уравнение изисква да се извърши трансформацията на идентичността. Тя ще се състои в разкриването на скоби и привеждането на такива термини. След първото действие уравнението приема формата: 8x - 8 + 2x = 8 - 4x. След това трябва да прехвърлите всички неизвестни на лявата страна на равенството, а останалите на дясно. Уравнението ще изглежда по следния начин: 8x + 2x + 4x = 8 + 8. След намаляване на такива термини: 14x = 16. Сега тя изглежда същата като първата и нейното решение е лесно. Отговорът е х = 8/7. Но в математиката трябва да се разпредели цялата част от нея грешна фракция. Тогава резултатът ще се трансформира, а "x" ще бъде равен на едно цяло и едно седмо.
Ad
В останалите примери променливите са в знаменателя. Това означава, че първо трябва да знаете на какви стойности са дефинирани уравненията. За това трябва да изключите числата, при които знаменателите се обръщат към нула. В първия пример това е “-4”, а във второто е “-3”. Това означава, че тези стойности трябва да бъдат изключени от отговора. След това трябва да умножите двете страни на уравнението с изразите в знаменателя.
Отваряйки скобите и даващи подобни термини, в първото от тези уравнения получаваме: 5x + 15 = 4x + 16, а във второто 5x + 15 = 4x + 12. След преобразуванията, решението на първото уравнение е х = -1. Вторият е равен на "-3", което означава, че последният няма решения.
Втората задача. Решете уравнението: -7x + 2y = 5.
Да предположим, че първото неизвестно x = 1, тогава уравнението приема формата -7 * 1 + 2y = 5. След като прехвърли фактора “-7” в дясната част на уравнението и промени знака на плюс, се оказва, че 2u = 12. Следователно, y = 6. Отговор: едно от решенията на уравнението е х = 1, у = 6.
Ad

Общ изглед на неравенството с една променлива
Тук са представени всички възможни ситуации за неравенства:
- a * x> in;
- a * x <v;
- a * x ≥ in;
- a * x ≤v.
По принцип изглежда като най-простото линейно уравнение, само знакът на равенството се заменя с неравенство.
Идентични правила за преобразуване на неравенството
Както линейните уравнения, така и неравенствата могат да бъдат модифицирани според определени закони. Те се свеждат до следното:
- всеки литерален или цифров израз може да бъде добавен към лявата и дясната страна на неравенството, като знакът на неравенството остава същият;
- възможно е също да се умножи или раздели със същото положително число, отново знакът не се променя;
- когато се умножи или раздели с едно и също отрицателно число, равенството ще остане вярно, при условие че знакът на неравенството се обърне.

Общ изглед на двойните неравенства
В проблемите могат да бъдат представени следните проблеми на неравенствата:
- в <a * x <s;
- в ≤ a * x <s;
- в <a * x ≤ s;
- в ≤ a * x ≤ c.
Двойно се нарича, защото е ограничено от признаци на неравенство от двете страни. Тя се решава, като се използват същите правила като обикновените неравенства. А намирането на отговора се свежда до редица идентични трансформации. Докато не се получи най-простото.
Особености на решението на двойните неравенства
Първият от тях е изображението на координатната ос. Няма нужда да се използва този метод за прости неравенства. Но в трудни случаи може просто да е необходимо.
Ad
За образа на неравенството е необходимо да се отбележат по оста всички точки, които са се появили по време на разсъжденията. И двете са невалидни стойности, които се обозначават с пунктирани точки и стойностите от неравенствата, получени след трансформации. Тук също е важно правилно да се очертаят точките. Ако неравенството е строго, тоест <or>, тогава тези стойности се пробиват. При слаби неравенства точките трябва да бъдат оцветени.
Тогава е необходимо да се обозначи значението на неравенствата. Това може да стане с излюпване или дъги. Тяхното пресичане ще покаже отговора.
Втората характеристика е свързана с неговия запис. Ето две възможности. Първият е крайното неравенство. Вторият е под формата на пропуски. Случва се с него да възникнат трудности. Интервалите за отговор винаги изглеждат като променлива със знак за принадлежност и скоби с числа. Понякога има няколко празнини, а след това между скобите трябва да напишете символа “и”. Тези знаци са както следва: ∈ и ∩. Интервалите също играят роля. Първият кръг се определя, когато точката е изключена от отговора, а правоъгълната включва тази стойност. Знакът за безкрайност е винаги в скоби.
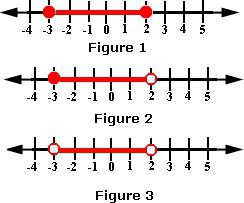
Примери за разрешаване на неравенствата
1. Решете неравенството 7 - 5x ≥ 37.
След прости преобразувания се оказва: -5x ≥ 30. Разделяйки се на “-5” можете да получите следния израз: x ≤ -6. Това е отговорът, но може да бъде написан по друг начин: x ∈ (-∞; -6].
2. Решаване на двойното неравенство -4 <2x + 6 ≤ 8.
Първо, трябва да извадиш навсякъде 6. Оказва се: -10 <2x ≤ 2. Сега трябва да се разделим на 2. Неравенството ще изглежда така: -5 <x ≤ 1. След като е изобразен отговорът на числовата ос, може веднага да се разбере, че резултатът ще бъде от -5 до 1. И първата точка е изключена, а втората е включена. Това означава, че отговорът на неравенството е: x ∈ (-5; 1]).