Неправилни фракции: как да се научим да решаваме примери с тях?

Когато думата "фракции" много мръсотия се изпълняват. Защото помня училището и задачите, които бяха решени по математика. Това беше отговорност, която трябваше да бъде изпълнена. И какво, ако се отнасяме към задачите, съдържащи правилни и неправилни фракции, като пъзел? В крайна сметка много възрастни решават цифрови и японски кръстословици. Разберете правилата и всичко. Така е и тук. Човек трябва само да схване теорията - и всичко ще падне на мястото си. И примерите ще се превърнат в начин за обучение на мозъка.

Какви видове фракции съществуват?

За начало какво е то. Фракцията е число, което има част от единица. Тя може да бъде написана в две форми. Първият се нарича обикновен. Това е така, че има хоризонтална или наклонена черта. Тя е равна на знака за разделяне.

В такъв запис номерът над тирето се нарича числител, а под него знаменателят.

Сред обикновените разпределят правилните и нередовни фракции. В първия числител по модул винаги е по-малък от знаменателя. Ето защо те се наричат ​​погрешни, защото имат всичко обратното. Стойността на правилната фракция винаги е по-малка от единица. Докато грешното винаги е по-голямо от това число.

Все още има смесени числа, т.е. тези, които имат части и части.

Вторият вид запис е десетичен. За нея е отделен разговор.

Каква е разликата между нередовни и смесени числа?

В основата си нищо. Това е просто различен запис от същия номер. Неправилните части след прости действия лесно стават смесени числа. И обратно.

Всичко зависи от конкретната ситуация. Понякога в задачите е по-удобно да се използва неправилна фракция. А понякога е необходимо да се преведе в смесен номер и след това примерът ще бъде решен много лесно. Следователно, какво да се използва: неправилни фракции, смесени числа - зависи от наблюдението на решаването на проблема.

Смесеният номер също се сравнява със сумата на целочислената част и дробната. А вторият винаги е по-малък от един.

Как да се представи смесен брой под формата на неправилна фракция?

Ако искате да извършите действие с няколко номера, които са записани в различни форми, тогава трябва да ги направите еднакви. Един от методите е да се представят числата като нередовни фракции.

За тази цел трябва да изпълните действията според този алгоритъм:

• умножете знаменателя с целочислената част;
• добави към резултата стойността на числителя;
• напишете отговора над линията;
• знаменателят оставя същото.

Ето примери за това как да напишем неверни части от смесени числа:

• 17 '= (17 х 4 + 1): 4 = 69/4;
• 39 ½ = (39 х 2 + 1): 2 = 79/2.

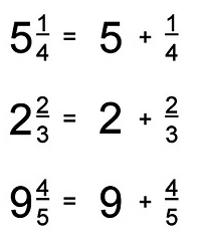
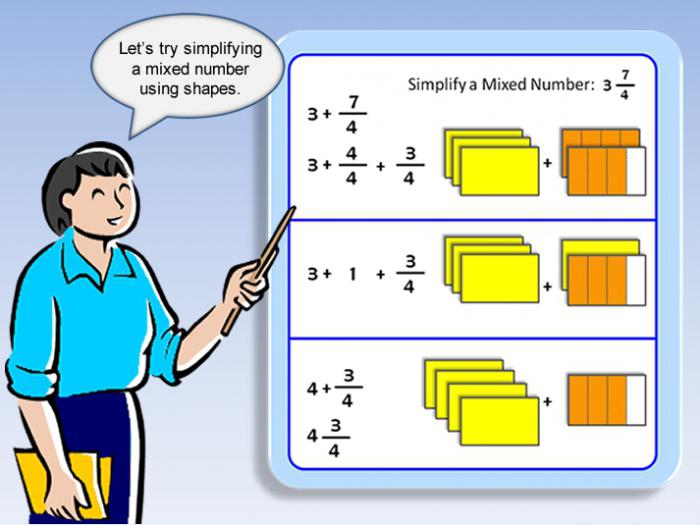
Как да напишем неподходяща фракция под формата на смесен номер?

Следващата техника е противоположна на горното. Тоест, когато всички смесени числа се заменят с неправилни части. Алгоритъмът на действията ще бъде както следва:

• разделят числителя с знаменателя, докато се получи баланс;
• напишете частното на мястото на цялата част на смесената;
• останалата част трябва да се постави над линията;
• делителят ще бъде знаменателят.

Примери за такава трансформация:

76/14; 76:14 = 5 с остатък от 6; отговорът е 5 числа и 6/14; дробната част в този пример трябва да бъде намалена с 2, ще бъде 3/7; крайният отговор е 5 3/7.

108/54; след разделяне, част 2 се получава без остатък; Това означава, че не всички неправилни части могат да бъдат представени като смесен брой; отговорът е цяло число - 2.

Как да превърнем цяло число в нередовна фракция?

Има ситуации, в които такова действие е необходимо. За да получите погрешни фракции с вече известен знаменател, трябва да изпълните този алгоритъм:

• умножете цяло число с желания знаменател;
• напишете тази стойност над линията;
• знаменател на място под него.

Най-лесният вариант, когато знаменателят е един. Тогава нищо не трябва да се умножава. Достатъчно е само да напишете цялото число, дадено в примера, и да поставите модула под линията.

Пример : 5, за да направите неправилна фракция с знаменател от 3. След като умножите 5 с 3, получаваме 15. Този номер ще бъде знаменател. Фракция на отговор: 15/3.

Два подхода за решаване на задачи с различни номера

В примера е необходимо да се изчисли сумата и разликата, както и продукта и коефициента на две числа: 2 цели числа 3/5 и 14/11.

При първия подход смесеният брой ще бъде представен като неправилна фракция.

След като изпълните описаните по-горе стъпки, получавате следната стойност: 13/5.

За да разберете сумата, трябва да донесете фракцията в същия знаменател. 13/5 след умножаване по 11 ще стане 143/55. 14/11 след умножение по 5 ще приеме формата: 70/55. За да изчислите сумата, трябва само да добавите числителите: 143 и 70 и след това да запишете отговора с един знаменател. 213/55 - този неправилен дял е отговорът на проблема.

Когато се намери разликата, същите числа се изваждат: 143 - 70 = 73. Отговорът ще бъде част: 73/55.

Когато се умножават 13/5 и 14/11, не е необходимо да водим до общ знаменател. Достатъчно е да се умножат по двойки числителите и знаменателите. Отговорът ще бъде: 182/55.

Същото е и с разделянето. За правилното решение трябва да замените делението чрез умножение и завъртете разделителя: 13/5: 14/11 = 13/5 x 11/14 = 143/70.

При втория подход неправилната фракция се превръща в смесено число.

След извършване на действията алгоритъмът 14/11 ще се превърне в смесен номер с цяло число 1 и частично 3/11.

При изчисляването на сумата трябва да се добавят частично и частично частите поотделно. 2 + 1 = 3, 3/5 + 3/11 = 33/55 + 15/55 = 48/55. Окончателният отговор е 3 точка 48/55. При първия подход беше частта 213/55. Можете да проверите коректността, като го преведете в смесен номер. След като разделим 213 на 55, получаваме коефициент 3 и останалите 48. Лесно е да се види, че отговорът е правилен.

При изваждане знакът “+” се заменя с “-”. 2 - 1 = 1, 33/55 - 15/55 = 18/55. За да проверите отговора от предишния подход, трябва да преведете в смесен номер: 73 е делимо на 55 и получаваме коефициент 1 и остатък 18.

Смесването на номера е неудобно за намиране на работа и коефициент. Винаги е препоръчително да отидете на грешни фракции.