Как да направим уравнение по права линия на две точки: двумерни и триизмерни случаи
Правата линия в геометрията е един от най-важните елементи, тъй като от нея са събрани много фигури, както на равнината, така и в пространството. Достатъчно е да се нарече триъгълник, паралелограма, призма, пирамида - всички те са оформени от пресичащи се прави линии. Тази статия отговаря на въпроса как да се направи линейно уравнение с две точки.
Уравнение на линия за двумерни и триизмерни случаи
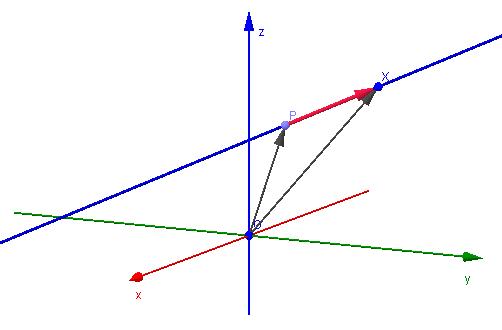
Преди да пристъпим към обсъждане на въпроса как да съставим уравнение на права линия от две точки, трябва да разберем какво е заложено.
Уравнението на права линия се разбира като равенство, свързано с приетата координатна система, и всички стойности на променливите, които го удовлетворяват, трябва да лежат върху една права линия. В двумерни и триизмерни случаи това уравнение може да се определи както следва:
Q = P + α * u¯
Тук Q е координатите на произволна точка от линията, Р е координатите на определена точка, принадлежаща на линията, u¯ е векторът на посоката, а е всяко реално число. Векторът на посоката u е успореден на правата линия. Този израз се нарича параметрично-векторно уравнение.
В двумерния случай всяка точка на равнината е еднозначно определена от две координати x и y, така че можете да напишете уравнението на линията във формата:
(x; y) = (x 0 ; y 0 ) + α * (a; b)
Където (x 0 ; y 0 ) са координатите на известната точка на линията, (a; b) са координатите на управляващия вектор. В параметрична форма това уравнение може да бъде пренаписано като система от две уравнения:
х = х 0 + а * а;
y = y 0 + α * b.
Изразявайки алфа параметъра и приравнявайки получените равенства, стигаме до формата:
y = b / a * x + (y 0 -x 0 * b / a) или
y = A * x + C, където A = b / a, C = (y 0 - x 0 * b / a)
Полученият израз е познат на всеки ученик. Тя се нарича общо уравнение на линия в равнината.
В пространството всяка точка се дава не от две, а от три координати, следователно нейното параметрично-векторно уравнение приема формата:
(x; y; z) = (x 0 ; y 0 ; z 0 ) + α * (a; b; c)
Параметрично-векторното уравнение е удобно да се използва, когато трябва да се направи уравнение на права линия, минаваща през две точки.
Права линия и две точки
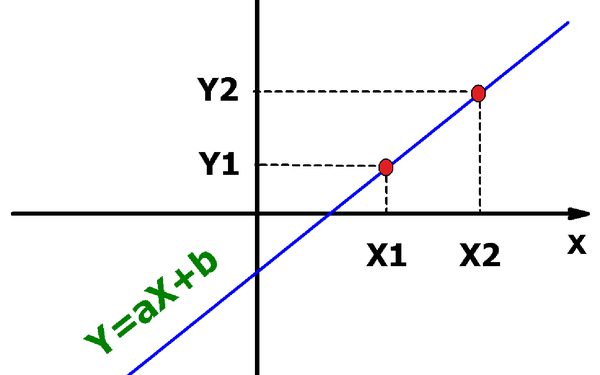
Сега разгледайте въпроса директно. Как да направим директно уравнение с две точки? Първо, получаваме уравнение на равнината и след това го обобщаваме за триизмерния случай.
Да предположим, че има две точки в равнината P (x 1 ; y 1 ) и Q (x 2 ; y 2 ). Ако вземем разликата между координатите на точките, ще получим вектор, насочен от единия към другия. Този вектор е равен на:
PQ¯ (x 2 -x 1 ; y 2 -y 1 )
В този случай, PQ¯ се насочва от P (началото на насочения сегмент) към Q (неговия край). Тъй като и двете точки принадлежат на линията, векторът PQ¯ принадлежи на нея. Това означава, че може да се счита за ръководство. Уравнението на права линия приема формата:
(x; y) = (x 1 ; y 1 ) + α * (x 2 -x 1 ; y 2 -y 1 )
Тук взехме точка П. Ако го заместим с точка Q, тогава уравнението няма да се промени.
Как да направим уравнение на права линия в пространството, използвайки две точки? Обобщавайки получената формула за равнината, получаваме:
(x; y; z) = (x 1 ; y 1 ; z 1 ) + β * (x 2 -x 1 ; y 2 -y 1 ; z 2 -z 1 )
Другата буква за параметъра е взета, за да покаже независимостта на това и предишните уравнения.
Пример за решаване на проблема
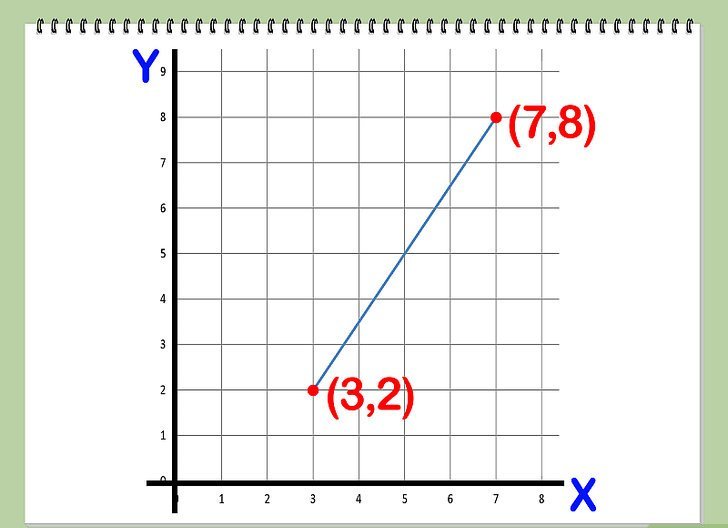
След като разбрахме как да направим пряко уравнение за две точки, даваме пример за използване на придобитите знания за двумерния случай.
Да предположим, че има точки в равнината (3; -4) и (0; 7). Необходимо е да се направи директно уравнение чрез две точки.
Изчислява се координатите на водещия вектор:
(0-3; 7 - (- 4)) = (-3; 11)
Параметрично-векторното уравнение има формата:
(x; y) = (3; -4) + α * (- 3; 11)
Отворете го и го въведете в общата форма:
x = 3 - 3 * α => α = (х-3) / (- 3);
у = -4 + 11 * α => α = (y + 4) / 11;
(x-3) / (- 3) = (y + 4) / 11 =>
y = -11 / 3 * x + 7.
Получихме уравнението в обичайната (обща) форма. Можете да проверите неговата валидност, като замените координатите на двете точки от състоянието на проблема.