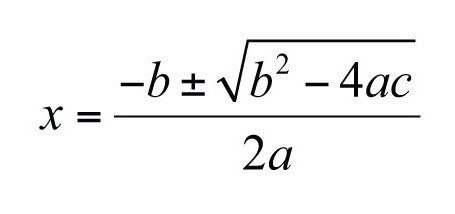Как да намерим корена на уравнението: линейно, квадратично, кубично?

Уравненията в математиката са толкова важни, колкото глаголите на руски език. Без способността да се намери коренът на уравнението е трудно да се твърди, че студентът е усвоил курс по алгебра. Освен това, за всеки от техните видове съществуват свои специфични решения.

Какво е това?

Уравнението е два произволни израза, съдържащи променливи с равен знак между тях. Освен това, броят на неизвестните количества може да бъде произволен. Минималният брой е един.

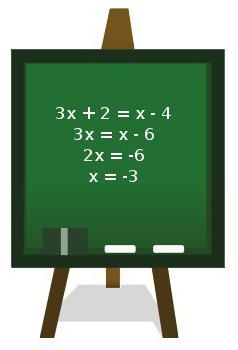
За да го решим, трябва да разберем дали има корен на уравнението. Това е число, което го превръща в правилно равенство. Ако не, тогава отговорът е твърдението, че "няма корени". Но може да бъде обратното, когато отговорът е множество числа.

Какви уравнения съществуват?

Линеен. Той съдържа променлива, чиято степен е равна на единица.

• Square. Променливата стои с мощност 2, или трансформацията води до такава степен.
• Уравнение с най-висока степен.
• Рационално фракционно. Когато променливата е в знаменателя на фракцията.
• С модул.
• Нерационалното. Това е така, което съдържа алгебричен корен.

Как се решава линейното уравнение?

Тя е основната. За тази цел всички останали се стремят да водят. Тъй като е лесно да се намери коренът на уравнението.

• Първо, трябва да извършите възможни трансформации, т.е. да разширите скобите и да дадете подобни термини.
• Преместете всички мономи с променлива в лявата страна на уравнението, оставяйки свободните термини в дясно.
• Въведете подобни термини във всяка част на уравнението, които трябва да бъдат решени.
• В полученото равенство в лявата му половина ще има произведение на коефициент и променлива, а в дясната половина ще има число.
• Остава да се намери коренът на уравнението, разделяйки числото отдясно на коефициента пред неизвестното.

Как да открием корените на квадратичното уравнение?

Първо, трябва да се сведе до стандартен формуляр, т.е. да се отворят всички скоби, да се въведат подобни термини и всички мономи трябва да се преместят в лявата страна. От дясната страна на равенството трябва да остане само нула.

• Използвайте дискриминантната формула. Коефициент на коефициента преди неизвестното със степен "1". Умножете свободния мономер и числото пред променливата в квадрата с числото 4. Извадете продукта от получения квадрат.
• Оценете стойността на дискриминанта. Тя е отрицателна - решението е завършено, тъй като няма корени. Равен на нула - отговорът е един номер. Положителни - две стойности на променливата.

• 

  Намерете двата корена на уравнението според формулата, в която квадратен корен от дискриминанта трябва да се извади или добави към отрицателния коефициент на променливата в първата степен. След това разделяйте с двойно коефициента, който стои пред квадрата на неизвестното. (В случай на равенство на дискриминанта, нула ще трябва да се добави или извади, така че двата корена ще съвпаднат.)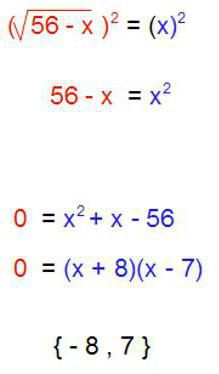

Как да решим кубично уравнение?

Първо намерете корена на уравнението x. Тя се определя от метода на подбор от числата, които са делители на свободния термин. Този метод е удобен за разглеждане на конкретен пример. Нека уравнението е: x ³ - 3x ² - 4x + 12 = 0.

Свободният му термин е 12. Тогава дивизорите, които трябва да бъдат проверени, са положителни и отрицателни числа: 1, 2, 3, 4, 6 и 12. Търсенето може да се извърши на номер 2. Дава истинското равенство в уравнението. Това означава, че лявата му страна се оказва нула. Така че номер 2 е първият кубичен корен уравненията.

Сега трябва да разделите оригиналното уравнение с разликата между променливата и първия корен. В конкретен пример това е (x - 2). Една проста трансформация води до числител към такава факторизация: (x - 2) (x + 2) (x - 3). Същите фактори на числителя и знаменателя се намаляват, а останалите две скоби в разкритието дават просто квадратно уравнение: х ² - х - 6 = 0.

Тук откриваме двата корена на уравнението съгласно принципа, описан в предишния раздел. Това са числата 3 и -2.

Така че, конкретно кубично уравнение има три корена: 2, -2 и 3.

Как се решават системите линейни уравнения?

Тук се предлага метод за елиминиране на неизвестни. Тя се състои в изразяване на едно неизвестно чрез друго в едно уравнение и подмяна на този израз в друг. Освен това, решението на система от две уравнения с две неизвестни винаги е двойка променливи.

Ако променливите в тях са обозначени с буквите x ₁ и x ₂ , тогава можем да извлечем от първото уравнение, например x ₂ . След това се заменя във втория. Извършва се необходимата трансформация: разкриване на скоби и принуда от страна на подобни членове. Оказва се, че е просто линейно уравнение, чийто корен е лесен за изчисляване.

Сега се върнете към първото уравнение и намерете корена на уравнението x ₂ , използвайки полученото уравнение. Тези два числа са отговорът.

Обикновено съвети

За да сте сигурни в получения отговор, препоръчваме ви винаги да правите проверка. Не е необходимо да пишете.

Ако едно уравнение е решено, тогава всеки от неговите корени трябва да бъде заменен в първоначалното равенство и да получи същите числа в двете му части. Всичко се сближи - правилното решение.

При работа със системата е необходимо да се заменят корените във всяко решение и да се извършат всички възможни действия. Оказва се, че е правилното равенство? Така че решението е правилно.