Как да се проведе пълно функционално проучване

В тази статия ще разгледаме схемата за изучаване на функция, както и примери за изследвания на крайности, монотонност и асимптоти на тази функция.

схема

1. Функция за зона на съществуване (DHS).
2. Пресечната точка на функцията (ако има такава) с осите на координатите, знаците на функцията, паритета, периодичността.
3. Точки на прекъсване (техния род). Непрекъснатост. Вертикални асимптоти.
4. Монотонност и точки на екстремум.
5. Точки на инфлексия Изпъкналостта.
6. Изследването на функцията в безкрайност, върху асимптоти: хоризонтално и наклонено.
7. Построяване.

Проучване на монотонността

Теорема. Ако функцията g е непрекъсната на [a, b] , диференцирана с (a; b) и g '(x) ≥ 0 (g' (x) ≤0) , xê (a; b) , тогава g се увеличава (намалява) с [a, b] .

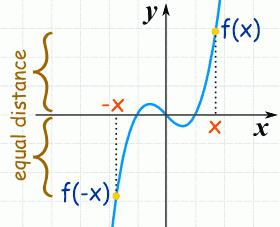
например:

у = 1: 3x ³ - 6: 2x ² + 5x.

DHS: xR

y '= x ² + 6x + 5.

Намерете интервали на постоянни знаци y ' . Тъй като y ' е елементарна функция, тя може да променя знаците само в точки, където се превръща в нула или не съществува. Нейният DHS: xR .

Намерете точките, производната на които е 0 (нула):

y '= 0;

х = -1; -5.

Така, y нараства на (-∞; -5] и на [-1; + ∞), y спускане до [1; 2] .

Екстремни изследвания

T. x _{0 се} нарича максималната точка (max) на множеството А на функцията g, когато стойността g (x ₀ ) ≥ g (x), xеA , се приема като функция в тази точка.

Т. x _{0 се} нарича минималната точка (min) на функцията g на множеството А, когато най-малката g (x ₀ ) ≤ g (x), xеA се приема като функция в тази точка .

На множеството А максималните точки (max) и минималните (min) се наричат ​​екстремални точки g . Такива крайности се наричат ​​и абсолютни крайности на множеството ,

Ако x ₀ е точка на екстремум на g в дадена област, тогава x ₀ се нарича точка на локален или локален екстремум (max или min) от g.

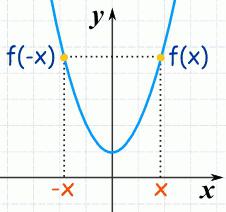
Теорема (изисква се условие). Ако x ₀ е точката на екстремума на (локалната) функция g , тогава дериватът не съществува или е равен в тази r. 0 (нула).

Определение. Критичните точки са точки с несъществуваща или равна на 0 (нула) производна. Тези данни са подозрителни за екстремума.

Теорема (условие № 1). Ако функцията g е непрекъсната в определено съседство на t. X ₀ и знакът променя производната си при прехода, тогава дадената точка е на екстремума на g .

Теорема (условие № 2). Нека функцията в даден район да бъде диференцируема два пъти и g '= 0, и g' '> 0 (g' '<0) , след това тази точка е точката на максимална (макс.) или минимална (мин) функция.

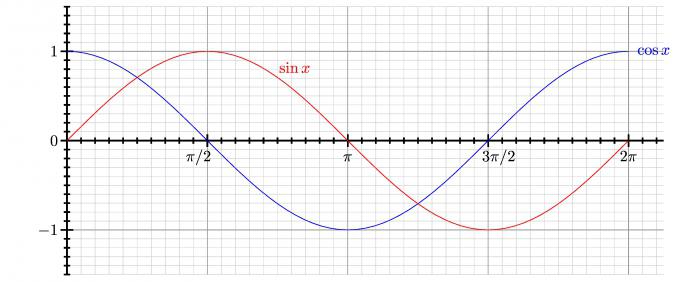
Изследване на издутините

Функцията се нарича изпъкнала надолу (или вдлъбната) на интервала (a, b), когато графиката на функцията не е по-висока от секунданта на интервала за всеки x с (a, b), който минава през тези точки .

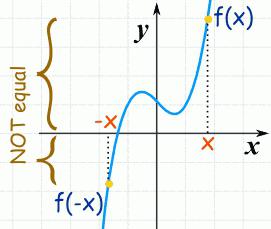
Функцията ще бъде изпъкнала строго надолу върху (a, b) , ако - графиката се намира под секунда върху пропастта.

Функцията се нарича изпъкнала нагоре (изпъкнала) на интервала (a, b) , ако за всяка точка t с (a, b) графиката на функцията на интервала не е по-ниска от секунданта, преминаващ през абсцисите в тези точки ,

Функцията ще бъде строго изпъкнала нагоре по (a, b ), ако - графиката на интервала се намира над секунданта.

Ако дадена функция в даден район е точка е непрекъснато и след t х ₀ функцията променя изпъкналостта при прехода, тази точка се нарича точка на инфлексия на функцията.

Асимптотен тест

Определение. Права линия се нарича асимптота g (x), ако на безкрайно разстояние от началото на координатите се приближава точката на графа на функциите: d (M, l).

Асимптотите могат да бъдат вертикални, хоризонтални и наклонени.

Вертикалната линия с уравнението x = x ₀ ще бъде асимптотата на вертикалната графика на функцията g ако в t. x _{0 е} безкрайна празнина, т.е. поне една лява или дясна граница в този момент е безкрайност.

Изследването на функцията на сегмента върху стойността на най-малката и най-голямата

Ако функцията е непрекъсната на [a, b] , тогава според теоремата на Вайерщрас има най-голямата стойност и най-малката стойност на този сегмент, т.е. има точки t, които принадлежат на [a, b], така че g (x ₁ ) ≤ g (x) <g (х2), х2Е [а, Ь]. От теоремите за монотонността и крайностите получаваме следната схема за изучаване на функция на сегмент за най-малка и най-голяма стойност.

план

1. Намерете производното g '(x) .
2. Намерете стойността на функцията g в тези точки и в краищата на сегмента.
3. Намерените стойности сравняват и избират най-малките и най-големите.

Забележка. Ако искате да изучите функцията на краен интервал (a, b) или на безкрайно (-∞; b); (-∞; + ∞) на максимална и минимална стойност, след това в плана вместо стойностите на функцията в краищата на празнината се търсят съответните едностранни граници: вместо f (a) търсят f (a +) = limf (x) , вместо f (b) търсят f (Ь). Така че можете да намерите функциите на LDU на интервала, защото в този случай не съществуват непременно абсолютни крайности.

Прилагане на деривата за решаване на приложни задачи на екстремума на определени величини

1. Тази стойност се изразява чрез други стойности от състоянието на проблема, така че да е функция само на една променлива (ако е възможно).
2. Определете периода на промяна на тази променлива.
3. Проведете изследване на функцията на интервала при максимални и минимални стойности.

Задача. Необходимо е да се изгради правоъгълна платформа, използваща решетъчни метри, срещу стената, така че от едната страна да се впише в стената, а на другите три да е оградена с решетка. В какво съотношение ще бъде най-голяма площта на такъв сайт?

S = xy е функция от 2 променливи.

S = x (a - 2x) - функция на първата променлива ; x е [0; a: 2].

S = ax - 2x ² ; S '= a - 4x = 0, xєR, x = a: 4.

S (a: 4) = a ² : 8 е най-високата стойност;

S (0) = 0.

Намерете другата страна на правоъгълника: = a: 2.

Аспектно съотношение: y: x = 2.

Отговорът е. Най-голямата площ ще бъде равна на 2/8 , ако страната, която е успоредна на стената, е 2 пъти по-голяма от другата страна.

Изследователска функция. примери

Пример 1

Има y = x ³ : (1-x) ² . Извършване на изследвания.

1. DHS: xе (-∞; 1) U (1; ∞).
2. Общата форма на функцията (нито четно, нито нечетно) не е симетрична за точката 0 (нула).
3. Признаци на функция. Функцията е елементарна, така че може да променя само знака в точките, където е 0 (нула) или не съществува.
4. Функцията е елементарна, следователно е непрекъсната в DHS: (-∞; 1) U (1; ∞).

Gap: x = 1;

limx ³ : (1- x) ² = ∞ - Прекъсване на 2-ри вид (безкрайно), така че в точка 1 има вертикална асимптота;

x = 1 е вертикалното асимптотно уравнение.

5. y '= x ² (3 - x): (1 - x) ³ ;

DHS (y '): x; 1;

x = 1 - критична точка.

y '= 0;

0; 3 - критични точки.

6. y "= 6x: (1 - x) ⁴ ;

Критично t: 1, 0;

x = 0 - m. kink, y (0) = 0.

7. limx ³ : (1 - 2x + x ² ) = ∞ - няма хоризонтална асимптота, но може да бъде наклонена.

k = 1 е число;

b = 2 е число.

Следователно има асимптота, наклонена y = x + 2 при + ∞ и при - ∞.

Пример 2

Дадено y = (x ² + 1): (x - 1). За да се направи и проучване. Създайте графика.

1. Областта на съществуване е цялата цифрова линия, с изключение на m. X = 1 .

2. y пресича OY (ако е възможно) в m. (0; g (0)) . Намиране на y (0) = -1 - т. пресичане OY ,

Откриваме точките на пресичане на графа с OX, като решим уравнението y = 0 . Коренно уравнение няма валидна, следователно тази функция не пресича OX .

3. Функцията не е периодична. Помислете за израза

g (-x) (g (x), и g (-x) -g (x) . Това означава, че това е обща функция (нито дори нечетна).

4. Т. х = 1 празнина има втори вид. Във всички останали точки функцията е непрекъсната.

5. Изследването на функцията на екстрема:

(x ² - 2x - 1): (x - 1) ² = y '

и решаване на уравнението y '= 0.

Така, 1 - √2, 1 + √2, 1 - критични точки или точки на възможен екстремум. Тези точки разделят цифровата линия на четири интервала .

Във всеки интервал дериватът има определен знак, който може да бъде зададен чрез метода на интервалите или чрез изчисляване на стойностите на производната в отделните точки. На интервалите (-∞; 1 - ) 2 ) U ( 1 + ; 2 ; ∞) положителното производно означава, че функцията расте; ако xе ( 1 - ; 2 ; 1) U (1; 1 + √2 ) , тогава функцията намалява, защото в тези интервали дериватът е отрицателен. Чрез t. X ₁ при движение (от ляво на дясно) се променя производният знак от "+" на "-", затова в този момент има локален максимум, намираме се на

y _max = 2 - 2 .2.

Когато преминавате през x _{2, той} променя производния знак от "-" на "+", следователно в този момент има местен минимум и

y _mix = 2 + 2√2.

T. x = 1 не е толкова екстремум.

6. 4: (x - 1) ³ = y ".

При (-∞; 1 ) 0> y " , следователно, на този интервал кривата е изпъкнала; ако xе ( 1 ; ∞) - кривата е вдлъбната. В точка 1 функцията не е дефинирана, следователно тази точка не е точка на инфлексия.

7. От резултатите от параграф 4 следва, че x = 1 е асимптотна вертикална крива.

Хоризонтални асимптоти липсват.

x + 1 = y е асимптотата, наклонена по тази крива. Няма други асимптоти.

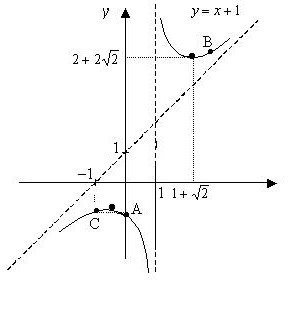
8. Като се има предвид провежданото изследване, ние изграждаме графика (виж фигурата по-горе).