Как да извършим разделението на деривати?

Когато се работи с функции, често е необходимо да се вземе предвид тяхната специфичност, извършване на събиране, умножаване или разделяне на производни. Последният от действията най-често повдига въпроси от ученика, така че този аспект трябва да бъде разгледан по-подробно.

Частно производно

Когато се извършва разделението на производните, формулата за трансформацията изглежда като разликата между производната на числителя, умножена по знаменателя и производната на знаменателя, умножена с числителя и разделена на квадрата на знаменателя. Трябва да се има предвид, че стойността в долната част на фракцията не трябва да е равна на нула. При решаването на първите примери, трансформацията на производното на коефициент често предизвиква проблем, така че е най-добре тази формула да е пред очите ви:

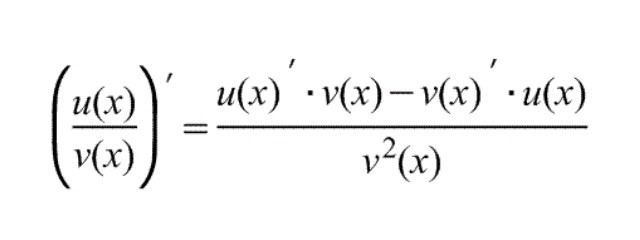
Благодарение на тази формула е възможно да се даде пример в по-проста форма, която може да бъде разделена на таблични функции на производните, след което няма да е трудно да се реши този проблем.

Пример за решение

Като пример, демонстриращ решението, където се извършва делението на производните, заслужава да се разгледа следното:

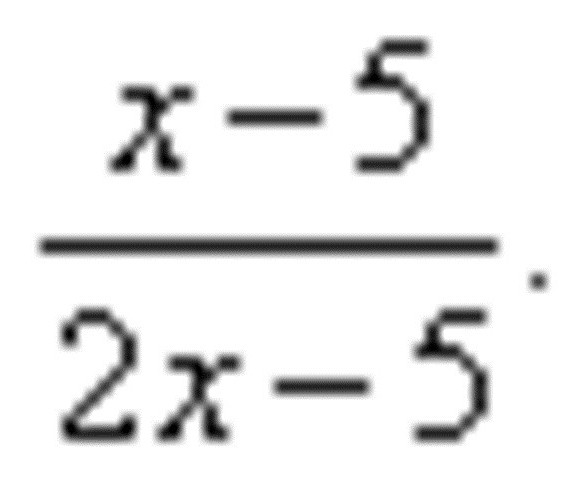
Според задачата е необходимо да се намери производното на този израз. Използвайки формулата, която опростява разделянето на производните, преобразуваме оригиналния пример в следната форма:

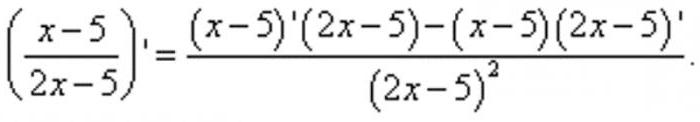
В резултат на това числителят се оказа две производни на таблична форма, чиито стойности могат да бъдат изчислени без допълнителни преобразувания. В първия случай резултатът ще бъде един, а във втория - два. Подставяйки изчислените данни в пример, получаваме фракция, в която остава само да извърши прости изчисления в числителя, получавайки крайния резултат:

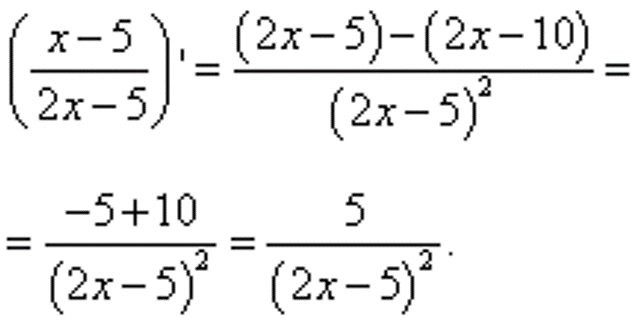
Малки трикове

Преди да приложите формулата, трябва да разгледате отблизо разделението на дериватите. В някои случаи фракцията може да бъде опростена, така че формулата, дадена в началото, може да е ненужна или да стане по-опростена. Фракцията може да бъде опростена по няколко начина, включително разделяне на числителя с знаменателя, за да се определи целочислената част, както и умножаване на двете части на фракцията с едно и също ненулево число - тази техника често се използва, когато има ирационалност под знака на деривата.

Заслужава да се отбележи, че преди да се наложи първо да проверите пример за решение. За да направите това, трябва да намерите областта на допустимите стойности (DHS) и ако тя съществува без да създавате несигурност от различен тип, можете да продължите с изчисленията.