Как да се изчисли обемът на топката и други нюанси в изчисленията
Преди да започнете да изучавате концепцията за топка, какъв е обемът на топка, помислете за формулите за изчисляване на нейните параметри, трябва да си припомните концепцията за кръг, изучаван по-рано в хода на геометрията. В края на краищата, повечето от действията в триизмерно пространство са подобни или произтичат от двуизмерна геометрия, коригирана за появата на третата координатна и третата степен.
Какво представлява кръгът?
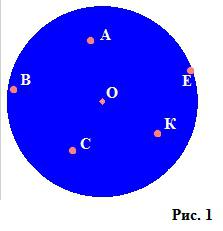
Кръг е фигура на декартова равнина (показана на фигура 1); Най-често дефиницията звучи като "мястото на всички точки в равнината, разстоянието, от което до дадена точка (център) не надвишава определено неотрицателно число, наречено радиус."
Както се вижда от фигурата, точката О е центърът на фигурата, а съвкупността от абсолютно всички точки, които запълват окръжността, например А, В, С, К, Е, не са по-далеч от определен радиус (не се простират извън кръга, показан на фигурата). . 2).
Ако радиусът е нула, кръгът се превръща в точка.
Проблеми с разбирането
Учениците често бъркат тези понятия. Лесно е да се запомни, като се направи аналогия. Обръчът, който децата усукват в часовете по физическо възпитание, е кръг. Разбирайки това или си спомняйки, че първите букви на двете думи са „О“, децата ще разбират разликата между тях.
Въвеждане на понятието "топка"

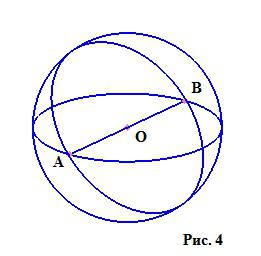
Топка е тяло (фиг. 3), ограничено от сферична повърхност. Каква „сферична повърхност“ ще стане ясно от неговата дефиниция: това е геометричното разположение на всички точки на повърхността, разстоянието, от което до дадена точка (център) не надвишава определено неотрицателно число, наречено радиус. Както виждаме, понятията за кръг и сферична повърхност са сходни, само пространствата, в които са разположени, се различават. Ако нарисуваме топка в двуизмерно пространство, получаваме окръжност, границата на която е окръжност (границата е сферична повърхност). На фигурата се вижда сферична повърхност с радиуси OA = OB.
Топка е затворена и отворена
В векторни и метрични пространства се разглеждат и две понятия, свързани със сферична повърхност. Ако топката включва тази сфера сама по себе си, тогава тя се нарича затворена, а ако не, тогава топката е отворена. Това са по-напреднали понятия, те се изучават в институциите с въвеждането на анализа. За проста, дори домашна употреба, тези формули, които се изучават в хода на стереометрията на 10-11 класове, са достатъчни. Именно такива концепции са достъпни за почти всеки средно образован човек, който ще бъде обсъден по-нататък.
Концепции, които трябва да знаете за следните изчисления
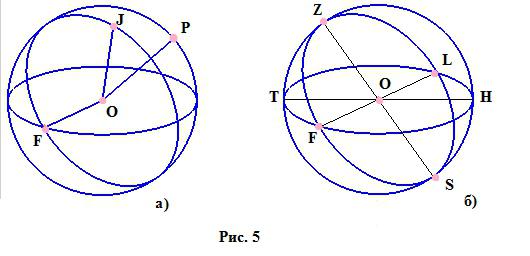
- Радиус и диаметър.
- Радиусът на топчето и неговият диаметър се определят по същия начин като кръг.
- Радиус - сегмент, свързващ всяка точка на границата на топката и точката, която е центъра на топката.
- Диаметър - сегмент, свързващ две точки на границата на топката и преминаващ през неговия център. Фигура 5а ясно показва кои сегменти са радиусите на топката, а на фигура 5Ь са показани диаметрите на сферата (сегментите, преминаващи през точката О).
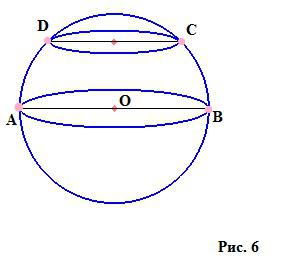
Раздели в сфера (топка)
Всяка част от сферата е кръг. Ако тя преминава през центъра на топката, тя се нарича голям кръг (кръг с диаметър АВ), останалите участъци са малки кръгове (кръг с диаметър DC).
Площта на тези кръгове се изчислява по следните формули:
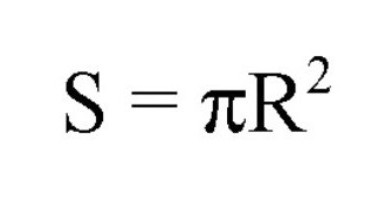
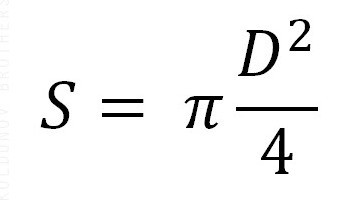
Тук S е обозначението на областта, R е радиусът, D е диаметърът. Също така присъства константа от 3.14. Но не бъркайте, че за изчисляване на площта на голям кръг, използвайки радиуса или диаметъра на сферата, и за да определите площта, са необходими размерите на радиуса на малък кръг.
Има безброй такива участъци, които преминават през две точки със същия диаметър, разположени на границата на топката. Като пример - нашата планета: две точки на Северния и Южния полюс, които са краищата на земната ос, и в геометричен смисъл - краищата на диаметъра и меридианите, които преминават през тези две точки (Фигура 7). Това означава, че броят на големите кръгове в сферата се стреми към безкрайност в число.
Части от топки
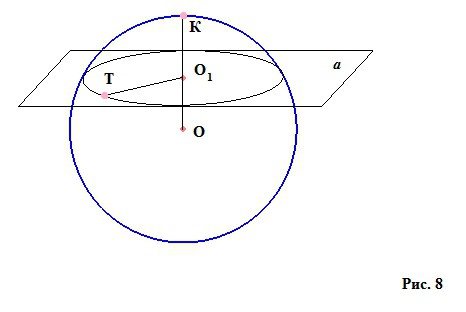
Ако отрежете сфера от сфера с помощта на определена „плоска” равнина (фигура 8), тогава тя ще се нарича сферичен или сферичен сегмент. Тя ще има височина - перпендикулярна от центъра на режещата равнина към сферичната повърхност O 1 K. Точката К на сферичната повърхност, към която идва височината, се нарича върхът на сферичния сегмент. И малък кръг с радиус O 1 T (в този случай, според фигурата, плоскостта не е преминала през центъра на сферата, но ако участъкът минава през центъра, тогава кръгът на участъка ще бъде голям), образуван при отрязването на сферата, ще се нарича основа на нашата част топка - сферичен сегмент.
Ако свържете всяка точка от основата на сферичния сегмент с центъра на сферата, ние получаваме форма, наречена "сферичен сектор".
Ако две сфери, които са успоредни една на друга, минават през сферата, тогава тази част от сферата, която е затворена между тях, се нарича сферичен слой (фигура 9, която показва сфера с две равнини и сферичен слой поотделно).
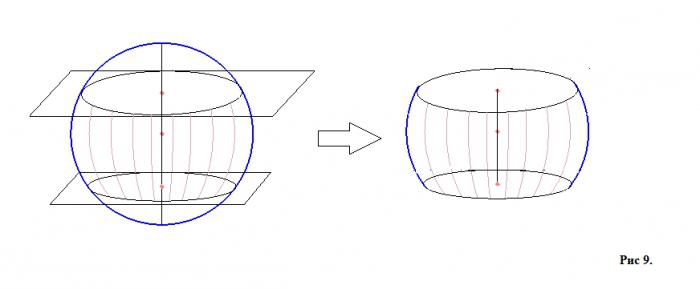
Повърхността (осветената част на фигура 9 отдясно) на тази част на сферата се нарича колан (отново, за по-добро разбиране може да се направи аналогия с земното кълбо, а именно с нейните климатични зони - арктически, тропически, умерени и др.), А кръговете на секциите ще бъдат основите топка слой. Височината на слоя е частта от диаметъра, изтеглена перпендикулярно на режещите равнини от центровете на основите. Има и концепция за сфера. Тя се формира в случая, когато равнините, които са успоредни една на друга, не пресичат сферата, а я докосват всяка точка.
Формула за изчисляване на обема на топката и нейната повърхност
Топка се формира чрез завъртане около фиксиран диаметър на полукръг или кръг. За изчисляване на различните параметри на този обект няма да са необходими твърде много данни.
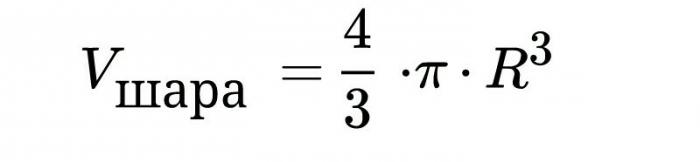
Обемът на топката, формулата за изчисляване, която е посочена по-горе, се получава чрез интеграция. Ще разберем точките.
Ние разглеждаме кръг в двумерна равнина, защото, както е споменато по-горе, кръгът е в основата на конструирането на топката. Използваме само четвъртата му част (Фигура 10). 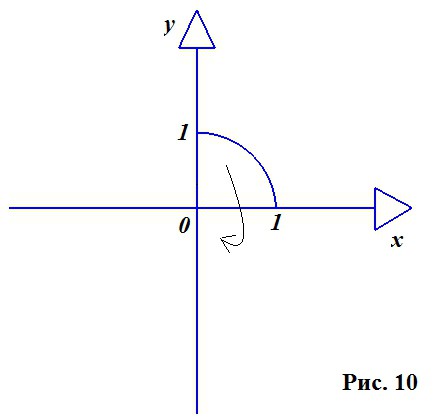
Вземете кръг с радиус на единица и център в началото. Уравнението на такъв кръг е следното: X 2 + Y 2 = R 2 . Изразяваме от тук Y: Y 2 = R 2 - X 2 . 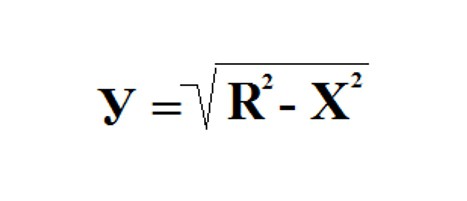
Не забравяйте да отбележите, че получената функция е неотрицателна, непрекъсната и намаляваща на сегмент X (0; R), защото стойността на X в случая, когато разглеждаме една четвърт от окръжността, лежи от нула до стойността на радиуса, т.е.
Следващото нещо, което правим, е да завъртим нашата четвърт от кръга около оста Х. В резултат на това получаваме полусфера. За да определим обема си, прибягваме до методите на интеграция.
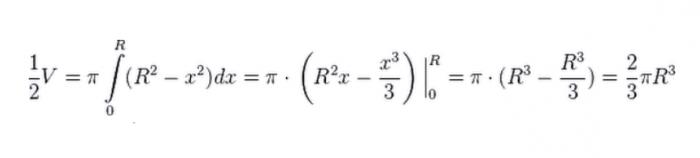
Тъй като този обем е само полусфера, удвояваме резултата, откъдето получаваме, че обемът на топката е равен на:
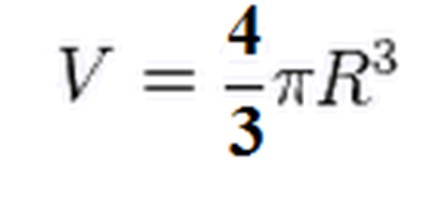
Малки нюанси
Ако е необходимо да се изчисли обемът на топката през неговия диаметър, не забравяйте, че радиусът е половината от диаметъра, и заменете тази стойност с горната формула.
Също така, формулата за обема на топката може да бъде достигната през зоната на граничещата с нея повърхност - сферата. Припомнете си, че площта на сферата се изчислява по формулата S = 4πr 2 , интегрирайки това, и стигаме до горната формула за обема на топката. От същите формули може да се изрази радиуса, ако състоянието на проблема съдържа стойност на обема.