Висша математика: равнина в пространството
Вторият след права линия важен елемент от пространствената геометрия е равнината. Възможността да се опише чрез уравнението позволява да се изчислят пространствените ъгли и височини за различни триизмерни форми. В тази статия ние даваме всички видове уравнения, които описват равнина в пространството. Също така помислете за възможните варианти за взаимно подреждане на самолетите.
Геометрична концепция на самолет
В двуизмерната геометрия равнината не се разглежда, тъй като всички проблеми се решават само в x и y координати. Когато добавим третата координатна ос z, равнината става важен геометричен елемент.
Терминът "равнина" се разбира като съвкупност от точки, всяка от които, ако е свързана, полученият вектор винаги ще бъде перпендикулярна на някой даден вектор. Този даден вектор се нарича нормален. Нормалното играе важна роля в численото описание на равнината и нейните свойства се използват за решаване на различни проблеми.
Фигурата по-долу показва три равнини в пространството (сини), които пресичат четвъртото (червено).
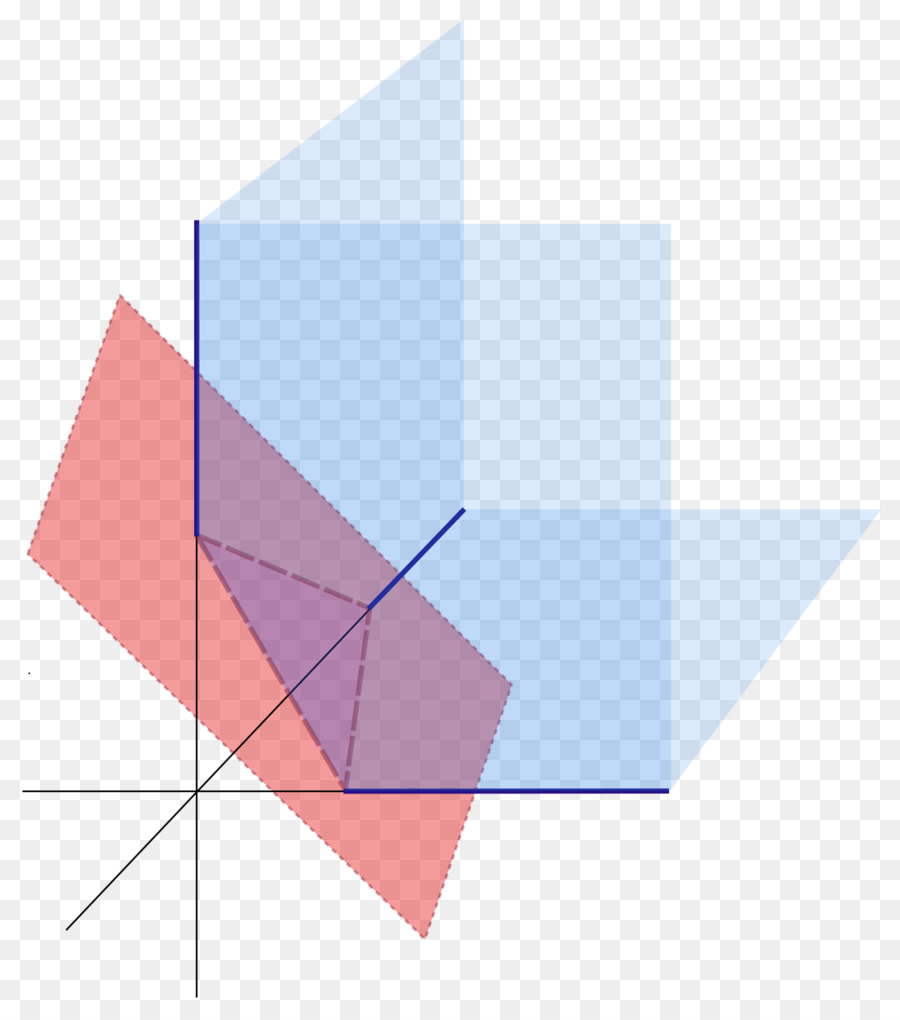
Общо уравнение
Горната дефиниция ще помогне да се получи уравнение за равнина в пространството в координатите. Да предположим, че има някаква точка с известни координати Q (x 0 ; y 0 ; z 0 ). Известно е, че то се намира в определена равнина, нормалната на която е равна на n¯ (A; B; C). Да предположим, че произволна точка M (x; y; z) също принадлежи на тази равнина. Последното означава, че векторите QM¯ и n¯ са перпендикулярни, т.е. техният скаларен продукт изчезва. Затова можем да напишем следното равенство:
(QM¯ * n¯) = 0.
Подменяйки координатите в нея и отваряйки скобите, стигаме до уравнението:
(xx 0 ) * A + (yy 0 ) * B + (zz 0 ) * C = 0 =>
A * x + B * y + C * z + D = 0, където D = -1 * (A * x 0 + B * y 0 + C * z 0 ).
Полученото уравнение за равнината се нарича общо. Той има същата форма като общото уравнение за директно уравнение на равнина. Може да се види, че коефициентите, изправени пред променливите x, y и z, не са нищо повече от координатите на перпендикулярната равнина на вектора. Той се нарича режисура.
Забележете, че ако при получаване на общо уравнение дадена точка Q е неизвестна и има само вектор на посоката n¯, тогава стигаме до уравнението за набор от паралелни равнини, които се различават само по параметъра D.
Частично уравнение
Когато се изобразяват равнини в пространството, когато са дадени специфични оси на координати, най-лесно е да се поддържат геометрични конструкции, ако има точки, където равнината пресича тези оси. Един израз, който ви позволява да намерите координатните стойности на пресечната точка на равнината с осите x, y и z, се нарича интервално уравнение. Тя може да бъде получена чрез извършване на някои математически трансформации с общо уравнение.
Да предположим, че следното уравнение е известно:
A * x + B * y + C * z + D = 0.
Прехвърлете свободния термин D в дясната страна на уравнението и след това разделете двете страни на уравнението така, че единицата да е отдясно. Имаме:
A * x + B * y + C * z = -D =>
х / (- D / A) + y / (- D / B) + z / (- D / C) = 1 или
x / p + y / q + z / r = 1, където p = -D / A, q = -D / B, r = -D / C.
Полученият израз се нарича уравнение в сегментите, а дължините на отрязаните сегменти по осите x, y и z, започвайки от точката (0; 0; 0), имат стойностите p, q и r, съответно. Това може да се провери по следния начин: ако приемем, че координатите по оста y и z са нули, тогава x се получава q. Тоест точката на пресичане с оста х има координати (p; 0; 0). По същия начин, аргументирайки, получаваме останалите две координати (0; q; 0) и (0; 0; r).
Параметрично векторно уравнение
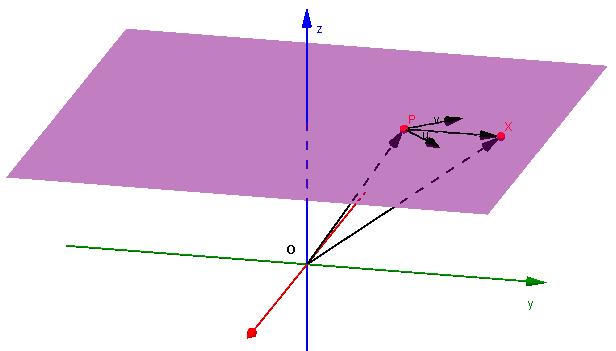
Това е третият важен тип уравнение, което често се използва и при решаването на проблеми. По-горе беше показано, че равнината е еднозначно определена от точка и нормален вектор. Възможно е обаче този геометричен двуизмерен обект да се определи по различен начин.
Да предположим, че има два копланарни вектора, които не са успоредни един на друг. Ще ги обозначим с u¯ (a 1 ; b 1 ; c 1 ) и v¯ (a 2 ; b 2 ; c 2 ). Точката Q (x 0 ; y 0 ; z 0 ) също е известна. Какво ще бъде уравнението на равнината, която минава през тази точка и два вектора?
Можете да отговорите на този въпрос, като получите уравнение като цяло. Ние обаче ще решим този проблем по друг начин. Припомнете си, че всеки вектор от равнината може да бъде разложен на два други копланарни вектора, които също принадлежат на тази равнина. Това означава, че произволен вектор QP¯, където P (x; y; z), може да бъде представен като:
QP¯ = α * u¯ + β * v¯.
Преминавайки през всички точки P на равнината, получаваме съответните параметри α и β. Дадено уравнение за равнина се нарича параметрично векторно. Често се записва в координатна форма:
(x; y; z) = (x 0 ; y 0 ; z 0 ) + α * (a 1 ; b 1 ; c 1 ) + β * (a 2 ; b 2 ; c 2 ).
Може да се види, че тази форма на писане на равнината е подобна на векторното уравнение за права линия в двумерните и триизмерните случаи.
Този израз също може да бъде написан по-ясно чрез разделяне на променливите:
х = х 0 + а * а 1 + р * а2 ;
y = y 0 + α * b 1 + β * b 2 ;
z = z 0 + α * c 1 + β * c 2 .
Тези три уравнения имат форма, подобна на параметричното уравнение за права линия в пространството. Този тип често се използва при конвертиране на векторно уравнение в едно общо за равнина.
Паралелни равнини
Има само две възможности за относителното положение на двете равнини в пространството. В този раздел на статията даваме условие, когато те са успоредни.
Ако две уравнения на равнината са дадени в обща форма, тогава техният паралелизъм е съвсем прост. Две равнини ще бъдат успоредни, ако техните вектори са такива. Да предположим, че има две уравнения:
A 1 * x + B 1 * y + C 1 * z + D 1 = 0;
A 2 * x + B 2 * y + C 2 * z + D 2 = 0.
Перпендикулярно на всяка от равнините на вектора са координатите:
п1 (А1; В1; С1);
n 2 ¯ (A 2 ; B 2 ; C 2 ).
Ако векторът n 1 ¯ може да бъде представен като умножение с реално число на вектора n 2 ¯, тогава и двете ще бъдат паралелни, т.е.
n 2 ¯ = l * n 1 ¯, където l е реално число.
Друг начин за определяне на техния паралелизъм е да се намери косинусът на ъгъла между тях чрез скаларния продукт и модулите на векторите. Този косинус трябва да е равен на единица, след това векторите (равнините) ще бъдат успоредни. Съответната формула е:
cos (=) = | (n 1 ¯ * n 2 ¯) | / (| n 1 ¯ | * | n 2 ¯ |) = 1.
Ако уравненията на равнините са дадени в параметрична векторна форма, тогава паралелизмът в пространството на равнините също се определя от условието за паралелизъм на нормалите към тях. За да се намерят векторите на посоката на тези нормали, трябва да се вземат векторните продукти на векторите, формиращи всяка равнина.
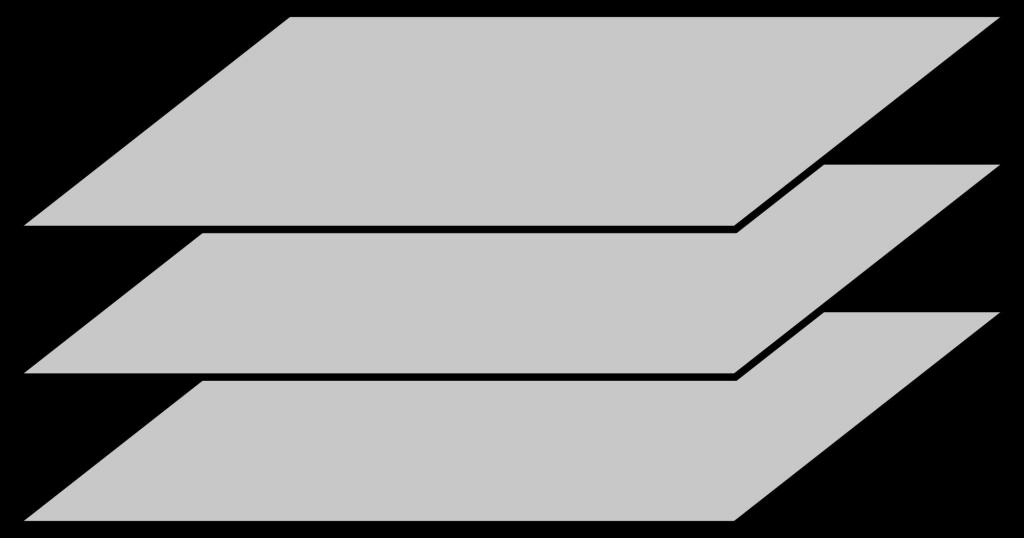
Фигурата по-горе показва три равнини, които са успоредни една на друга.
Пресичане на равнини
Това е втората версия на взаимното подреждане в пространството на равнините. В този случай двете равнини се пресичат по права линия, която им принадлежи. В този случай е важно да може да се изчисли диедричният ъгъл на това пресичане. Той винаги е равен на ъгъла между съответните водещи вектори, т.е. между перпендикулярите на равнините.
В предишния параграф вече е дадена формула, която позволява да се изчисли ъгълът между нормалите. Тук ще го отворим само като напишем координатите на векторите n 1 ¯ и n 2 ¯:
ar = arccos (| A 1 * A 2 + B 1 * B 2 + C 1 * C 2 | / (2 (A 1 2 + B 1 2 + C 1 2 ) * √ (A 2 2 + B 2 2 + C 2 2 ))).
Тази формула често се използва при изчисляване на диедричните ъгли между равнините на пирамида или наклонена призма.
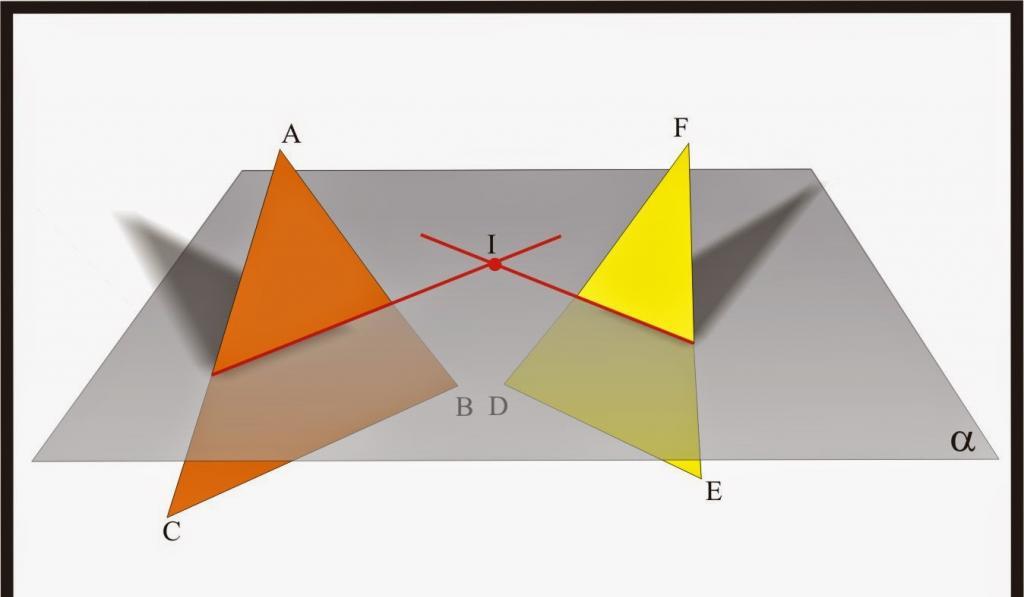
Две равнини, които пресичат третата хоризонтала, са показани на фигурата по-горе.
Конкретен случай на пресичане на две равнини е ъгълът φ = 90 o , т.е. има перпендикулярност на разглежданите геометрични обекти. За да се определи перпендикулярността, не е необходимо да се изчислява ъгълът φ, използвайки донякъде тромавата формула по-горе, за което е достатъчно да се изчисли стойността на скаларния продукт n 1 ¯ и n 2 ¯. За перпендикулярни равнини е нула, т.е.
(n 1 ¯ * n 2 ¯) = A 1 * A 2 + B 1 * B 2 + C 1 * C 2 = 0.
Пакет от самолети
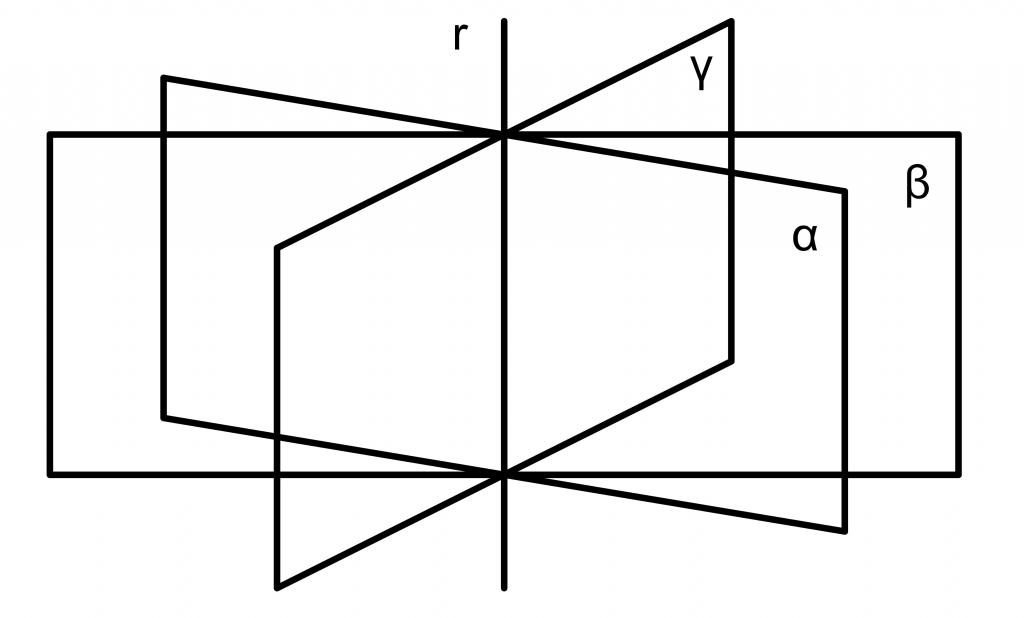
Ако две равнини се пресичат, всичките им общи точки лежат на една права линия. Забележете, че един от методите за задаване на права линия в пространството е система от две общи уравнения на равнината. Колко равнини в пространството могат да бъдат изтеглени през една права линия? Безкраен брой. Тяхното събиране се нарича пакет. Уравнението, което описва този пакет, има следната форма:
k 1 * (A 1 * x + B 1 * y + C 1 * z + D 1 ) + k 2 * (A 2 * x + B 2 * y + C 2 * z + D 2 ) = 0.
Тук k 1 и k 2 са произволни числа. Специален случай е ситуацията, когато един или и двата параметъра k не могат да приемат стойността нула. Да предположим, че k 1 ≠ 0, тогава уравнението на лъча може да бъде пренаписано във формата:
(A 1 * x + B 1 * y + C 1 * z + D 1 ) + k 2 / k 1 * (A 2 * x + B 2 * y + C 2 * z + D 2 ) = 0.
Това равенство описва всички равнини на лъча, с изключение на един с директен вектор n 2 ¯ (A 2 ; B 2 ; C 2 ).
Пример за пакет от самолети е сбор от листове от отворена книга.

След това решаваме няколко геометрични задачи, като прилагаме получените знания за свойствата на равнините в пространството.
Конвертирайте параметричното векторно уравнение към общото
Като се има следното равнинно уравнение в параметричната векторна форма:
(x; y; z) = (1; 2; 0) + α * (1; 2; 3) + β * (- 1; 3; 0).
Необходимо е да го напишем като общо уравнение на равнината в пространството.
Нека го пренапишем изрично:
x = 1 + α - β;
у = 2 + 2 * a + 3 * р;
z = 3 * a.
От последния израз получаваме α, след това го заместваме в първото равенство и изразяваме β. Намерените параметри се заменят във второто уравнение, имаме:
α = z / 3;
β = 1 - x + z / 3;
y = 2 + 2 * z / 3 + 3 - 3 * x + z =>
y + 3 * x + 5/3 * z - 5 = 0 =>
9 * x + 3 * y + 5 * z -15 = 0.
По този начин, за да се получи общо уравнение от параметричен вектор, трябва първо да го напишем изрично и след това да изразим параметрите по отношение на променливите координати.
Преобразуване на общо в параметрично векторно уравнение
Тази задача е напълно противоположна на предишната. Помислете за техниките за решаването му.
Като се има предвид следното уравнение:
x-2 * y + 3 * z -1 = 0.
Първо, една координата трябва да бъде изразена на две. Експресно, например x:
x = 2 * y-3 * z +1.
Това означава, че всяка точка с координати ще принадлежи на равнината:
(2 * y-3 * z +1; y; z).
Сега ще пренапишем тази координата като сумата от три вектора, първата ще съдържа само променливата y, втората - само z, а третата ще се състои само от числа. Имаме:
(x; y; z) = (2 * y; y; 0) + (-3 * z; 0; z) + (1; 0; 0).
Вижда се, че отваряйки това уравнение, получаваме общите координати на точка от равнината. Сега остава само да изчислим променливите в първия и втория вектори и да ги предефинираме с параметрите α и β. Получаваме:
(x; y; z) = (1; 0; 0) + α * (2; 1; 0) + β * (- 3; 0; 1).
Получихме уравнение в параметрична векторна форма, подобна на оригиналната.
Изображение на равнината в координатната система
Задачата е следната: според известното уравнение трябва да се начертае равнина в пространството. Съответното уравнение е:
3 * x - y -4 * z +5 = 0.
За да се изобрази тази равнина, е необходимо да се намерят точките, в които тя пресича координатните оси. За да направите това, можете да получите съответното уравнение в сегментите. Обаче в този случай ще продължим по различен начин: поставяме две координати, равни на нула и изчисляваме третата. Имаме:
у = 0; z = 0; х = -5/3;
х = 0; z = 0; у = 5;
х = 0; у = 0; z = 5/4.
Остава да поставите получените точки по координатните оси и да начертаете равнина през тях. Положението на равнината в пространството е показано на фигурата по-долу.
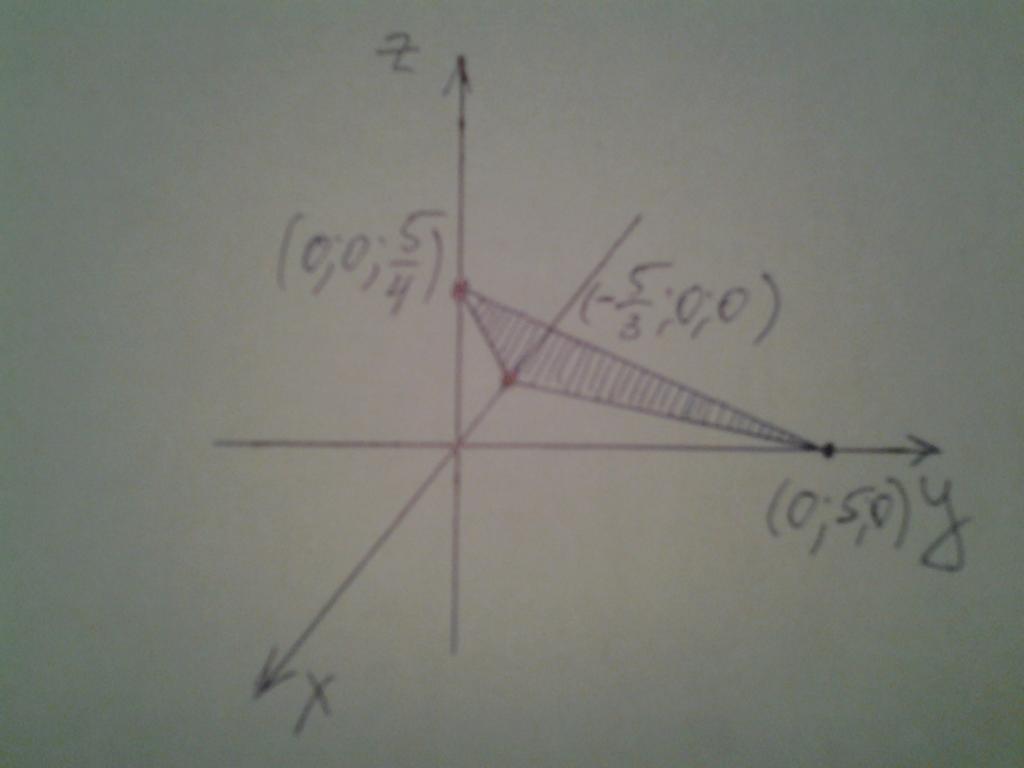
Три точки и равнина
Нека се дадат три точки в пространството:
М (1; -1; 3);
N (3; 2; -4);
L (2; 5; 0).
Необходимо е да се намери равнината, която минава през тях.
Известно е от геометрията, че три точки, които не лежат на една права линия, определят еднозначно равнината. Неговото уравнение може да бъде съставено, ако намерим неговия вектор, водещ п ¯. Тя ще бъде равна на векторния продукт на копланарните вектори, разположени в равнината. Координатите на векторите могат да се получат от координатите на точките, например:
MN¯ (2; 3; -7);
ML¯ (1; 6; -3).
Техният векторен продукт ще даде вектора n¯. Изчислявайки го, получаваме:
n¯ (33; -1; 9).
Като вземем за пример точката М, получаваме общото уравнение във вид:
33 * x -y + 9 * z - 61 = 0.
Можете да замените координатите на точките N и L с уравнението и да се уверите, че равенството е валидно.