Френелова дифракция на кръгъл отвор и диск

Дифракция на светлината проявява се в светлинната вълна, огъваща се около малки препятствия, докато се наблюдават отклонения от законите на геометричната оптика. Това се отнася и за светлинните вълни, преминаващи през отвор, например в обектива на камерата или през зеницата на окото. Има дифракция на Френел и Фраунхофер. Разликите се състоят в големината на разстоянието между източника на светлина, препятствието и екрана, на който се наблюдава картината на това явление.

Място на дифракция в общата серия от оптични явления

Преминаването на светлина (и общо взето електромагнитни вълни чрез различни нехомогенни среди е придружено от явления на тяхното отражение, дифракция и пречупване. Когато вълната достигне границата на две медии, тя се разделя на отразена, която остава в оригиналната среда, но с промяна на посоката на разпространение и пречупване, която минава през границата на медията, но също и с промяна на посоката. Дифракцията на Френел е процес на промяна в посоката на светлинната вълна, когато тя не се сблъсква с границите на две среди, а с някакво непрозрачно препятствие с дупка (или без нея, но малки размери) в същата среда. Степента на дифракция нараства с увеличаване на дължината на светлинната вълна.

Феноменът на откритието

Вероятно първият, който наблюдава дифракцията е Франческо Мария Грималди (2 април 1618 - 28 декември 1663 г.), италиански йезуитски свещеник и в същото време математик и физик, преподавал в йезуитския колеж в Болоня. Втората половина от живота си посвещава на изучаването на астрономия и оптика.

Грималди е известен с работата си, озаглавена "Физическата наука за светлината, цветята и дъгите", публикувана в Болоня през 1665 година. Повечето от тях се състоят от досадно обсъждане на природата на светлината от теологична гледна точка и не е от интерес днес. В допълнение, книгата съдържа и сведения за множество експерименти, свързани с дифракцията на светлинните лъчи.

Базирайки се на ежедневния опит, хората от древни времена заключават, че лъчите на светлината се разпространяват по прави линии. В края на краищата, обект, който е между, например, пламък на свещ и стена, хвърля сянка с остра граница, сякаш директните лъчи на светлината се разбиват на непрозрачна бариера.

Въпреки това, резултатите от експериментите на Грималди противоречат на тези идеи, които бяха установени в продължение на хиляди години. Оказва се, че ако осветявате различни обекти през препятствие с малка дупка, тогава сенките от тях няма да бъдат същите като при липса на препятствие. Оказа се, че светлината може да промени посоката на разпространение и да заобиколи малки препятствия.

Как се открива дифракцията на Френел в кръгъл отвор

Грималди, прехвърляйки светлината на слънцето в тъмна стая през малка дупка (отвор), забеляза, че ширината на сянката на тънки предмети като игли и коса на екрана е много по-голяма (както се вижда на снимката по-долу), отколкото ако светлинните лъчи минават прави линии.

Той също така отбеляза, че кръгът на светлината, образуван на екрана от лъчи, преминаващи през много малка дупка в олововата плоча, е значително по-голям, отколкото би било, ако тези лъчи паднат направо на екрана. Грималди заключи, че те променят посоката си, когато минават покрай ръбовете на дупката.

В неговите експерименти, провеждани в една и съща стая, светлината, в която преминава през дупките в жалузите, разстоянието между препятствието за светлинни вълни (плоча с кръгла дупка) и екранът е малък. Дифракцията на Френел също отговаря на тези условия. Анализирайки го, не можем да пренебрегнем кривината на фронта като първоначална вълна на препятствие и вторични вълни. Те придават на екрана дифракционно изображение на препятствие с дупка, както е показано на снимката по-долу.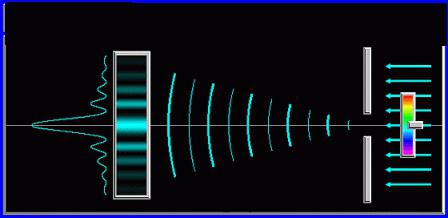

Какво се случва, ако светлината пада върху малка непрозрачна пречка

Грималди открил също, че сянката на малко тяло (с неправилна форма) е заобиколена от три цветни ивици или ленти, които се стесняват, когато се отдалечават от центъра на сянката. Ако първоначалният светлинен поток беше по-силен, той възпроизвежда подобни цветни ленти в самата област на сянката: имаше две или повече такива ленти и броят им нарастваше пропорционално на разстоянието между сянката и осветеното тяло.

И в този случай, Grimaldi е в състояние да наблюдава феномена, който по-късно е наречен "Френелова дифракция", в резултат на което на екрана е получена дифракционна картина на препятствието. Аналитично изчисляване е много трудно. Съществуват обаче методи, които позволяват в някои конкретни случаи значително да се опрости това изчисление.

И още една забележка за експериментите на Грималди. Ако е използвал кръгъл диск (например чинийка) като екран в тях, тогава може би щеше да може да наблюдава такова нещо като дифракцията на Френел на кръгъл диск един век и половина по-рано, отколкото се е случило. Но историята като цяло и историята на науката в частност не знаят. подчинително. Следователно, този експеримент е проведен едва в началото на 19 век. (виж по-долу).

Първо наблюдение на смущения

прескочи слънчеви лъчи в стаята през няколко малки кръгли дупки, Грималди получил следи от припокриващи се конуси на светлината на екрана. Както можеше да се очаква, в райони, където падаха лъчи от две дупки, екранът светеше повече, отколкото би било от един конус на светлина; но изследователят беше изненадан да открие, че онези части от общата сянка, в които конусите на светлината се наслагват един върху друг, се оказаха по-тъмни от съответните части, в които нямаше наслагване (фигура по-долу). 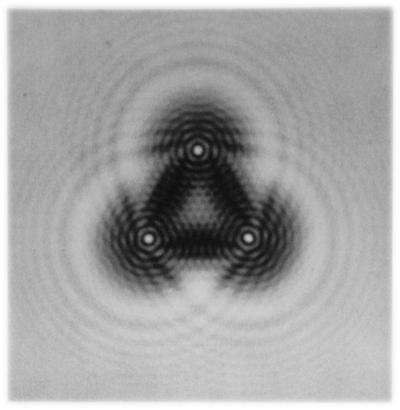Така за първи път беше записано, че осветеното тяло може да стане по-тъмно, ако добавим светлина към това, което вече получава. Сега знаем, че причината за това е интерференция, т.е. взаимно усилване или намаляване на светлинните вълни. Той се проявява и в такова явление като дифракцията на Френел. Много съвременни учени дори не правят фундаментално разграничение между тези понятия, като намаляват всички дифракционни прояви до прояви на интерференция, както направи, например, Р. Фейнман в 3-ти том на неговите “Feynman Lectures on Physics”.

От Грималди до Хюйгенс и Нютон

Първият опит да се обясни причината за отклонението на светлината от прямолинейното разпространение е направен от известния английски учен Р. Гук. Той предположи, че светлината е вълновата осцилация на световния етер, който след това се разбира като всепроникващото вещество, което изпълва цялото пространство. Идеята на Хук вече е поставила основата за бъдещо правилно обяснение на това какво са дифракцията на Френел и всички оптични явления. Той обаче не успя да създаде подходяща количествена теория.

Следващата стъпка е направена от Кристиан Хюйс, който формулира известния си принцип през 1690 г. Според него видимата светлина е колекция от сферични вълни, разпространяващи се от източника във всички посоки в етера. В този случай източникът на тези вълни може да бъде не само етерни частици, възбудени директно от светлинен източник (например пламък на свещ), но също и всички други негови частици в точките в пространството, които светлината преминава по време на разпространението. Получената видима вълна е във всеки момент като обвивка на всички вторични вълни. Последното може да се разпространи извън границите на препятствията по пътя на светлината, което е добре насложено върху картините на техните сенки, наблюдавани по време на дифракцията. Ето защо, според тази теория, няма просто препятствие около светлината - от новите (вторични) източници, които се простират отвъд пречките.

Въпреки това, според принципа на Хюйгенс, тесните светлинни лъчи са невъзможни - ръбовете им трябва незабавно да се разпространят във всички посоки. Въпреки това, те могат да се видят с просто око, както е било в експериментите на Грималди. Налице е противоречие между теорията и практиката.

И. Нютон се опитва да я преодолее в своята корпускуларна теория на светлината, която също дава обяснения за всички оптични явления, включително и за дифракцията на светлината на Френел. Въпреки това, основният постулат на Нютон, че светлината не е вълна във въздуха, а поток от тела (корпускули), поражда други противоречия. Така че, не е ясно защо пресичащите се светлинни лъчи не засягат помежду си, тъй като корпускулите трябва да се сблъскат един с друг. Но авторитетът на Нютон беше толкова висок, че вълновата теория за светлината беше забравена за повече от сто години.

Светлинните вълни се връщат

През 1880 г. английският физик Т. Юнг предложил да се върне към вълновата теория на светлината, допълнена от концепцията за интерференция на светлинните вълни. Това означава, че когато кохерентните (с еднакви честоти) вълни се припокриват, интензивността на светлинния интензитет в някои точки на полето и затихването при други в зависимост от фазовото съотношение на добавените светлинни вълни е стабилна.

Концепцията за намеса е използвана от френския физик О. Френел, за да ги допълни с принципа на Хюйгенс. Според неговия вариант всички вторични сферични вълни са кохерентни и пречат на налагането. Какъв е физическият механизъм на дифракцията на Huygens-Fresnel?

Преминава светлината през кръглия отвор

Когато светлинната вълна се разпространява през дупка, връзката между нейния диаметър и дължината на вълната на падащия лъч определя поведението на светлината. Както е показано от лявата страна на фигурата по-долу, когато дължината на вълната е значително по-малка от диаметъра на отвора, тя просто преминава напред по права линия, сякаш изобщо няма пречки.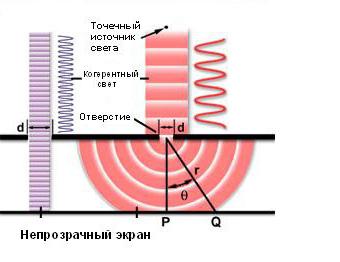

От дясната страна на фигурата обаче е показана различна ситуация. В този случай дължината на вълната на светлината, предавана от точков източник, надвишава диаметъра на отвора, а дифракцията на Френел възниква на апертурата. При анализа на това явление дупката се счита за отсъстваща и вместо нея се поставя набор от фиктивни вторични източници на светлина, които възбуждат същите вторични сферични вълни, които вече са споменати по-горе. Те се разпространяват по посока на екрана и достигат до различни точки с различни фази, като се намесват един с друг, т.е. увеличават или отслабват във всяка такава точка. Защото цялата система има аксиална симетрия, тогава падащият цилиндричен лъч на светлината се превръща в коничен, а на екрана има също така и осесиметрична дифракционна картина на редуващи се светли и тъмни пръстени, наричани съответно максимуми и минимуми на осветяване. В точка P, разположена върху оста на дупката, ще има светло петно ​​- основният максимум, а първият от вторичните максимуми на осветление ще се появи в точка Q. Интензивността на вторичните максимуми намалява с увеличаването на разстоянието им от центъра на дифракционния модел. Съотношението между размера на отвора и степента на дифракция се определя от следното уравнение:

sinθ = λ / d, където

• θ е ъгълът между посоката на центъра на дифракционната картина и посоката на първия минимум,
• λ е дължината на светлинната вълна.

Фигурата по-долу показва как интензивността на осветеността на екрана варира в зависимост от ъгловото разстояние от центъра. Отбележете, че минимумите между вторичните максимуми са разположени в точки, кратни на.

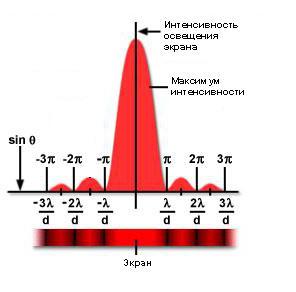
Аналитичното изчисляване на картината на такова явление като дифракция на Френел върху дупка и диск е значително опростено поради аксиалната симетрия, което ще бъде разгледано по-долу.

Кръгъл диск по пътя на лъч светлина

Ако следваме теорията на Френел, тогава, когато кръгъл непрозрачен диск се постави върху лъч светлина, всички точки по ръбовете му стават източници на кохерентни вторични сферични вълни. Разстоянията между тези точки и точката на пресичане на оста на диска с непрозрачен екран перпендикулярно на нея са едни и същи. Следователно вълните от всички точки на ръба на диска трябва да се пресичат по едно и също време и в една и съща фаза, т.е. те трябва да бъдат сгънати и значително да се укрепват взаимно. Оказва се, че в центъра на кръговата сянка от диска трябва да се наблюдава светло осветено петно, както е показано на фигурата по-долу. 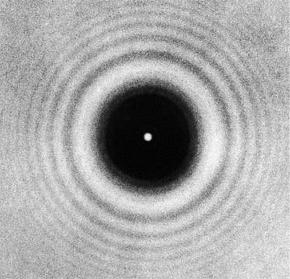Това обстоятелство за първи път е забелязано от френския физик С. Поасон, който е бил противник на теорията на Френел. Той счита, че отбелязаното от него обстоятелство доказва неговата непоследователност. Каква беше изненадата му, когато Френел заедно с Араго направи съответния опит и получи такова място в центъра на сянката от диска! Фигурата по-долу показва схематично този опит.

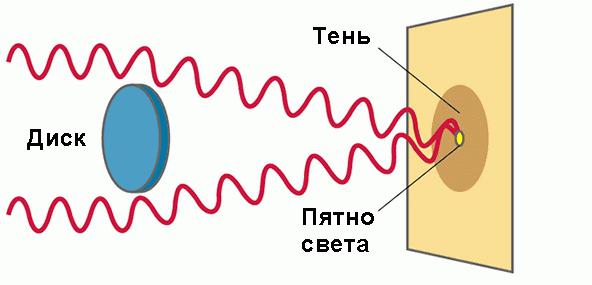
Така дифракцията на Френел се проявява на диска. Яркото петно ​​в центъра на сянката получи името на точката на Поасон. Ако дискът е малък, тогава интензитетът на светлината в центъра на неговото дифракционно изображение е почти същият, както при неговото (дисково) отсъствие.

Как да изчислим дифракционни модели

В общия случай, изчисляването на интерференцията на вторичните вълни за получаване на дифракционна картина е трудно. Но при асиметричните случаи тя може да бъде опростена, така че цялата картина на явлението дифракция да стане проста. Методът на Френеловите зони ви позволява да визуално геометрично да пречупвате предната част на сферичната вълна в кръгови участъци.

Амплитудите и относителните фази на всички зони се вземат предвид при изчисляване на разпределението на интензитета. Така се използва доста сложна математическа обработка, за да се определи дифракционната картина. Но когато се анализира такова явление като дифракция на Френел на кръгъл отвор и диск, тя е значително опростена.

На фигурата по-долу S е точков източник на светлина. 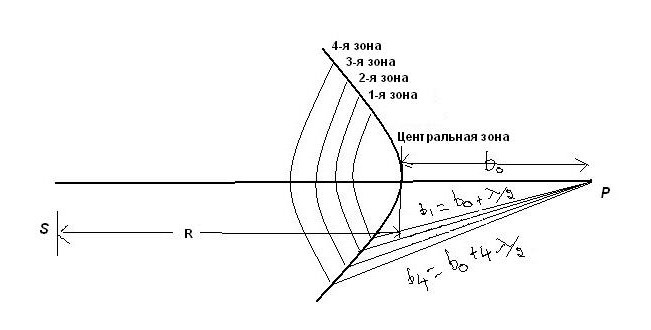S излъчва сферична светлинна вълна с дължина λ в посока от ляво на дясно. Нека радиусът на фронта му при време t е равен на R. Ефектът на този фронт на вълната в точка P се определя чрез разделянето му на пръстеновидни зони. Разстоянията от краищата на две последователни зони до точка Р се различават с λ / 2. Зоните на звънене с това свойство се наричат ​​зони на Френел. Разстоянието от нулевата зона до точката P е b ₀ .

Първата зона е на разстояние b ₁ = b ₀ + λ / 2; второто: b ₂ = b ₀ + 2λ / 2; трето: b ₃ = b ₀ + 3λ / 2; i-та зона: b _i = b ₀ + iλ / 2.

Последователните ръбове на две съседни зони са разположени в подобни точки. Ако в тях се възбуждат вторични сферични вълни, те идват в точката на наблюдение Р с фазова разлика от 180 ° и взаимно отслабват взаимно, когато се наслагват (но не се разрушават).

Дифракция на Френел върху кръгъл отвор и диск - картина с аксиална симетрия. Следователно, прилагането на този метод позволява значително опростяване на конструкцията на дифракционен модел, когато светлината преминава през такива препятствия.

Как зоните на Френеловия пръстен работят на кръгла дупка?

Обмислете отново случая, когато дифракцията на светлината се появява на кръгла дупка. Зоните на Френел, в които фронтът на вълната може да бъде счупен, поставен в отвора на даден диаметър на определена дължина на вълната λ и разстоянието отпред до екрана b ₀ , може да бъде в количество, изразено с нечетно или четно число. Както е отбелязано по-горе, вторичните вълни от две съседни зони във всяка точка на екрана отслабват, въпреки че не се разрушават взаимно. Следователно, ако за центъра на дифракционната картина броят на френеловите зони, които се вписват в дупката, е нечетен (2k + 1), то амплитудата на осветяването в центъра на картината ще бъде сумата от остатъка от първата (централна) зона и некомпенсираното действие (2k + 1) - зони, които се подсилват взаимно. Дифракционният модел за този случай е показан на фигурата по-долу.

Ако броят на зоните на Френел, натрупани в дупката, е равен, тогава влиянието на всички зони в центъра на картината ще бъде взаимно компенсирано по двойки и в него ще се появи тъмно петно.