Последователността на Фибоначи и принципите на Златния раздел

Последователността на Фибоначи, която стана известна на мнозинството чрез филма и книгата Da Vinci Code, е поредица от числа, получени от италианския математик Леонардо от Пиза, по-известен с псевдонима Фибоначи, през тринадесети век. Последователите на учения забелязват, че формулата, в която тази поредица от числа е подчинена, намира отражението си в света около нас и резонира с други математически открития, като по този начин ни отваря вратата към тайните на Вселената. В тази статия ще опишем какво е последователността на Фибоначи, разгледаме примери за картографиране на този модел в природата и го сравним с други математически теории.

Формулиране и определение

Серията на Фибоначи е математическа последователност, всеки елемент от която е равна на сумата от предишните две. Нека някой член на последователността е _xn. Така се получава формула, която е валидна за цялата серия: _{xn + 2} = _xn + _{xn + 1.} С това последователност ще изглежда така: 1, 1, 2, 3, 5, 8, 13, 21, 34. Следващото число ще бъде 55, тъй като сумата от 21 и 34 е 55. И така нататък по същия принцип.

Примери в околната среда

Ако погледнем към растението, по-специално върху короната на листата, ще отбележим, че те цъфтят по спирала. Ъглите се формират между съседни листа, които от своя страна образуват правилната математическа последователност на Фибоначи. Благодарение на тази функция всеки лист, който расте върху дърво, получава максимално количество слънчева светлина и топлина.

Математически пъзел на Фибоначи

Известният математик представя своята теория като загадка. Звучи по следния начин. Можете да поставите чифт зайци в затворено пространство, за да разберете колко двойки зайци ще бъдат родени в рамките на една година. Като се има предвид естеството на тези животни, фактът, че всеки месец един чифт е способен да произведе нов чифт, и те са готови да се размножават след достигане на два месеца, в крайна сметка той получи известния си брой номера: 1, 1, 2, 3, 5, 8 , 13, 21, 34, 55, 89, 144 - където е показан броят на новите двойки зайци на всеки месец.

Последователност на Фибоначи и пропорционално съотношение

Тази серия има няколко математически нюанса, които определено трябва да разгледате. Той, приближавайки се по-бавно и по-бавно (асимптотично), се стреми към някакво пропорционално съотношение. Но това е ирационално. С други думи, това е число с непредсказуема и безкрайна последователност от десетични числа в дробната част. Например, съотношението на всеки елемент от поредицата варира около числото 1.618, след което надминава, след което достига. Следното по аналогия приближава 0.618. Какво е обратно пропорционално на броя 1.618. Ако разделим елементите през един, ще получим 2.618 и 0.382. Както вече разбрахте, те също са обратно пропорционални. Получените числа се наричат ​​коефициенти на Фибоначи. Сега ще обясним защо извършихме тези изчисления.

Златно съотношение

Разграничаваме всички обекти около нас според определени критерии. Една от тях е форма. Някои от нас привличат повече, други по-малко, а някои не харесват. Забелязва се, че симетричен и пропорционален обект е много по-лесно възприеман от човека и предизвиква усещане за хармония и красота. Цялото изображение винаги включва части с различни размери, които са в определено съотношение един с друг. Оттук и отговорът на въпроса за това, което се нарича Златна секция. Това понятие означава съвършенството на връзката между цялото и частите в природата, наука, изкуство От математическа гледна точка, разгледайте следния пример. Вземете сегмент от всяка дължина и го разделете на две части, така че по-малката част да се отнася до по-голямата като сума (дължината на целия сегмент) към по-голямата. Така че, използваме сегмента c за стойността на единица. Нейната част а ще бъде равна на 0.618, а втората част б , се оказва, е равна на 0.382. По този начин ние се съобразяваме със състоянието на Златния раздел. Съотношението на сегмент c към a е равно на 1,618. А съотношението на части c и b е 2,618. Получаваме вече познатите ни коефициенти на Фибоначи. По същия принцип са изградени златен триъгълник, златен правоъгълник и златен кубоид. Заслужава да се отбележи също, че пропорционалното съотношение на частите на човешкото тяло е близко до Златното съотношение.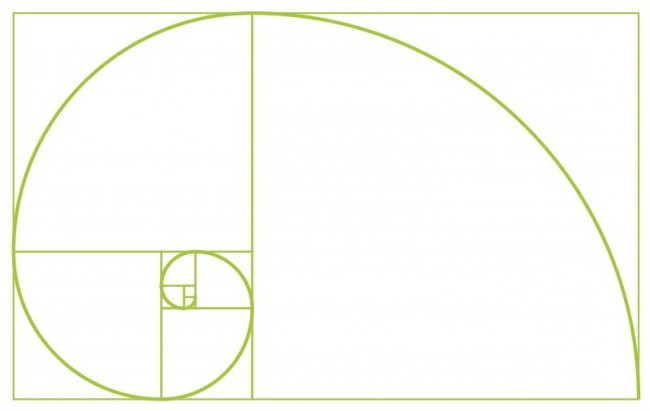

Последователността на Фибоначи е основа на всичко?

Нека се опитаме да комбинираме теорията на Златната секция и известната серия от италиански математици. Да започнем с два квадрата от първия размер. След това отгоре добавяме друг квадрат от втория размер. Нека рисуваме до същата фигура с дължината на страната равна на сумата от двете предни страни. По същия начин начертайте квадрат от петия размер. И така можете да продължите за неопределено време, докато не ви омръзне. Главното е, че размерът на страната на всеки следващ квадрат е равен на сумата от стойностите на страните на предишните две. Получаваме серия от полигони, чиято дължина е Числата на Фибоначи. Тези цифри се наричат ​​правоъгълници на Фибоначи. Нека нарисуваме гладка линия през ъглите на нашите полигони и да получим ... една спирала на Архимед! Увеличаването на височината на тази цифра, както знаете, винаги е еднакво. Ако включите фантазията, тогава получената картина може да бъде свързана с черупката на мида. От това можем да заключим, че последователността на Фибоначи е в основата на пропорционални, хармонични съотношения на елементи в заобикалящия ни свят.

Математическа последователност и вселена

Ако се вгледате внимателно, тогава Архимедова спирала (някъде изрично, но някъде забулена) и следователно принципът на Фибоначи може да бъде проследена в много от обичайните природни елементи, които обграждат човек. Например, една и съща мида черупки, броколи цветове, слънчогледово цвете, конус иглолистни растения и други подобни. Ако погледнем встрани, ще видим последователността на Фибоначи в безкрайните галактики. Дори човек, вдъхновен от природата и възприемащ формата си, създава обекти, в които е проследена гореспоменатата серия. Сега е моментът да си припомним Златната секция. Наред с модела на Фибоначи, принципите на тази теория се проследяват. Има версия, че последователността на Фибоначи е вид тест на природата, който да се адаптира към по-съвършена и фундаментална логаритмична последователност на Златната секция, която е почти идентична, но няма начало и е безкрайна. Природата на природата е такава, че трябва да има своя собствена отправна точка, от която да се гради, за да създаде нещо ново. Връзката на първите елементи от сериите на Фибоначи е далеч от принципите на Златния раздел. Но колкото по-нататък продължаваме, толкова повече се изглажда това несъответствие. За да се определи последователността, е необходимо да се познават нейните три елемента, които следват един след друг. За Златната последователност двама са достатъчни. Тъй като е и двете аритметични и геометрична прогресия.

заключение

И все пак, въз основа на горното, можете да зададете доста логични въпроси: "Откъде идват тези числа? Кой е авторът на целия свят, който се е опитал да го направи перфектен? Всичко винаги ли е било така, както той искал? Ако е така, защо не успя?" Какво ще се случи след това? Намирайки отговора на един въпрос, получавате следващия. Реших го - още два. След като ги разрешите, получавате още три. След като се справите с тях, ще получите пет нерешени. Тогава осем, след това тринадесет, двадесет и един, тридесет и четири, петдесет и пет ...