Динамика и кинематика на кръговото движение: формули и решение на типичен проблем

Възможността да се опише движението в кръг е важна за изчисляване на техническите характеристики на въртящите се валове и зъбни колела. Този вид движение се среща и в ежедневието и природата, като ротация на планетите около слънцето и скейтъри по време на изпълнения на спортни състезания. В тази статия ще разгледаме как от гледна точка на физиката може да се опише този вид движение.

Динамика на ротация

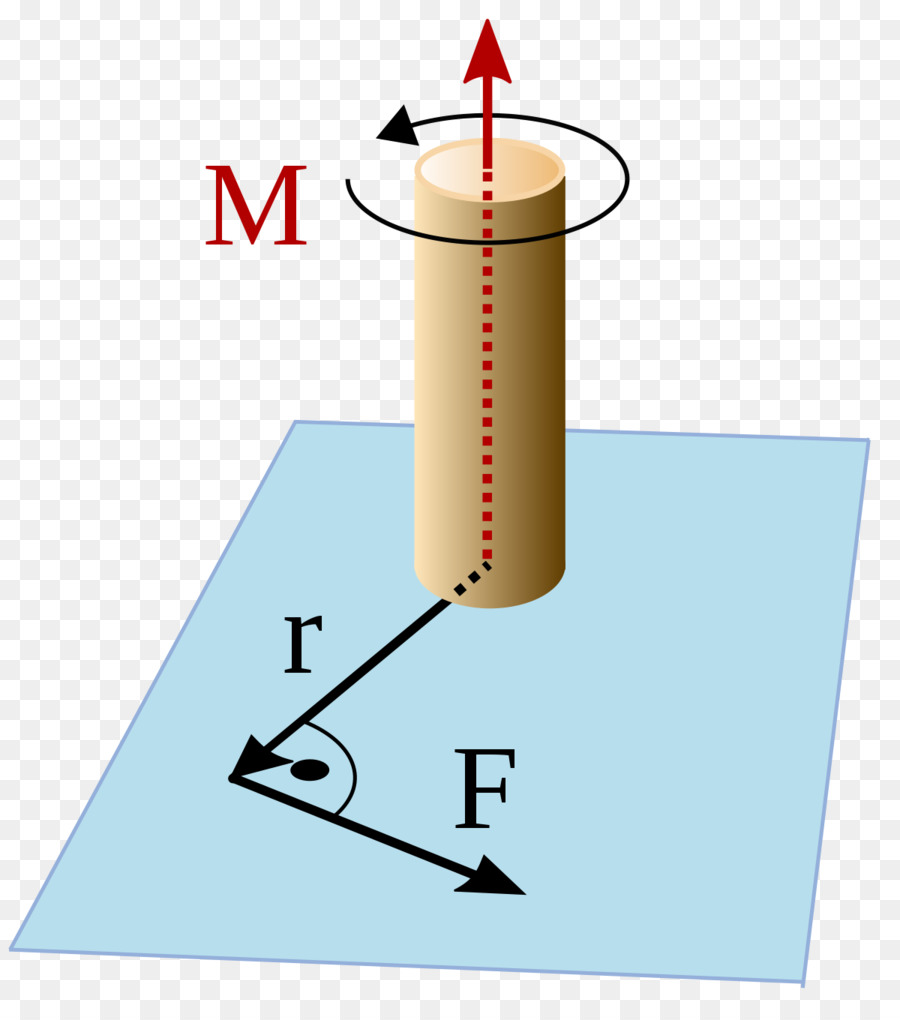
Движението в кръг е въртенето на определено тяло или материална точка около ос. За да започне тялото да се върти, е необходимо да има външен въртящ момент, действащ върху въпросната система. Този момент се определя по формулата:

M = F * d

Тук F е силата, d е дължината на лоста (разстоянието между оста и точката на прилагане на силата). Моментът на сила е векторна стойност. Формулата се използва за изчисляване на модула М.

Ефектът на момент М се отразява върху системата под формата на появата на ъглово ускорение. Това означава, че системата започва да се върти. Основната формула за кръговото движение е:

M = I * a

Тук I е моментът на инерцията, α е ъгловото ускорение. И двете величини имат аналози за линейния случай. Ако всичко е ясно с аналога на стойността на α, то за момента на инерцията трябва да се изясни. Стойността на I отразява инерционните свойства на въртящата се система. Това означава, че по време на въртене, той играе същата роля като обикновеното телесно тегло.

Забележете, че горното изражение е аналог на втория закон на Нютон за ротация.

Центростремителни и центробежни сили, ускорение

Процесът на въртене предполага наличието на някаква вътрешна сила, която би осигурила криволинейното движение на тялото. Тази сила се нарича центростремителна. Според името, тя винаги е насочена от тялото към оста на въртене. Тъй като дължината на лоста d за него е нула, това не води до появата на ъглово ускорение α. Въпреки това той променя линейния вектор на скоростта, т.е. създава ускорение.

Ускорението при движение в кръг без промяна на модула на линейната скорост се нарича центростремително. Изчислява се по формулата:

a _c = v2 / r

Където v е линейната скорост на материалната точка, която се върти на разстояние r от оста.

В допълнение към центростремителната често можете да чуете за центробежната сила. Последният се стреми да извади тялото от кръгова пътека към права линия. Причината за неговото възникване са инерционните свойства на въртящата се система.

Когато се движат в кръг, центростремителните и центробежните сили са еднакви по величина, а в посоката, в която са противоположни.

Кинематични уравнения на въртенето

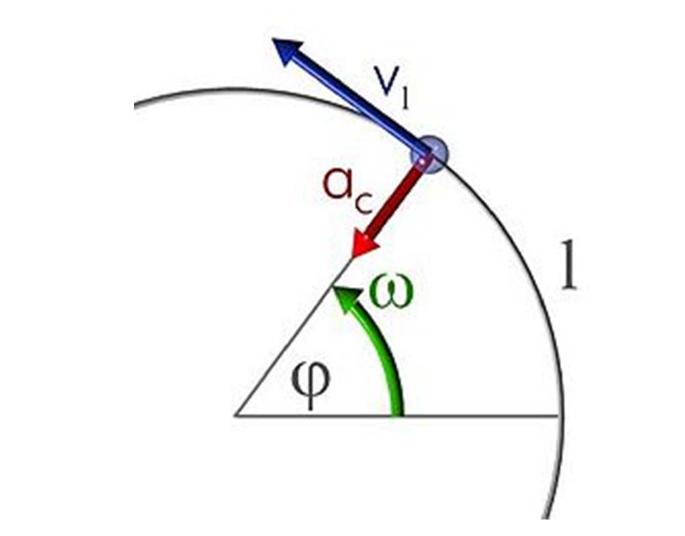
Движението в кръг, както в права линия, може да бъде еднородно или да се случи с ускорение. В първия случай формулата е:

θ = ω * t

Тоест, централният ъгъл θ, върху който тялото се превръща по време t, е право пропорционален на ъгловата скорост ω. Ъгълът θ се изразява в радиани, а скоростта ω се изразява в радиани в секунда.

Ако върху системата действа постоянен външен момент на силите, то движението в кръг се осъществява с известно постоянно ускорение α. В този случай ще бъде вярно следното кинематично изражение:

θ = α * t 2/2

Ако системата първо се върти с определена скорост ω _0, а след това започва да увеличава своята честота на въртене с ускорение α, тогава, започвайки от момента на момента t, когато се появи ускорение, формулата ще бъде валидна:

θ = ω ₀ * t + α * t 2/2

Имайте предвид, че този израз е линейна комбинация от предишните две.

Връзката между линейни и ъглови кинематични характеристики

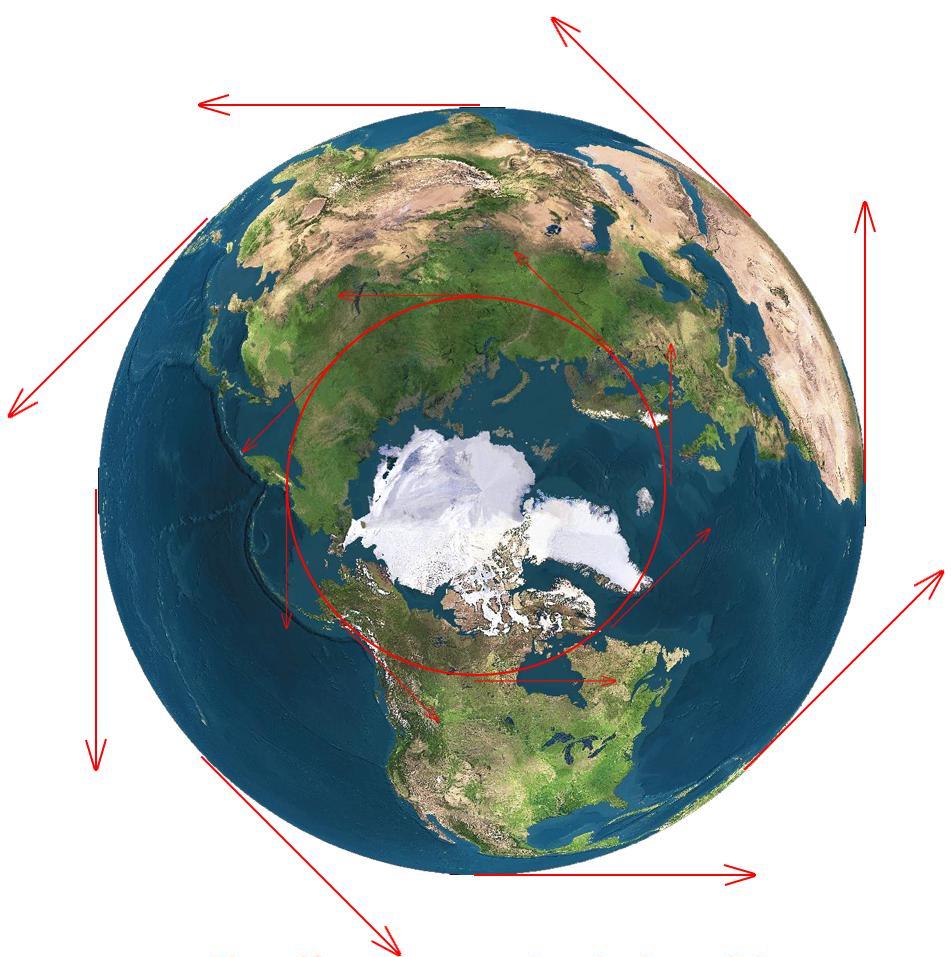
По-горе е дадена формулата за центростремителното ускорение, написана чрез линейната скорост v. Въпреки това, тази формула може да бъде записана и чрез съответните ъглови характеристики ω.

Да предположим, че въртящото се тяло прави един оборот около кръга във времето t. Тогава за линейни и ъглови скорости можем да напишем:

v = 2 * pi * r / t;

ω = 2 * pi / t

Откъдето се вижда, че модулът на линейната скорост v е r пъти по-голяма от величината на ω, т.е.

v = ω * r

Това равенство свързва ъгловите и линейните скорости. Използвайки го, можете да напишете формулата за a _c чрез ω:

a _c = ω ² * r

Сега изчисляваме във формулата със скоростите производното време за лявата и дясната страна на равенството, получаваме:

dv / dt = dω / dt * r =>

a = α * r

Това равенство свързва линейното ускорение а, насочено тангенциално към окръжността и неговия ъглов аналог α.

Лесно е да се докаже, че централният ъгъл на въртене θ при движение около окръжност е свързан с дължината на неговата дъга L, следният израз:

L = θ * r

Тук, ако θ е равен на 2 * pi радиана (пълна революция), получаваме дължината на кръга L.

Решението на проблема за определяне на центростремителната сила

Известно е, че камък с тегло 0,5 кг е свързан с въже с дължина 1 м и те започват да го въртят с ъглова честота от 3 оборота в секунда. Необходимо е да се намери силата на опън на въжето F _c .

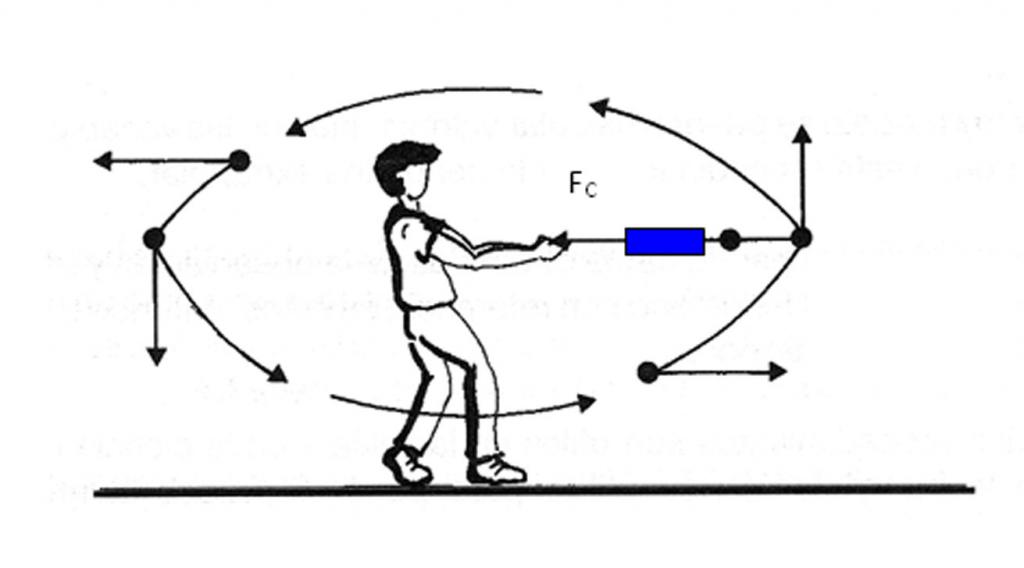
Силата на напрежение Fc е центростремителна. Може да се изчисли по формулата:

F _c = m * a _c

Масата на камъка е известна. Центростремителното ускорение a _c може да се изчисли от познаването на ъгловата скорост ω. С честотата f, зададена в задачата, количеството ω е свързано с израза:

ω = 2 * pi * f

Тогава центростремителното ускорение ще бъде изчислено като:

a _c = 4 * pi ² * f ² * r

Желаната сила Fc ще бъде равна на:

F _c = 4 * pi ² * f ² * r * m

Ако условието на задачата е да замени данните в тази формула, тогава получаваме стойността на силата F _c , приблизително равна на 177.5 N.