Принцип на Дирихле: проблеми с решения
Има много принципи в математиката. Някои от тях са доста прости и разбираеми дори за начинаещи, а някои изискват някои обяснения и доказателства. Те обаче са много ефективни и могат лесно да се прилагат на практика. Един от тях е принципът на Дирихле (известен още като принципа на гълъба / заек). Това е доста проста декларация, която може да помогне при решаването на много математически проблеми.

История на
Този принцип е формулиран от почетния немски математик Йохан Дирихле през 1834 година. Днес тя се използва както в комбинаториката, така и в математическата физика. Преведено от оригиналния немски, звучи като "принцип на кутии". Ученият проведе изследванията си със зайци и контейнери. Той показа, че ако сложим, да речем, 5 зайци в 7 контейнера, то поне в един контейнер ще има 5/7 от едно животно. Въпреки това, заекът не може да бъде разделен на части, следователно поне една клетка ще бъде празна (5/7 е 0 цели числа). По същия начин, в обратна посока, ако има 7 зайци и 5 кутии, то поне един от тях има 2 зайци (7/5 е 2 непокътнати). Започвайки от това твърдение, математиката успя да формулира принцип, който осигурява успешното решаване на проблемите в математиката в продължение на много години.
Ad
Съвременни формулировки и доказателства
Днес има няколко различни формулировки на този принцип. Най-разбираемото и просто означава, че е невъзможно да се засадят 8 зайци в 3 клетки, така че всеки да има не повече от 2. По-научна и сложна формулировка, обясняваща принципа на Дирихле, казва: ако в к-клетките има k + 1 зайци, то поне Най-малко една клетка ще съдържа повече от един заек. И ако в к-клетките има k-1 зайци, то поне 1 клетка ще съдържа по-малко от един заек. Доказателството на това твърдение е съвсем просто, така да се каже, от противоречие. Ако приемем, че във всяка клетка има по-малко зайци от k-1 / k, тогава k на зайците е по-малко от k * k-1 / k = k-1, което противоречи на началните условия.
Ad
В действителност такъв прост и разбираем принцип значително улеснява решаването на проблемите в математиката и доказването на много трудни теореми. Просто е необходимо да се има предвид, че зайците и клетките могат лесно да бъдат заменени с математически обекти и обекти (числа, точки, сегменти, фигури и т.н.).
Друга формулировка
Понякога задачите по принципа на Дирихле не са толкова прости и очевидни, както при животните в кутии. Необходимо е този принцип да се прехвърли на математически множества, за да се намерят решения. В този случай можете да разчитате на различна, по-сложна формулировка. 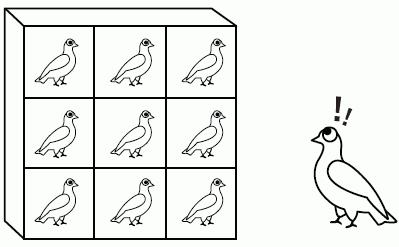
Ако съпоставим множеството S, съдържащо d + 1 елементи, към множеството R с множеството от d елементи, тогава два елемента от множеството S ще имат едно и също изображение.
Въпреки че съвременният ГЕФ в математиката налага творчески изисквания към учениците и предлага нестандартни опции, решението чрез твърдението на Дирихле не винаги е толкова просто и ясно. Понякога е много трудно да се определи коя стойност да се разглежда като животно и коя като клетка и как фактът, че има две животни в една клетка, помага за решаването на проблема. И ако успеем да го разберем, все още е невъзможно да определим в коя конкретна клетка ще бъде обектът. Тоест, можете просто да докажете съществуването на такава клетка, но не можете да я конкретизирате.
Ad
Пример номер 1. Геометрия
Съвременните примери за решаване на проблеми показват, че перфектни различни математически обекти могат да действат като животни и клетки.
задача
Линията к преминава през равнината на триъгълника ABC, но не пресича нито един от нейните върхове. Необходимо е да се докаже, че не може да прекоси трите си страни.
решение
Представете си как линията к разделя триъгълника на две равнини, да ги наречем s1 и s2. Предполагаме, че s1 и s2 са отворени, т.е. не съдържат линията k. Е, сега е моментът да приложим принципа на Дирихле. Задачите с решения могат да покажат, че в съвременните условия зайците и клетките означават различни обекти. Така че, вместо зайците, ние заместваме върховете на триъгълника, а вместо клетките - полу-равнината. Тъй като начертаната линия k не пресича нито един от върховете, всеки от тях е в една или друга равнина. Но тъй като в триъгълника има три върха и имаме само две равнини (s1 и s2), едната от тях ще съдържа два върха. Да предположим, че това са върховете А и В и те са в полу-равнината s2 (т.е. те лежат на една и съща страна на k). В този случай отсечката AB не пресича линията k. Това означава, че има страна в триъгълника, че k не се пресича.
Ad
Алтернативно решение
В този проблем предположихме, че точките А и В са в една и съща равнина, но принципът на Дирихле не посочва конкретна клетка, така че може да се отбележи, че върховете C и B, или A и C са разположени в една и съща равнина. няма значение коя страна на триъгълника се прави в права линия k. Следователно този принцип е идеален за неговото решение.
Пример № 2. Геометрия
задача
В средата на равностранен триъгълник ABC (в който AB = BC = AC = 1) се намират 5 точки. Необходимо е да се докаже, че две от тях са разположени на разстояние по-малко от 0.5.
решение
Ако начертаете средните линии в десния триъгълник на ABC, те го разделят на 4 малки правоъгълни триъгълника със страни ½ = 0.5. Да предположим, че тези триъгълници са клетки, а точките вътре в тях са зайци. Оказва се, че имаме 5 зайци и 4 клетки, затова в един от тях ще има най-малко два зайци. Като се има предвид, че точките не са върхове (тъй като те се намират в триъгълника ABC, а не на една от страните му), те ще бъдат поставени в малки фигури. Следователно разстоянието между тях ще бъде по-малко от 0,5 (тъй като размерът на сегмента вътре в триъгълника никога не надвишава размера на най-голямата му страна).
Пример номер 3. Комбинаторика
В други области принципът на Дирихле също може да бъде успешно приложен: комбинаториката и математическата физика отдавна се основават на нея при решаването на проблеми.
задача
Например, около закръглена маса, m знамена от различни страни стоят на равни разстояния един от друг, а m представители от всяка страна седят на масата, всяка от тях се намира до чуждо знаме. Необходимо е да се докаже, че с определена ротация на масата поне двама от представителите ще бъдат близо до техните флагове.
Ad
решение
Оказва се, че има m-1 начини за разширяване на таблицата, така че взаимното подреждане на представителите и флаговете се променя (ако изключим първоначалното поставяне на таблицата), но има останали m представители.
Ние прилагаме твърдението на Дирихле към решението и означаваме, че представителите са зайци, а някои позиции на масата по време на ротация са клетки. В този случай е необходимо да се направи аналогия между местоположението на представителя до съответния флаг и запълнените клетки. Това означава, че положителен резултат (1 представител е поставен близо до знамето му) е еквивалентен на резултата „заекът е в клетката“. Ние разбираме, че имаме една клетка по-малка от необходимата (m-1), което означава, че един от тях ще има поне 2 зайци. В същото време не се изключват ситуации, че някаква клетка ще бъде празна (нито един представител не съвпада с флага), но в някоя клетка ще има две, три или дори повече зайци (двама, трима или повече представители ще съвпадат с флаговете). По този начин, с една определена ротация, най-малко двама представители ще се окажат близо до знамената си (поне две зайци ще попаднат в една клетка).
Започвайки решаването на такъв проблем, важно е да разберем, че първоначалната позиция е и клетка, но според състоянието на проблема е очевидно празен, така че общата сума се намалява с 1 (m-1).
Пример номер 4. Теория на числата
Принципът на Дирихле в теорията на числата също е от първостепенно значение.
задача
Да предположим, че на една част от тетрадка в клетка, студент случайно в възлите на клетките постави 5 точки. Необходимо е да се докаже, че поне един сегмент с върхове в тези точки преминава през възела на клетката.
решение
Първо трябва да изобразите на лист тетрадка координатната система, основата на която се намира в един от възлите. Осите на координатната система съвпадат с линиите на решетката, а страната на клетката се приема като един сегмент. Оказва се, че всички 5 маркирани точки ще бъдат в системата, а техните координати ще бъдат само цяло число (четно или нечетно). Така получаваме 4 опции на координатите: (четни, четни), (нечетно, четно), (четно, нечетно) и (нечетно; нечетно). Така, 2 от 5 точки ще съответстват на един вариант. Ако погледнете ситуацията от позицията на Дирихле, тогава трябва да посочите точките като зайци, а опциите за координати - като клетки. Получаваме 5 птици с един камък и 4 клетки, съответно, в един от тях ще има най-малко 2 животни. Да предположим, че това са точки P и A, с координати (x 4 , y 3 ) и (x 5 , y 6 ). Средата на сегмента, свързващ тези два върха, ще има координати ((x 4 + x 5 ) / 2), ((y 3 + y 6 ) / 2)), които ще бъдат цели числа при условията на съответния паритет x 4 и x 5, y 3 и y 6 . Оказва се, че средата на сегмента е разположена в клетъчния възел.
Пример номер 5
Доста много задачи с различна сложност могат да бъдат решени чрез принципа на Дирихле. Проблемите с решаването на различни математически и логически въпроси често зависят от този принцип.
задача
На прав път изкопаха малки напречни канали. Разстоянието между всички жлебове е същото и равно на Ö2 м. Необходимо е да се докаже, че независимо от ширината на жлебовете, човек, който се движи по пътя на интервали от 1 м, веднъж ще попадне в една от тях.
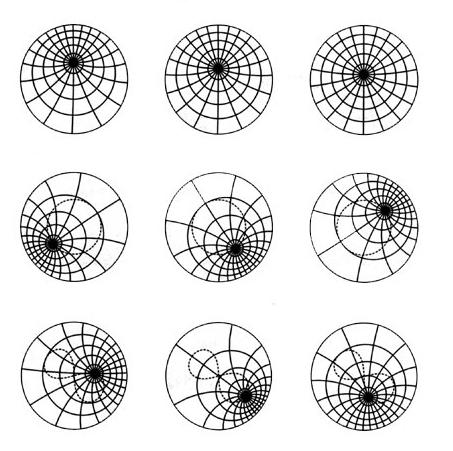
решение
За да се улесни решението, е необходимо да си представим, че пътят може да бъде “навит” върху кръг с дължина Ö2 метра. Оказва се, че всички жлебове ще се сливат в две противоположни, а стъпките на човека ще бъдат изобразени под формата на дъга, равна на 1 м. Трябва последователно да маркираме всички стъпки, докато единият от тях е в дъгата, без значение каква е дължината k дъга (ширина на жлеба). Разбира се, очевидно е, че ако човек е изминал разстояние, равно на по-малко от k, то рано или късно той ще влезе в ров. В края на краищата, човек не може да преодолее разстоянието k, ако дължината му на стъпка е по-малка от k. Така че, трябва да намерим две песни, разстоянието между които няма да надвишава стойността на k. За да направите това, би било подходящо да използвате принципа на Дирихле. Ние психически разделяме целия кръг на дъги с размер по-малък от k и ще ги разглеждаме като клетки. Да предположим, че има n. Да предположим, че броят на стъпките е по-голям от броя на дъгите (n + m), въпреки че няма две стъпки, които да съвпадат поради ирационалността на числото Ö2, тогава според принципа на Дирихле поне една от клетките ще съдържа повече от една стъпка. И тъй като дължината на дъгата е по-малка от k, то разстоянието между стъпките ще бъде по-малко. Затова открихме необходимите стъпки за доказване. 
Обобщение на принципа
Материалите по математика, в допълнение към стандартните (прости и не много) формулировки, също съдържат едно обобщено, което се използва за идентифициране на повече от два обекта, подобни една на друга. Тя твърди, че ако dm + 1 зайци са поставени в d клетки, тогава най-малко m + 1 зайци ще бъдат в една и съща клетка.
Пример № 6. Обобщение
задача
Правоъгълник с площ от 5 x 6 клетки (30 клетки), засенчен само 19. Възможно ли е да се намери квадрат с площ от 2 x 2 клетки, в която поне три ще бъдат боядисани?
решение
Нашата фигура трябва да бъде разделена на 6 блока по 5 клетки. Въз основа на твърдението на Дирихле най-малко 4 клетки ще бъдат нарисувани в една от тях (19/6 = 4). След това в един от квадратите с площ от 4 клетки, разположени в един от блоковете, ще бъдат боядисани най-малко 3 клетки.
Пример номер 7
Клас, в който 25 души. От всеки 3 случайно подбрани ученици двама ще бъдат приятели. Необходимо е да се докаже, че в класа има ученик, който има повече от 11 приятели.
Две решения

Да започнем с това, че приемаме двама ученици, които не са приятелски настроени един към друг (тъй като ако всички бяха приятели един с друг, във всяка тройка ще има трима приятели и всеки ученик щеше да бъде приятел с 24 други). Останалите 23 съученици ще бъдат приятели с един от нашите двама, защото иначе ще има тройка без приятели (а това противоречи на първоначалното състояние на проблема). Оказва се, че един от двамата ученици ще бъде приятел с поне 12 ученици. В този случай учениците са зайци, а термините "приятели или не" са клетки. Имаме 23 животни и само 2 клетки. Съответно, в един от тях най-малко 23/2 = 11,5, т.е. 12 зайци. Това означава, че един от двамата избрани от нас студенти ще бъдат приятели с поне 12 от съучениците си (или дори повече). Разбира се, има и други методи за решаване на проблема, но това е едно от най-разбираемите и удобни.