Тип данни: масиви. Той е прост и елегантен.

При програмирането често се срещат типове данни като масиви. Това е най-простото решение при извършване на подобни операции с голям брой променливи от същия тип. Ако се опитате да напишете програма, която ще включва всички тези данни и повтарящи се изчисления, по-целесъобразно е в продукта да се включи структура, наречена масив, или матрица.

Общата концепция на масивите

Под матрицата (някои по-лесни за представяне под формата на таблица) се разбира последователност от клетки на паметта, в които се съхраняват променливи от същия тип. В този случай връзката между данните и структурата се осъществява чрез едно име и посочения индекс. Той помага да се определи коя променлива да се използва при решаване на проблем.

Трябва ясно да се разбере, че индексът не е съдържанието на клетката. То само сочи към данните, съдържащи се в определена клетка.

Дефиницията на такава структура ще бъде следната: масивите са група данни от един и същ тип, които имат собствено име и съхраняват променливи в последователни клетки от паметта.

Има два вида матрици: едномерна (линейна) и двуизмерна. Първият тип се представя под формата на таблица само с един ред или една колона. В конкретния случай броят на индексите показва размера на матрицата.

Двуизмерен масив е структура, представена като таблица, в която номерът на реда показва първия индекс и номерът на колоната показва втория. По този начин, в матрицата А (m, n), елементът от масив а ₂₃ показва, че тази променлива е във втория ред и в третата колона. А m задава броя на редовете, а n - броя на колоните. Има квадратна матрица (където броят на редовете и колоните е един и същ) и правоъгълна.

Масиви в програмирането

Вече установихме, че масивите са колекция от елементи от един и същи тип. и тип данни трябва да са еднакви в цялата таблица. Всяка структура може да има напълно различен тип данни: числов, низ, символ.

Когато пишете програма, можете да задавате граници по два начина:

• използвайки име на тип, където първата и последната стойност е разделител;
• като се използват предварително обявени константи.

Структурата може да бъде определена и по няколко начина. Бих искал да отбележа, че всеки език на програмата има свой собствен синтаксис. Но принципът на създаване на матрица е подобен. В първия случай специфичен елемент се извиква, използвайки името на променливата на структурата и индекса, посочен в квадратни скоби. В друг случай матрицата може да се определи чрез просто изброяване на всички елементи.

Не бъркайте понятието "индекс" и "тип индекс". Първата дефиниция е посочена в раздела за изразите, за да може да се определи конкретен елемент от масива. Типът индекс се използва само в раздела за описание на структурата. Размерът на масива е посочен в описанието. Много е нежелателно да се променя броят на елементите в процеса на работа по програмата.

Можете да попълните матрици с данни в програмирането по следните начини:

• чрез ръчно въвеждане на клавиатурата;
• използване на генератор на случайни числа;
• когато декларирате масив като константа;
• по дадената формула.

Структуриране на масиви

Масивите са структуриран тип данни. Както вече споменахме, матрицата (ако е двумерна) се състои от ограничен брой редове и колони; ако е линейна, тя е от един ред или една колона, където броят на елементите също е ограничен.

Пресечната точка на ред и колона се нарича клетка. Той съдържа специфични променливи. Не е позволено да има различни типове данни в една таблица. Елементите на масива са променливи с индекси (независимо дали структурата е линейна или двумерна). Индексът е номерът на определена клетка. Той посочва позицията си в таблицата.

Операции с масиви: Добавяне

Така, масивът от данни, който в математиката, че в компютърните науки, е набор от променливи. С него можете да извършвате различни операции: събиране, изваждане, транспониране, умножение, деление.

При добавянето е необходимо да се вземе предвид фактът, че размерите на двете структури трябва да бъдат еднакви. В този случай, ако матриците A и B са дадени с размер MxN, то в получените C = A + B елементи ще бъдат c [i, j] = a [i, j] + b [i, j]. Оказва се, че променливите се добавят по елемент.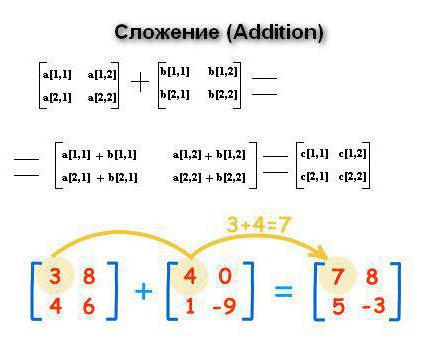

Операции с масиви: изваждане

Тази точка, може би, трябва да започне с премахването на знака минус от матрицата (или, напротив, въведение). Има случаи, когато масивът от данни се състои от елементи, повечето от които са отрицателни. В такава ситуация е за предпочитане минусът да се премести от структурата. За да направите това, пред масата се поставя знак за отрицателен знак и всеки елемент има обратен знак. Нула в този случай е неутрална: тя няма положителен или отрицателен знак.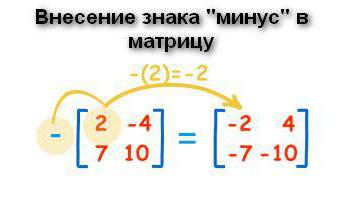

Изваждането се извършва на същия принцип като добавянето. Променлива със същия индекс от друга структура се изважда от първия матричен елемент. Отговорът се записва в третата таблица в съответната позиция.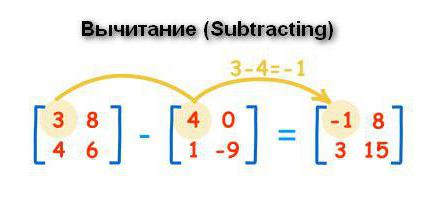

Операции с масиви: Умножение и деление

В допълнение към събирането и изваждането, масив от числа може да се умножи по число, умножава се двете структури заедно, да се разделят един на друг.

За да се намери произведението на матрицата и числото, е необходимо да се умножи всеки елемент от масива с посочения елемент. Отговорът се записва в клетка със същия индекс като първоначалната променлива. 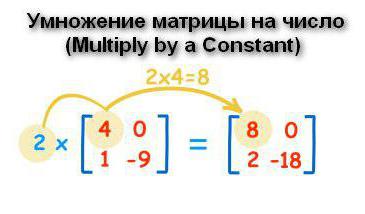За да умножите две матрици помежду си, е необходимо да се придържате към следния алгоритъм.

• Броят на колоните в първата таблица е равен на броя редове от втория множител. В този случай размерът на получената матрица ще бъде както следва: броят на редовете ще бъде равен на броя редове на първия фактор, а броят на колоните ще бъде равен на техния брой от втория фактор.

• Помислете за два фактора.

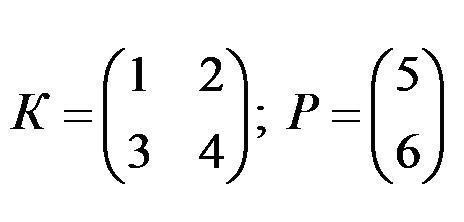
• Тъй като броят на колоните в коефициент K е равен на броя редове в масив P, операцията е възможна. Но ако сменяте матрици на места, тогава законът за промяна на местата на мултипликатори не работи тук. Следователно, P x K е невалиден запис. Ако и двете матрици са квадратни, тогава операцията е възможна и в двата случая.

Формулата за умножение е както следва.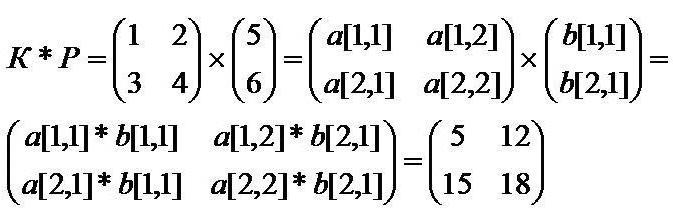

Ако и двата фактора са двуизмерни, следва да се следва принципа, показан на илюстрацията по-долу.

Разделянето се извършва по следната формула. 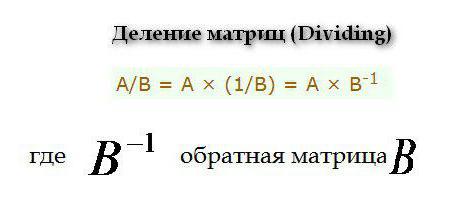Където намирането на обратната матрица (инверсия) се извършва съгласно следната формула.

Транспониране

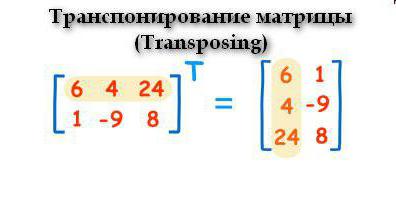
Тази операция се извършва съгласно следния принцип: редовете стават колони. Изглежда така.