Комплексни числа и действия върху тях

Сложните числа , в традиционния смисъл на думата, не са числа, използвани при броенето и измерването, а са математически обекти, които се определят от свойствата, представени по-долу.

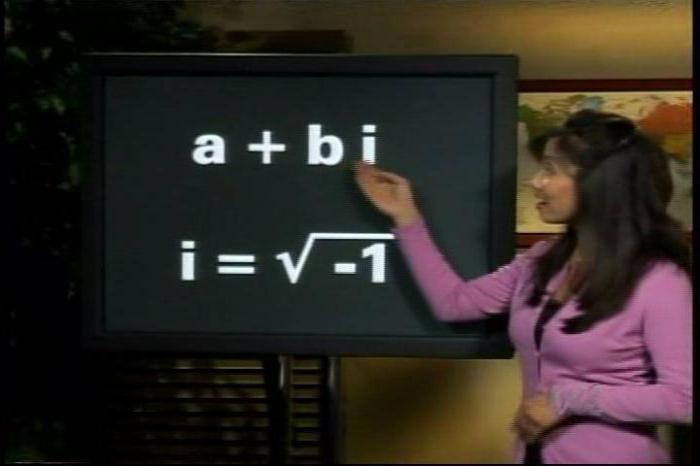
Използвайте 3 форми на комплексно число: алгебрични, експоненциални, тригонометрични.

Алгебрична форма

Сложните числа се обозначават с израза ω + νi, където ω и ν са реални, а символът i се определя от условието i ² - 1 - единицата е въображаема.

Съответно, комплексното число ω + νi е разделено на реалната и въображаемата части. За удобство тя е изобразена в една буква (например η ): η = ω + νi .

Частите на комплексното число η = ω + νi , реално и въображаемо, се обозначават с ω = Reη, ν = съответно.

Комплексните числа се считат за равни, когато техните реални и въображаеми части са еквивалентни. Счита се, че комплексното число е равно на нула, ако неговите части, реални и въображаеми, са равни на нула.

Аритметични операции

допълнение

Сумата от комплексните числа е комплексно число, чиято реална част е еквивалентна на сумата на реалните части, а въображаемото е еквивалентно на сумата на въображаемите части:

η = (ω ₁ + ω ₂ ) + (ν ₁ + ν ₂ ) i.

Казва се, че сред комплекса η ние сме придобили в резултат на добавянето на номерата на комплекса :

η = η ₁ + η _2.

Комплекс η1 и η2 _се наричат ​​термини.

Законите на операцията по добавяне:

1) законът на асоциативността;

2) закон за комутативност ,

Комплексното -ω-bi число се нарича противоположно ω + νi комплексно число. Сумата от противоположните комплексни числа е нула.

разлика

Разликата между комплексните числа се нарича комплексното число η, равно на сумата на числото η ₁ и числото срещу η ₂ :

η = η ₁ + (- η ₂ ) = (ω ₁ -ω ₂ ) + (ν ₁ -ν ₂ ) i.

Смята се, че броят на комплекса η е придобит чрез изваждане на η ₂ и η ₁ (комплексни числа) и е записано:

η = η ₂ -η ₁ .

продукт

Продуктът на комплексните числа е комплексно число:

η = (ω ₁ ω ₂ -ν ₁ ν ₂ ) + (ω ₁ ν ₁ + ω ₂ ν ₁ ) i.

Броят на сложните η се казва, че е получен чрез умножаване на η ₁ с η ₂ (числата η ₁ и η ₂ са комплексни) и пишат:

η = η ₁ η ₂ .

Комплекс η ₁ и η _{2 се} наричат ​​множители.

Законите за умножение на комплексни числа:

1) законът на асоциативността ;

2) закон за комутативност ,

делене

Конкретните комплексни числа се наричат ​​комплексни η такива, че η ₁ = η _1: η ₂ ( η2 0 ) . Частните комплексни числа се изчисляват по формулата:

η = (ω ₁ ω ₂ -ν ₁ ν ₂ ) / (ω ² + ν ² ) + (ω ₁ ν ₁ + ω ₂ ν ₁ ) i / (ω ² + ν ² ).

Числото η се казва, че е получено чрез разделяне на η ₁ от η ₂ и е записано:

η = η ₁ / η _{2 ,}

Добавянето и умножаването на комплексните числа се свързват по правило, наречено дистрибутивен закон за умножение по отношение на добавянето .

Тригонометрични комплексни числа

Използвайте и друга форма на запис на комплексни числа, която се нарича тригонометрична.

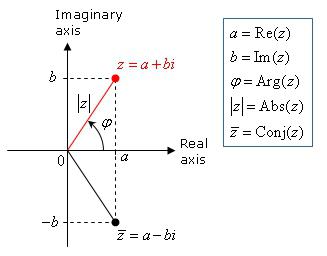
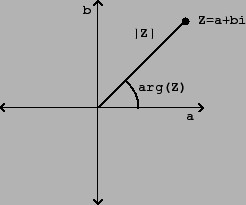
Комплексното число ω + νi може да бъде записано като:

η = k (cosβ + isin), където k ² = ω ² + ν ² .

Този израз е форма на запис на комплексни числа, която се нарича тригонометрична. Модулът на комплексно число е реално число k , а ъгълът β , измерен в радиани, е неговият аргумент.

Ако комплексното число не е нула, тогава неговият модул е ​​положителен; ако η = 0 , с други думи, ω = ν = 0 , тогава неговият модул е ​​равен на нула. Модулът се определя еднозначно.

Продуктът на тригонометричните комплексни числа е модулът на комплексното число, което е еквивалентно на произведението на факторите, или по-скоро на техните модули, и аргументът е еквивалентен на сумата от аргументите на факторите:

η ₁ η ₂ = k ₁ k ₂ [cos (β ₁ + β ₂ ) + isin (β ₁ + β ₂ )].

Частните тригонометрични комплексни числа, които не са нула, са сложно число, модулът на който е еквивалентен на частичния дивидент и делител (на техните модули), а аргументът е еквивалентен на разликата между аргументите на дивидента и делителя:

η ₁ / η ₂ = k ₁ / k ₂ [cos (р1-р2) + изоин (р1-р2)].

Естествената степен на броя на комплекса

В математиката n-тата мощност на комплекс η е комплексът w, който се намира в резултат на умножението на комплекса n пъти сам по себе си: w = ηη ... η .

Обикновено използват по-кратък запис:

w = η ⁿ ,

в която броят η е в основата на степента, а n (естественото число) е експонентата.

N-тата мощност на η (комплексно число), която е дадена в тригонометрична форма, се изчислява по формулата:

η ⁿ = kn (cosnβ + isinnβ).

Тази формула се нарича формула на Moivre.