Постоянната на Болцман: значение и физически смисъл
Като точна количествена наука, физиката не може да направи без набор от много важни константи, включени като универсални коефициенти в уравненията, които установяват връзка между тези или други величини. Това са фундаментални константи, поради които такива отношения придобиват инвариантност и са способни да обяснят поведението на физическите системи в различен мащаб.
Сред тези параметри, които характеризират свойствата, присъщи на нашата Вселена, е константата на Болцман, количество, включено в редица от най-важните уравнения. Въпреки това, преди да се обърне към разглеждане на неговите характеристики и значения, е невъзможно да не кажем няколко думи за учения, чието име носи.
Лудвиг Болцман: научна заслуга
Един от най-великите учени от XIX век, австрийският Лудвиг Болцман (1844–1906) допринесе значително за развитието на молекулярната кинетична теория, ставайки един от основателите на статистическата механика. Той е автор на ергодичната хипотеза, статистическият метод в описанието на идеален газ, основното уравнение на физичната кинетика. Той работи много по въпросите на термодинамиката (теорема H-Boltzmann, статистически принцип за втория закон на термодинамиката), радиационна теория (закон Стефан-Болцман). Той също така се занимава с някои въпроси на електродинамиката, оптиката и други отрасли на физиката в своите творби. Името му е обезсмъртено в две физически константи, което ще бъде разгледано по-долу.
Лудвиг Болцман е твърд и последователен поддръжник на теорията за атомно-молекулярната структура на материята. През годините той бил принуден да се бори с липсата на разбиране и отхвърляне на тези идеи в научната общност на времето, когато много физици разглеждали атомите и молекулите като ненужна абстракция, в най-добрия случай, като условно устройство за удобство на изчисленията. Болезнената болест и атаките на консервативно настроените колеги предизвикаха тежка депресия в Болцман, която не можеше да понесе изключителния учен, извършил самоубийство. На надгробния паметник, над бюста на Болцман, като признак за признаване на неговите заслуги, изважда се уравнението S = k out logW - един от резултатите от неговата плодотворна научна дейност. Константата k в това уравнение е константата на Boltzmann.

Молекулна енергия и температура на веществото
Концепцията за температурата служи за характеризиране на степента на топлина на тялото. Във физиката се използва абсолютна температурна скала, основана на заключението на молекулярната кинетична теория на температурата като мярка, отразяваща енергията на топлинното движение на частиците на дадено вещество (разбира се, средната кинетична енергия на множество частици).
Както Joule, приет в системата SI, така и ергът, използван в GHS системата, са твърде големи единици за изразяване на енергията на молекулите и всъщност е много трудно да се измери температурата по този начин. Удобната единица за температура е степента, а измерването се извършва индиректно, чрез регистриране на променящите се макроскопични характеристики на веществото - например обем.

Как се осъществява енергията и температурата
За изчисляване на състоянията на реална субстанция при близки до нормалите температури и налягания, идеалният газов модел се използва успешно, т.е. молекула, чийто размер е много по-малък от обема, зает с определено количество газ, а разстоянието между частиците значително надвишава радиуса на тяхното взаимодействие. Въз основа на уравненията на кинетичната теория, средната енергия на такива частици се определя като Е cf = 3/2 T kT, където Е е кинетичната енергия, Т е температурата, а 3/2 is k е коефициентът на пропорционалност, въведен от Болцман. Числото 3 тук характеризира броя на степените на свобода на транслационното движение на молекули в три пространствени измерения.
Количеството k, което по-късно е кръстен на австрийския физик като константа на Болцман, показва коя част от джаула или ерг съдържа една степен. С други думи, неговата стойност определя как средно статистически се увеличава енергията на топлинното хаотично движение на единична частица от едноатомния идеален газ, когато температурата се повиши с 1 градус.
Колко пъти е степента по-малка от джаула
Числената стойност на тази константа може да бъде получена по различни начини, например чрез измерване на абсолютната температура и налягане, като се използва уравнението на идеалния газ, или като се използва моделът на броуновското движение. Теоретичното извеждане на това количество на сегашното ниво на познание не е възможно.
Константата на Болцман е равна на 1.38 × 10 -23 J / K (тук K е келвин, степен на абсолютна температурна скала). За колективните частици в 1 мол идеален газ (22,4 литра), коефициентът на свързваща енергия с температура (универсална газова константа) се получава чрез умножаване на константата на Болцман с числото на Авогадро (броя на молекулите в мол): R = kN A , и е 8.31 J / (mol vin Келвин). Въпреки това, за разлика от последната, константата на Болцман е по-универсална по своята същност, тъй като тя влиза и в други важни отношения, а също така служи и за определяне на друга физическа константа.
Статистическо енергийно разпределение на молекулите
Тъй като състоянията на материята с макроскопичен ред са резултат от поведението на голям набор от частици, те се описват чрез статистически методи. Последното включва откриване как се разпределят енергийните параметри на газовите молекули:
- Максвелово разпределение на кинетичните енергии (и скорости). Това показва, че в един газ в равновесие повечето от молекулите имат скорости, близки до някои от най-вероятните скорости v = √ (2kT / m 0 ), където m 0 е масата на молекулата.
- Болцманово разпределение на потенциалните енергии за газове, които са в полето на всякакви сили, като гравитацията на Земята. Тя зависи от съотношението на два фактора: привличане към Земята и хаотично топлинно движение на газови частици. В резултат на това, колкото по-ниска е потенциалната енергия на молекулите (по-близо до повърхността на планетата), толкова по-висока е тяхната концентрация.
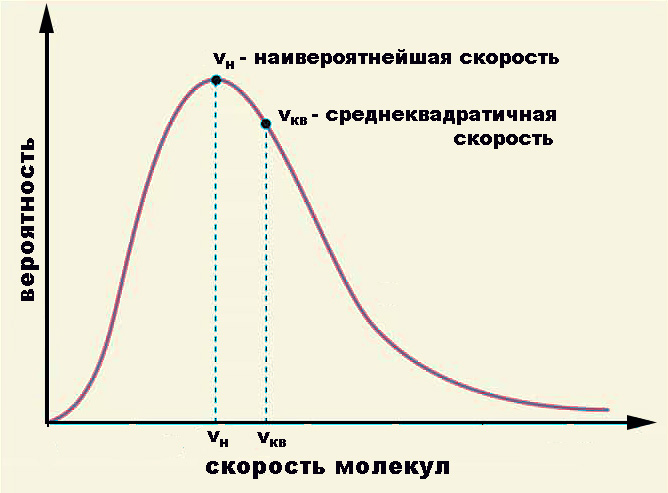
И двата статистически метода са комбинирани в разпределението на Максуел - Болцман, който съдържа експоненциалния коефициент e - E / kT , където Е е сумата на кинетичните и потенциалните енергии, а kT е средната енергия на познатото ни топлинно движение, контролирано от постоянната на Болцман.
Постоянна k и ентропия
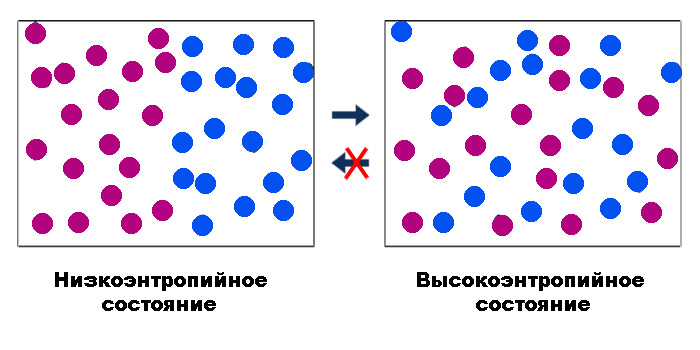
В общ смисъл ентропията може да се характеризира като мярка за необратимостта на термодинамичния процес. Тази необратимост е свързана с разсейване - разсейване на енергия. Със статистическия подход, предложен от Болцман, ентропията е функция от броя на начините, по които дадена физическа система може да бъде реализирана, без да се променя нейното състояние: S = k n lnW.
Тук константата k задава мащаба на растежа на ентропията с увеличаване на това число (W) на вариантите на системата или на микростатутите. Макс Планк, който доведе тази формула до съвременната форма и предложи да се даде на константата k името на Болцман.
Законът на радиацията на Стефан - Болцман
Физическият закон, който установява как енергийната осветеност (мощност на излъчване на единица повърхност) на абсолютно черно тяло зависи от неговата температура, има формата j = σT 4 , т.е. тялото излъчва пропорционално на четвъртата сила на неговата температура. Този закон се използва, например, в астрофизиката, тъй като излъчването на звезди е близко по характер спрямо черното тяло.
В това съотношение има още една константа, която също контролира мащаба на явлението. Това е константата Стефан - Болцман σ, която е приблизително 5.67 × 10 -8 W / (m 2 K 4 ). Неговото измерение включва Келвин - това означава, че е ясно, че постоянната на Болцман к също участва тук. В действителност, величината σ се определя като (2π 2 4 k 4 ) / (15c 2 h 3 ), където c е скоростта на светлината, а h е константата на Планк. Така константата на Болцман, комбинирана с други световни константи, образува количество, отново свързващо енергия (мощност) и температура между тях - в този случай по отношение на радиацията.

Физическата същност на константата на Болцман
Вече беше отбелязано по-горе, че константата на Болцман е една от така наречените основни константи. Въпросът е не само, че ни позволява да установим връзка между характеристиките на микроскопичните явления на молекулярното ниво и параметрите на процесите, наблюдавани в макросвета. И не само, че тази константа е включена в редица важни уравнения.
Понастоящем не е известно дали има някакъв физически принцип, въз основа на който би могъл да се извлече теоретично. С други думи, от нищо не следва, че стойността на дадена константа трябва да бъде точно това. Можем да използваме други стойности и други единици вместо градуси като мярка за съответствието на кинетичната енергия на частиците, след това числовата стойност на константата ще бъде различна, но ще остане постоянна стойност. Заедно с други фундаментални ценности от този вид - ограничаващата скорост c, константата на Планк h, елементарната такса e, гравитационната константа G - науката приема константата на Болцман като даденост на нашия свят и използва за теоретичното описание на физическите процеси, протичащи в него.