Ускорение на гравитацията: откриване, причини, формула
Ускоряването на свободното падане е едно от многото открития на великия Нютон, който не само обобщава опита на своите предшественици, но и дава строго математическо обяснение на огромно количество факти и експериментални данни.
Предпоставки за откриване. Галилееви експерименти
Един от многото експерименти на Галилео Галилей беше посветен на изучаването на движението на тела в полет. Преди това в световната система преобладаваше мнението, че по-леките тела падат по-бавно от тежките. Хвърляне на различни обекти от височина Наклонената кула, Галилео откри, че ускорението на свободното падане за тела с различна маса е точно същото. 
Галилео правилно приписва леките несъответствия между теорията и експерименталните данни на влиянието на въздушното съпротивление. За да докаже своето разсъждение, той предложи да повтори експеримента във вакуум, но по това време нямаше техническа възможност за това. Само много години по-късно мисленият експеримент на Галилео Исак Нютон.
Теория на Нютон
Чест на откритието закона на света принадлежи на Нютон, но самата идея е във въздуха за около 200 години. Основната предпоставка за формирането на нови принципи на небесната механика стана законите на Кеплер, формулирани от него на базата на многогодишни наблюдения. От океана на предположения и догадки Нютон извадил предположението за силата на гравитацията на Слънцето и разширил теорията си за понятието за разширение на света. Той провери хипотезата си за обратната пропорционалност на силата с квадрата на разстоянието, като е разгледал орбитата на Луната. Последващите тестове на тази идея бяха извършени чрез изследване на движението на спътниците на Юпитер. Резултатите от наблюденията показаха, че същите сили действат между сателитите на планетите и самите планети, както във взаимодействието на Слънцето и планетите. 
Откриване на гравитационния компонент
Силата на гравитацията на Земята към Слънцето се подчинява на формулата:
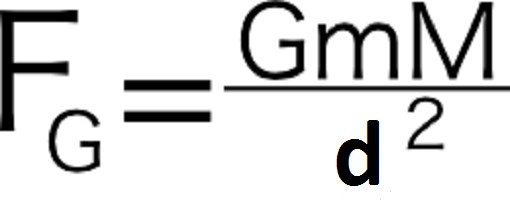
Експериментите показват, че фактор 1 / d 2 в тази връзка е напълно приложимо в случай на разглеждане на други планети в Слънчевата система. Постоянната G е коефициентът, който довежда стойността на пропорцията до цифрова стойност.
Воден от собствената си теория, Нютон измерва масовите съотношения на различни небесни тела, като масата на Юпитер / масата на Слънцето, масата на Луната / масата на Земята, но Нютон не може да даде цифров отговор на въпроса колко тежи Земята, тъй като константата G все още остава. неизвестен.
стойност гравитационна константа е открита едва половин век след смъртта на Нютон. Оценките на тази стойност въз основа на хипотези, подобни на предположенията на Нютон, показват, че тази стойност е незначителна и е почти невъзможно да се изчисли стойността му при земни условия. обичаен притегляне Изглежда огромно, защото всички познати ни обекти са невероятно малки в сравнение с масата на земното кълбо.
Краят на 18-ти век. G измерване
Първите опити за измерване на G са извършени в края на 18-ти век. Като теглителна сила те използваха огромна планина. Оценката на ускорението на свободното падане е направена въз основа на отклонението от вертикалата на тежестта на махалото, разположено в непосредствена близост до планината. С помощта на геоложки данни бяха оценени масата на планината и нейното средно разстояние от махалото. Така получихме първото, доста грубо измерение на тайнствената константа.
Размери на лорд Кавендиш
Лорд Кавендиш, в своята лаборатория, извърши измервания на гравитационното привличане чрез метода на свободно претегляне. 
За експериментите е използвана метална топка и масивно парче метал. Кавендиш прикрепи малки тънки топчета към тънка дъска и им донесе големи оловни топки. В резултат на удара дъската се извива, докато ефектът от привличането компенсира силите на Hooke. Експериментът беше толкова фин, че дори и най-малкият дъх на вятъра можеше да унищожи резултатите от изследванията. За да избегне конвекция, Кавендиш постави цялото измервателно оборудване в голяма кутия, после го постави в затворено помещение и наблюдава експеримента с телескоп.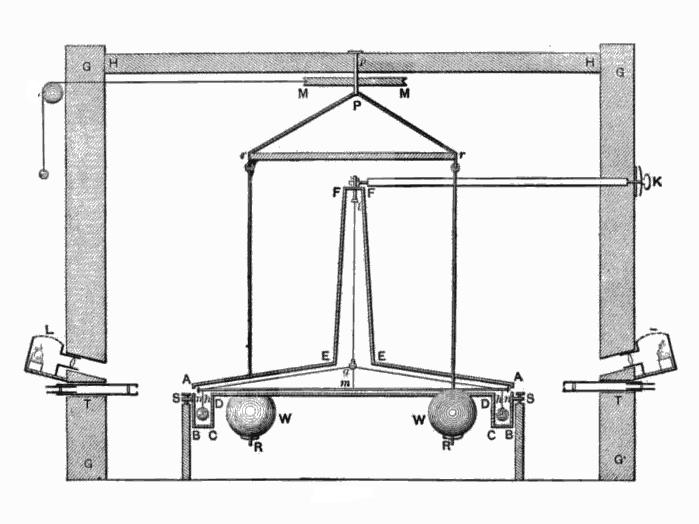 
Изчислявайки силата на завъртане на нишката, Кавендиш изчисли стойността на G, която впоследствие беше леко коригирана поради други, по-точни експерименти. В съвременната система от единици:
G = 6.67384 × 10 -11 m 3 kg -1 s -2 .
Тази стойност е една от малкото физически константи. Неговата стойност е неизменна във всяка точка на Вселената.
Измерване на земното ускорение
Според третия закон на Нютон силата на привличане на две тела зависи само от тяхната маса и разстоянието между тях. По този начин, замествайки в дясната част на уравнението познат множител от втория закон на Нютон, получаваме:
ma = G (mM) / d2.
В нашия случай масата m може да бъде намалена, а величината а е ускорението, с което тялото m е привлечено от Земята. В момента ускорението на гравитацията обикновено се обозначава с буквата g. Получаваме:
g = GM / d2.
В нашия случай d е радиусът на Земята, M е неговата маса, а G е най-неуловимата константа, която физиците търсят от много години. Подменяйки известните данни в уравнението, получаваме: g = 9.8m / s 2 . Тази стойност е ускорението на свободното падане на Земята. 
G стойности за различни географски ширини
Тъй като нашата планета няма формата на топка, а е геоид, радиусът му не винаги е един и същ. Земята е сплескана, така че ускорението на свободното падане ще има различни стойности на екватора и на двата полюса. Като цяло разликата в показанията на дължината на радиуса е около 43 км. Следователно, във физиката, за решаване на проблемите се взема ускорението, дължащо се на гравитацията, което се измерва на ширина около 45 0 . Често, за да се улеснят изчисленията, се приема, че е 10 m / s 2 .
G стойност за луната
Нашият спътник се подчинява на същите закони като останалите планети в Слънчевата система. Строго погледнато, при изчисляване на ускорението на повърхността на Луната, трябва да се вземе предвид и привличането от слънцето. 
Но, както може да се види от формулата, с увеличаване на разстоянието, стойността на силата на привличане намалява рязко. Следователно, отхвърляйки всички вторични сили, използвайте същата формула:
G L = GM / d 2 .
Тук М е масата на луната, а d е нейният диаметър. Подменяйки известните стойности, получаваме стойността на G L = 1,622 m / s 2 . Тази стойност е ускорението на свободното падане на Луната.
Това е толкова малка стойност на G L, че е основната причина за отсъствието на атмосфера на Луната. Според известна информация, в зората на нашия сателит имаше атмосфера, но поради слабата атракция Луната бързо я загуби. Всички планети с голяма маса обикновено имат собствена атмосфера. Ускоряването на свободното падане е достатъчно голямо, за да не само да не загубят собствената си атмосфера, но и да вземат известно количество молекулен газ от космоса.
Нека обобщим някои резултати. Ускорението, дължащо се на гравитацията, е количеството, което притежава всяко материално тяло. Без значение колко изненадващо звучи, но всичко, което има маса, привлича околните обекти към себе си. Просто тази атракция е толкова малка, че няма значение в ежедневието. Въпреки това учените са сериозни дори и за най-малките физически константи, защото въздействието, което те имат върху света около нас, не е напълно изяснено.