Какъв е принципът на фермата?
XVII век е белязан от бързото развитие в Европа на специален раздел на физиката - оптика. Законите на отражението и пречупването бяха отворени за светлина и принципът на Ферма показа защо те имат подходящата математическа форма. Нека видим по-подробно какво е този принцип.
Явления на пречупване и отражение

Чрез размисъл те разбират явление, при което светлината, която се разпространява в вещество, прозрачно за нея, се сблъсква с пречка по пътя си и драстично променя своята траектория. Всяко препятствие може да бъде всяко: течно или твърдо, прозрачно и непрозрачно.
Явлението размисъл е известно още от древни времена. Според историческите доказателства, законите за размисъл вече са били формулирани преди нашата ера. И през първия век от н.е., египетският философ Херън от Александрия изразява идеята за траекторията на светлината, която френският Пиер Ферма по-късно използва при формулирането на своя принцип.

Феноменът на пречупване е разрушаването на права линия, по която се движи светлината, когато пресича повърхността, разделяща два прозрачни материала. Имайте предвид, че в случай на отражение, лъчът се движи в един прозрачен материал или, както се казва, в една среда.
Първата формулировка на законите на пречупване се приписва на персийските математици от 10-ти век, на някой Ибну Сал, който в творбите си се основава на произведенията на Клавдий Птолемей (I-II в.). В края на XVI - началото на XVII в. Холандският учен Снел, обобщавайки резултатите от много експерименти със светлина, формулирал математически във втория закон на пречупването, който сега носи неговото фамилно име. Снел даде думите си на разстояние, а не на ъгъл, както е прието сега. Съвременният облик на закона за пречупване вече даде Рене Декарт.
Законите за разпространение на светлината в прозрачни среди
Преди да пристъпим към разглеждане на принципа на Ферма, трябва да формулираме законите на пречупване и отражение на светлината. За всяко от тези явления е обичайно да се избират два закона. По-долу са комбинирани по двойки:
- Траекторията на лъча, когато пресича интерфейса между две среди, винаги лежи в същата равнина като нормалната към равнината на тази граница. Възможната траектория на лъча се формира в общия случай от три части: падащият лъч, пречупен и отразен.
- Ако ъгълът между падащия светлинен лъч и нормата се нарича θ 1 , същият ъгъл, но за отразения лъч, се записва като θ 2 , а пречупеният ъгъл е θ 3 , тогава вторият закон ще изглежда така:
- за отражение: θ 1 = θ 2 ;
- за пречупване: n 1 * sin (θ 1 ) = n 2 * sin (θ 3 ).
В тези формули n 1 и n 2 са показатели на пречупване в прозрачни среди 1 и 2. Индексът на пречупване по дефиниция се изчислява, както следва:
n = c / v.
Тук v и с са скоростите на движение на светлинния лъч в средата и във вакуум.
Формулирането на принципа на стопанството

Пиер Ферма е един от най-известните математици и адвокати на Франция през първата половина на XVII век. Принципът, който носи неговото име, той формулира през 1662 г., т.е. половин век след като Снел открил закона си за пречупване.
Накратко, принципът на Ферма може да бъде формулиран по следния начин: светлината, когато се движи в абсолютно всяка прозрачна среда, избира такава траектория, която преминава в най-кратко време.
Всъщност, тази формулировка не се различава от тази, която Херон от Александрия прави една и половина хиляди години по-рано за феномена на размисъл. Въпреки това французинът го прави общ за всички явления, свързани със светлината, и показва как законите на пречупване и размисъл могат да бъдат извлечени от този принцип.
Заключение на първия закон за размисъл
Използвайки принципа на Ферма, законите на отражението ще бъдат получени математически. За да направите това, разгледайте фигурата по-долу.
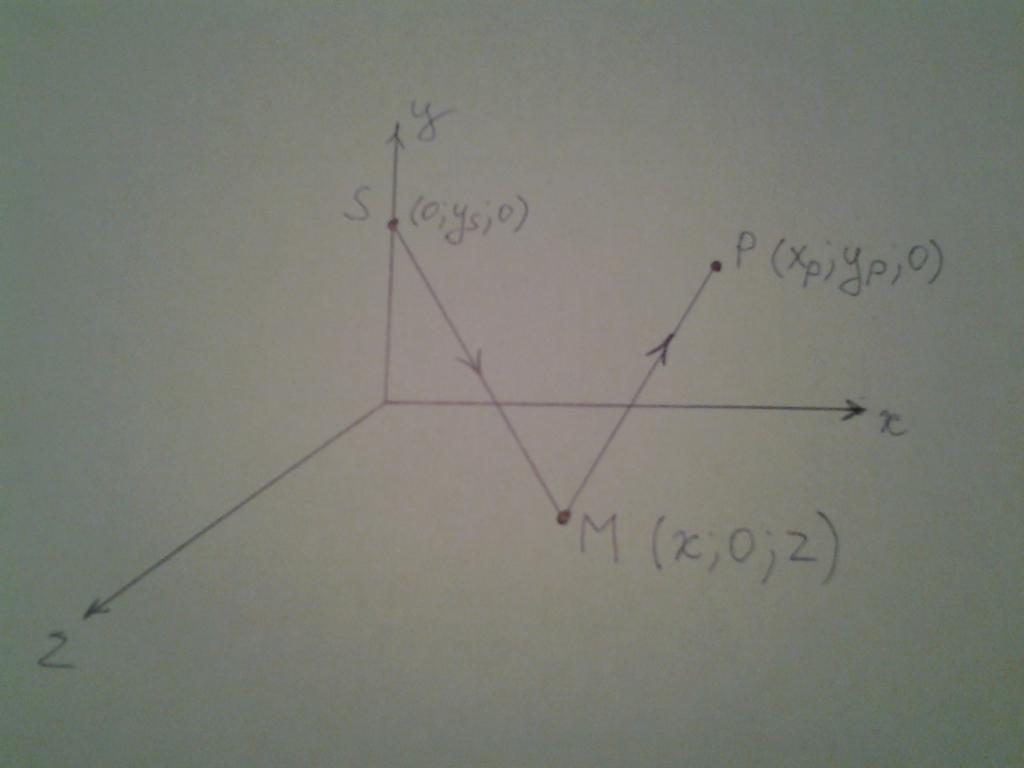
Тук е показано, че лъчът излиза от точка S, която лежи по оста y. Тогава тя се отразява от равнината xz в някаква неизвестна точка М. След отражение, лъчът се премества в точката Р, разположена на равнината xy. Избраната позиция на точките S и P не оказва влияние върху общия характер на допълнителните разсъждения, а само опростява математическите изчисления.
Затова записваме координатите на всяка точка:
S (0; yS; 0);
M (x; 0; z);
Р (х Р ; у Р ; 0).
Координатите на позициите на точките S и P са известни. Задачата е да се намери такава точка M, която да съответства на реалния път SMP, преминаван от светлинния лъч. Предполагаме също, че разглежданото пространство е хомогенно, т.е. скоростта на светлината във всяка точка е постоянна стойност.
Според принципа на Ферма, траекторията на SMP светлина ще премине в най-краткия срок, ако е възможно най-кратък. Пишем дължината му:
SM = x (x2 + yS2 + z2); МР = √ ((хх Р ) 2 + у Р 2 + z 2 );
SMP = √ (x 2 + y S 2 + z 2 ) + √ ((xx P ) 2 + y P 2 + z 2 ).
За да се изчисли минималната дължина на SMP, е необходимо да се намерят частичните производни по отношение на x и z (неизвестните координати на точката M) и да се приравнят получените резултати до нула.
Първо откриваме частичното производно по z. Имаме:
∂ (SMP) / =z = z / √ (x 2 + y S 2 + z 2 ) + z / √ ((xx P ) 2 + y P 2 + z 2 ) = 0.
Това равенство има един корен при z = 0. С други думи, точката М лежи на оста х, тоест в същата равнина като точките P и S (равнината xy). От което следва, че възстановената нормална до xz равнина, в която, чрез условието на задачата, точката М се намира, ще лежи със SM и MP в една и съща равнина (xy). Това е първият закон за размисъл.
Заключение на втория закон за размисъл
Продължете да изчислявате предишния елемент. Както беше казано, сега е необходимо да се намери частичното производно по отношение на х. Имаме:
SM (SMP) / =x = x / √ (x 2 + y S 2 + z 2 ) + (xx P ) / √ ((xx P ) 2 + y P 2 + z 2 ) = 0.
Ние пишем последното равенство във формата:
x / SM + (xx P ) / MP = 0 =>
x / SM = (x P -x) / MP.
Отношенията, получени във всяка част на равенството, са синусите на ъглите с връх в точките S и P. Ако сега възстановим нормалността до xz равнината през точката M, тогава маркираните ъгли ще съответстват на ъглите на падане (между SM и норма) и отражения (между MP и норма) ,
Така, следвайки принципа на Ферма, получихме и втория закон за отражение на светлината.
Заключение на закона за пречупване на Snell
Сега нека покажем как законът на пречупването на светлината може да се извлече от принципа на Ферма. За да направите това, помислете за картина, подобна на предишната.
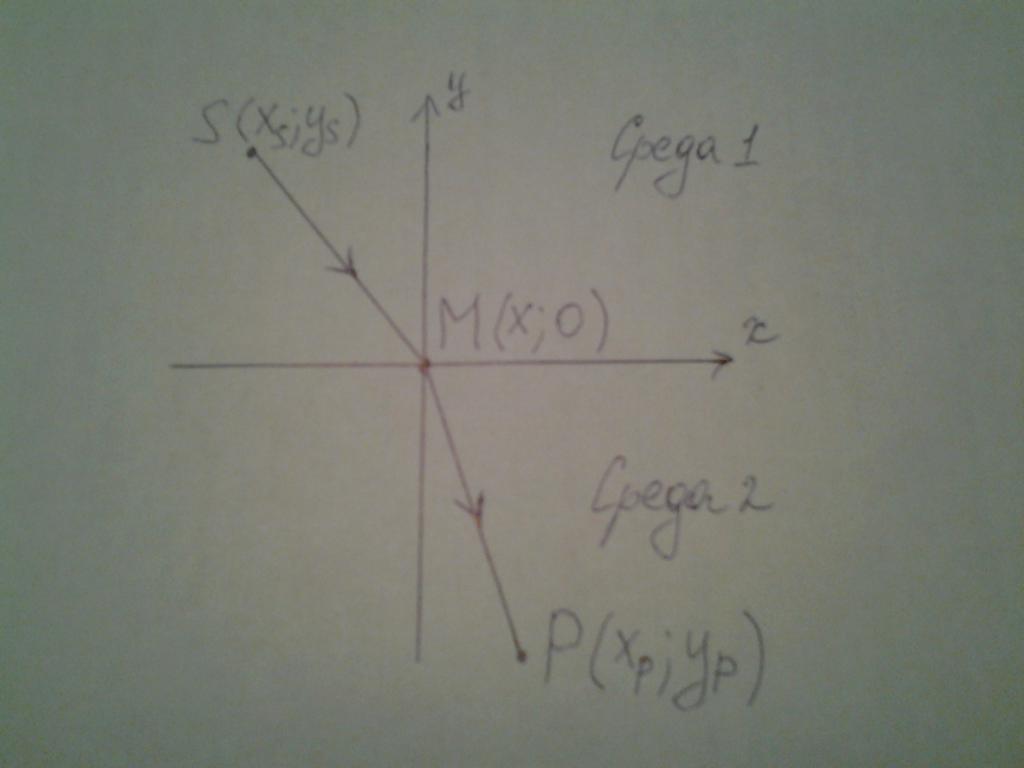
За простота ще разгледаме случая в равнината xy. Записваме координатите на източника S и приемника P light, които са в различни среди:
S (xS; yS);
М (х; 0);
P ( xP ; yP).
Нека намерим неизвестната координата на точката М. Координатът y = 0 е точно известен с него, тъй като именно на границата на средата (ос x) скоростта на светлината се променя. Дължините на сегментите SM и MP са равни на:
SM = x (xx S ) 2 + y S 2 );
МР = Х (х Р- х) 2 + у Р 2 ).
Общото време, което светлината прекарва по траекторията на SMP, ще бъде равно на:
t = SM / v1 + MP / v2.
Тук v 1 и v 2 са скоростите на лъча в съответната среда. За да намерим минималното време на движение, трябва да вземем цялата производна по отношение на променливата x и да я приравним към нула. Получаваме:
dt / dx = (xx S ) / (√ (xx S ) 2 + y S 2 ) * v 1 ) - (x P -x) / (√ (x P -x) 2 + y P 2 ) * v 2 ) = 0 =>
(xx S ) / (SM * v 1 ) = (х Р- х) / (МР * v2).
Използвайки функциите на синусите на ъгъла на падане θ 1 и пречупването θ 3 , получаваме:
sin (θ 1 ) / v 1 = sin (θ 3 ) / v 2 .
За да се приведе полученото равенство в закона Снел в удобна форма (чрез рефракционните индекси на средата), е необходимо левата и дясната страни да се умножат със скоростта на светлината c.

По този начин прилагането на принципа на Ферма улеснява извеждането на закони за основните явления на движение на светлинния лъч в прозрачни материали.
Движението на светлината в нехомогенна среда
Разгледаните по-горе случаи предполагат, че материалът е хомогенен и светлинният лъч запазва скоростта си, когато се движи. В случая на нехомогенни среди е вярно следното равенство:
L = (n (x, y, z) * dl.
Този интеграл се взема по траекторията на светлината. Диференциалът dl е сегмент от пътя, за който средата запазва своята хомогенност. Стойността n (x, y, z) е локален индекс на пречупване.
Отбелязаният интеграл обикновено се нарича интегрален оптичен път. Принципът на фермата за оптичния път включва намиране на крайности за L.
Общата формулировка на разглеждания принцип
Принципът на минимално време за движение на светлината е специфичен за по-обща формулировка. Понастоящем генерализираният принцип на Ферма е формулиран по следния начин: светлината избира траектория по време на движение, която съответства на екстремумите на оптичния път.
Екстремумите на дадена функция, според математическа дефиниция, са минималната, максималната и инфлексната точка. Общият принцип на Ферма удовлетворява всички тези стойности, т.е., траекторията на светлината не е задължително да бъде минимална, тя може да бъде както максималната, така и съответната точка на инфлексия на оптичния път.
Вътрешна аналогия с разглеждания принцип
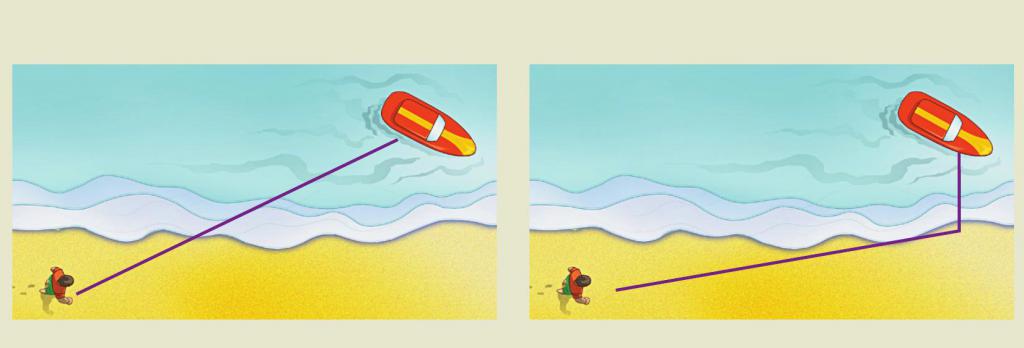
Общият принцип на Ферма, от своя страна, е специален случай на така наречения принцип на най-малкото действие. Тук няма да дадем съответните дефиниции и техните математически формулировки, но нека покажем къде може да се приложи принципът, предложен от французите.
Той се използва за решаване на проста, на пръв поглед, ежедневна задача: например човек се удавя в морето близо до плаж. Как трябва спасителят да се движи по брега, за да спаси удавник? Разбира се, той трябва да дойде на помощ най-малко време. Тъй като скоростта на движение на спасителя на плажа е повече, отколкото на водата, той трябва да измине известно разстояние по брега и едва след това да скочи във водата и да плува. Това означава, че задачата се свежда до прилагането на принципа на Ферма, където ролята на светлинния лъч се играе от спасителя.
Имайте предвид, че решението на този проблем не е просто, защото в неговия процес се появяват уравнения от 4-та степен.
По този начин принципът на Ферма е инструмент за получаване на основните закони на разпространението на светлината. Но това не е фундаментално. Може да се каже, че той следва от принципа на Хюйгенс за източници на вторични сферични вълни.