Какви са методите за оптимизация? Методи за оптимизиране на управленските решения

Най-приемливо решение, което се взема на управленско ниво по отношение на всеки въпрос, се счита за оптимално, а процесът на неговото търсене се счита за оптимизация.

Взаимозависимостта и сложността на организационните, социално-икономическите, техническите и други аспекти на управлението на производството сега се свеждат до вземане на управленски решения, които засягат голям брой различни фактори, които са тясно свързани помежду си, което прави невъзможно да се анализира всеки един поотделно, използвайки традиционен аналитичен анализ. методи.

Повечето от факторите са решаващи в процеса на вземане на решения и те (по същество) не подлежат на никаква количествена характеристика. Има и такива, които са практически непроменени. В тази връзка е необходимо да се разработят специални методи, които да осигурят подбора на важни управленски решения в рамките на комплексни организационни, икономически, технически задачи (експертни оценки, оперативни изследвания и методи за оптимизация и др.).

Използват се методи за проучване на операциите, за да се намерят оптимални решения в такива области на управление като организацията на производствените и транспортни процеси, мащабното планиране производство, материал и техническото снабдяване.

Методите за оптимизиране на решенията трябва да бъдат изследвани чрез сравняване на числените оценки на редица фактори, анализът на които по традиционни методи не може да бъде направен. Оптималното решение е най-доброто от възможните варианти икономическа система и най-приемливите по отношение на отделните елементи на системата са неоптимални.

Същността на операциите на изследователските методи

Както бе споменато по-рано, те формират методите за оптимизиране на управленските решения. Техните основи са математически (детерминистични), вероятностни модели, представящи разглеждания процес, дейност или система. Този вид модел представлява количествена характеристика на съответния проблем. Те служат като основа за вземане на важни решение за управление в процеса на търсене оптимално приемлива опция.

Списъкът на въпросите, които играят важна роля за преките мениджъри на производството и които се решават в хода на използването на разглежданите методи:

• степента на валидност на избраните решения;
• колко по-добри са те от алтернативни;
• степен на отчитане на определящите фактори;
• какъв е критерият за оптималност на избраните решения.

Тези методи за оптимизиране на решенията (мениджърски) са насочени към намиране на оптимални решения за възможно най-много фирми, фирми или техни подразделения. Те се основават на съществуващите постижения на статистическите, математическите и икономическите дисциплини (теория на игрите, опашка, графики, оптимално програмиране, математическа статистика).

Методи за експертна оценка

Тези методи за оптимизиране на управленските решения се прилагат, когато задачата е частично или изцяло не подлежи на формализиране, а нейното решение не може да бъде намерено с помощта на математически методи.

Експертизата е изучаването на сложни специфични въпроси на етапа на разработване на конкретно управленско решение от съответните лица, които притежават специална база от знания и впечатляващ опит за получаване на заключения, препоръки, мнения, оценки. В процеса на експертни изследвания, най-новите постижения на науката и технологиите се използват като част от специализацията на експерта.

Разглежданите методи за оптимизиране на редица управленски решения (експертни оценки) са ефективни при решаване на следните управленски задачи в производствения сектор:

1. Изследването на сложни процеси, явления, ситуации, системи, които се характеризират с неформализирани, качествени характеристики.
2. Класиране и определяне според даден критерий на значими фактори, които са решаващи за функционирането и развитието на производствената система.
3. Разглежданите методи за оптимизация са особено ефективни в областта на прогнозиране на тенденциите в развитието на производствената система, както и нейното взаимодействие с външната среда.
4. Подобряването на надеждността на експертните оценки е насочено предимно към целевите функции, които са количествени и качествени, като осредняват мненията на квалифицираните специалисти.

И това са само някои от методите за оптимизиране на редица управленски решения (партньорска проверка).

Класификация на разглежданите методи

Методи за решаване на оптимизационни задачи, базирани на броя на параметрите, могат да бъдат разделени на:

• Методи за едномерна оптимизация.
• Методите за оптимизация са многомерни.

Те се наричат ​​още "методи за числено оптимизиране". За да бъдем точни, това са неговите алгоритми за търсене.

В рамките на прилагането на деривативни методи са:

• методи за директна оптимизация (нулев ред);
• градиентни методи (първи ред);
• методи от втори ред и др.

Повечето от многомерните оптимизационни методи са близки до проблема на втората група методи (едномерна оптимизация).

Унивариатни техники за оптимизация

Всички методи за числено оптимизиране се основават на приблизително или точно изчисляване на неговите характеристики, като например стойностите на целевата функция и функциите, които определят допустимия набор, техните производни. По този начин, за всяка отделна задача, въпросът за избора на характеристики за изчислението може да бъде решен в зависимост от съществуващите свойства на въпросната функция, наличните възможности и ограниченията при съхранението и обработка на информация.

Съществуват следните методи за решаване на оптимизационни задачи (едномерни):

• Метод на Фибоначи;
• дихотомия;
• златна част;
• двойна стъпка.

Метод на Фибоначи

Първо трябва да зададете координатите на t. X на интервала [a; б] като число, равно на отношението на разликата (x - a) към разликата (b - a). Следователно, a има относителен интервал [a; b] координата 0, и b - 1, средна точка ½.

Ако приемем, че F0 и F1 са еднакви и вземат стойността 1, F2 ще бъде равна на 2, F3 - 3, ..., след това Fn = Fn-1 + Fn-2. Така че, Fn е числото на Фибоначи, а търсенето на Фибоначи е оптималната стратегия за така нареченото последователно максимално търсене, тъй като е доста тясно свързано с тях.

В рамките на оптималната стратегия е обичайно да се избере xn - 1 = Fn - 2: Fn, xn = Fn - 1: Fn. За всеки от двата интервала ([0; xn] или [xn - 1; 1]), всеки от които може да действа като стеснен интервал на неопределеност, точката (наследена) спрямо новия интервал ще има или координатите [Fn - 3: Fn– 1] или [Fn-2: Fn-1]. По-нататък, точка се приема като xn - 2, която по отношение на новата празнина има една от представените координати. Ако използваме F (xn - 2), стойността на функцията, която се наследява от предишната празнина, става възможно да се намали интервала на несигурност и да се предаде наследяването на една стойност на функцията.

На последната стъпка е възможно да се пристъпи към такъв интервал на несигурност като [a; b], докато средната точка е наследена от предишната стъпка. Като x1 се поставя точка, която има относителна координата ½ + ε, а крайният интервал на неопределеност ще бъде [0, ½ + ε] или [½, 1] по отношение на [a; Ь].

На 1-ви етап дължината на този интервал беше намалена до Fn-1: Fn (от един). На финалните стъпки намаляването на дължините на съответните интервали се представя с числата Fn - 2: Fn - 1, Fn - 3: Fn - 2, ..., F2: F3, F1: F2 (1 + 2ε). Така че, дължината на такъв интервал като крайната версия ще приеме стойността (1 + 2ε): Fn.

Ако пренебрегнем ε, асимптотично 1: Fn ще бъде равен на rn, с n → ∞ и r = (√5 - 1): 2, което е приблизително равно на 0.6180.

Трябва да се отбележи, че асимптотично за значимото n всяка следваща стъпка от търсенето на Фибоначи значително стеснява разглеждания интервал с гореспоменатия коефициент. Този резултат трябва да се сравни с 0,5 (коефициентът на стесняване на интервала на неопределеност в рамките на метода на бисекция за намиране на функцията нула).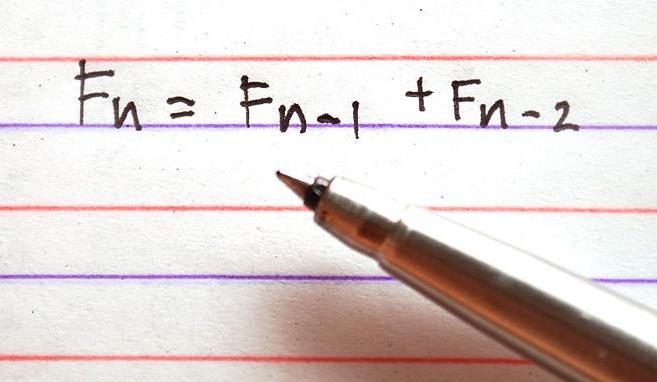

Метод на дихотомия

Ако представим определена целева функция, тогава първо трябва да намерим нейния екстремум в интервала (a; b). За да направите това, оста на абсцисата е разделена на четири еквивалентни части, тогава е необходимо да се определи стойността на въпросната функция в 5 точки. След това изберете минималния сред тях. Екстремумът на функцията трябва да лежи в интервала (a '; b'), който е съседен на минималната точка. Границите на търсене се стесняват 2 пъти. И ако минимумът се намира в м. А или б, тогава се стеснява четири пъти. Новият интервал също е разделен на четири равни сегмента. Поради факта, че стойностите на тази функция в три точки са определени на предишния етап, то тогава е необходимо да се изчисли целевата функция в две точки.

Златен раздел

За значими стойности на n, координатите на точки като xn и xn - 1 са близки до 1 - r, равно на 0.3820, и r ≈ 0.6180. Натискането с тези стойности е много близко до желаната оптимална стратегия.

Ако приемем, че F (0.3820)> F (0.6180), тогава интервалът [0; 0.6180] е очертан. Въпреки това, тъй като 0.6180 * 0.6180 ≈ 0.3820 ≈ xn-1, тогава в тази точка F вече е известно. Следователно, на всеки етап, започвайки от второто, е необходимо само едно изчисление на целевата функция и всяка стъпка намалява дължината на разглеждания интервал с коефициент 0.6180.

За разлика от търсенето на Фибоначи, този метод не изисква фиксиране на числото n още преди началото на търсенето.

"Златният участък" на секцията (a; b) е частта, където съотношението на дължината на r към по-голямата част (a; c) е идентично със съотношението на по-голямата част от r към по-малката, т.е. (a; c) до (c; b). Не е трудно да се предположи, че r се определя от формулата по-горе. Следователно, със значителен n, методът на Фибоначи влиза в това.

Метод за удвояване на стъпка

Същността е в търсенето на посоката на намаляване на целевата функция, движението в тази посока в случай на успешно търсене с постепенно нарастваща стъпка.

Първо, определяме началната координата M0 на функцията F (M), минималната стойност на стъпката h0, посоката на търсене. Тогава дефинираме функцията в m. След това направете стъпка и намерете стойността на тази функция в този момент.

Ако функцията е по-малка от стойността, която е била в предишната стъпка, трябва да извършите следващата стъпка в същата посока, като преди това сте я увеличили 2 пъти. Когато стойността му е по-голяма от предишната, ще трябва да промените посоката на търсене и след това да започнете да се движите в избраната посока със стъпка h0. Представеният алгоритъм може да бъде модифициран.

Многомерни оптимизационни методи

Горният метод с нулев ред не взема под внимание производните на минимизираната функция, така че тяхното използване може да бъде ефективно в случай на трудности при изчисляването на деривати.

Групата от методи от първи ред се нарича градиент, тъй като градиентът на тази функция се използва за установяване на посоката на търсене - вектор, чиито компоненти са частични производни на минимизираната функция по отношение на съответните оптимизирани параметри.

В групата от методи от втори ред се използват 2 производни (тяхната употреба е доста ограничена поради наличието на трудности при изчисляването им).

Списък на методите за безусловна оптимизация

При използване на многомерно търсене без използване на деривати, безусловните методи за оптимизация са както следва:

• Hook and Jeeves (изпълнение на 2 вида търсене - по модел и проучване);
• минимизиране на правилния симплекс (търсене на минималната точка на съответната функция чрез сравняване на всяка отделна итерация с нейните стойности във върховете на симплекса);
• цикличен координатен спускане (използвайки координатни вектори като референтни точки);
• Rosenbrock (въз основа на едномерното минимизиране);
• минимизиране чрез деформиран симплекс (модификация на метода за минимизиране с обикновен симплекс: добавяне на процедура на компресия, разширение).

В ситуацията на използване на деривати в процеса на многоизмерното търсене се отличава методът на най-бързото спускане (най-фундаменталната процедура за минимизиране на диференцируема функция с няколко променливи).

Те също така разграничават такива методи, които използват спрегнати посоки (метод на Davidon-Fletcher-Powell). Нейната същност е представянето на посоките за търсене като Dj * grad (f (y)).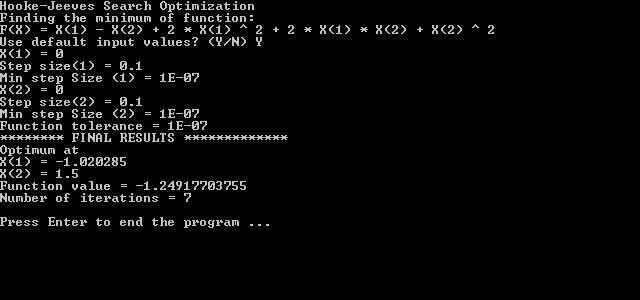

Класификация на математическите методи за оптимизация

Традиционно, въз основа на измерението на функциите (целта), те са:

• с 1 променлива;
• многомерен.

В зависимост от функцията (линейна или нелинейна) има голям брой математически методи, насочени към намиране на екстремум за решаване на проблема.

Според критерия за използване на дериватите, математическите методи за оптимизация се разделят на:

• методи за изчисляване на 1 дериват на целевата функция;
• многомерна (1-ва производна - векторна величина - градиент).

Въз основа на ефективността на изчислението има:

• методи за изчисляване на бързи екстреми;
• опростено изчисление.

Това е условна класификация на разглежданите методи.

Оптимизиране на бизнес процесите

Методите тук могат да бъдат използвани различно, в зависимост от проблемите, които трябва да бъдат решени. Обичайно е да се избират следните методи за оптимизиране на бизнес процесите:

• изключения (намаляване на съществуващите нива на процесите, премахване на причините за интерференция и входен контрол, намаляване на транспортните маршрути);
• опростяване (улесняване на преминаването на поръчката, намаляване на сложността на продуктовата структура, разпределение на работата);
• стандартизация (използване на специални програми, методи, технологии и др.);
• ускоряване (паралелно инженерство, стимулиране, оперативно проектиране на прототипи, автоматизация);
• промяна (промени в областта на суровините, технологиите, методите на работа, местоположението на персонала, работните системи, количеството на поръчката, процедурата на обработка);
• осигуряване на оперативна съвместимост (по отношение на организационни единици, персонал, система на работа);
• подбор и включване (относно необходимите процеси, компоненти).

Данъчна оптимизация: методи

Руското законодателство предоставя на данъкоплатците много богати възможности за намаляване на размера на данъците, поради което е обичайно да се избират такива методи, които имат за цел да ги сведат до минимум, като общи (класически) и специални.

Общите методи за данъчна оптимизация са както следва:

• разработване на счетоводна политика на дружеството с максимално използване на възможностите, предоставени от руското законодателство (процедура за отписване на МБП, избор на метод за изчисляване на приходите от продажба на стоки и др.);
• оптимизиране чрез договор (сключване на привилегировани сделки, ясна и компетентна употреба на текстове и др.);
• използването на различни видове обезщетения, данъчни облекчения.

Втората група методи могат да се използват и от всички фирми, но те все още имат доста тесен обхват. Специалните методи за данъчна оптимизация са както следва:

• подмяна на отношенията (операцията, която предвижда обременително данъчно облагане, се заменя с друга, която ви позволява да постигнете подобна цел, но в същото време да използвате преференциална данъчна процедура).
• разделяне на отношенията (замяна само на част от търговска сделка);
• отсрочване на плащането на данъци (отлагане на момента на настъпване облагаема стока за друг календарен период);
• пряко намаляване на облагаемия обект (премахване на много облагаеми сделки или имущество, без да има отрицателно въздействие върху основната икономическа дейност на дружеството).