Триизмерно пространство: вектори, координати

Дори от училищния курс по алгебра и геометрия знаем за концепцията за триизмерното пространство. Ако разбираме, терминът "триизмерно пространство" се определя като координатна система с три измерения (всеки знае това). В действителност е възможно да се опише обект с обем с помощта на дължина, ширина и височина в класическия смисъл. Въпреки това, нека, както се казва, копаят малко по-дълбоко.

Какво е триизмерно пространство

Както вече стана ясно, разбирането на триизмерното пространство и обектите, които могат да съществуват вътре в него, се определя от три основни понятия. Вярно е, че в случая с една точка те са точно три стойности, а в случая на прави, извити, прекъснати линии или обемни обекти, съответните координати могат да бъдат по-големи.

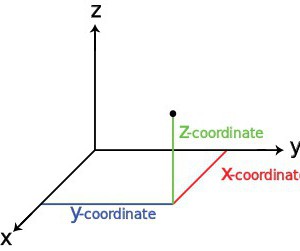
В този случай всичко зависи от вида на обекта и от приложената координатна система. Днес, декартовата система, понякога наричана още правоъгълна, се счита за най-често срещаната (класическа). Тя и някои други видове ще бъдат обсъдени по-късно.

Наред с другите неща, тук е необходимо да се прави разлика между абстрактни понятия (ако е възможно да се каже така, безформени) като точки, прави линии или равнини и фигури, които имат крайни размери или дори обем. За всяка от тези дефиниции има и собствени уравнения, описващи тяхното възможно положение в триизмерното пространство. Но сега не става въпрос за това.

Концепцията за точка в триизмерното пространство

Като начало определяме какво е точката в триизмерното пространство. Като цяло, тя може да бъде наречена някаква основна единица, която определя всяка плоска или триизмерна фигура, линия, сегмент, вектор, равнина и т.н.

Самата точка се характеризира с три основни координати. За тях в правоъгълна система се използват специални водачи, наречени оси X, Y и Z, като първите две оси се използват за изразяване на хоризонталната позиция на обекта, а третата се отнася до вертикалната спецификация на координатите. Естествено, за удобство на изразяване на позицията на обект спрямо нулевите координати в системата се приемат положителни и отрицателни стойности. Днес обаче можете да намерите други системи.

Разнообразие на координатни системи

Както вече споменахме, правоъгълната координатна система, създадена от Декарт, днес е основната. Въпреки това, в някои техники за определяне на местоположението на обект в триизмерно пространство се използват някои други разновидности.

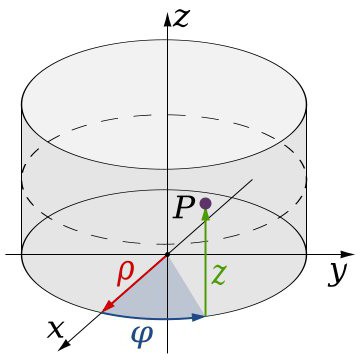
Най-известни са цилиндричните и сферичните системи. Разликата от класическата е, че когато се определят същите три стойности, които определят местоположението на точка в триизмерното пространство, една от стойностите е ъглова. С други думи, в такива системи се използва кръг, съответстващ на ъгъл от 360 градуса. Оттук и специфичната задача на координатите, включително такива елементи като радиус, ъгъл и образуваща. Координатите в триизмерното пространство (система) от този тип се подчиняват на малко по-различни закони. Тяхната задача в този случай се контролира от правилото на дясната ръка: ако комбинирате палеца и показалеца с осите X и Y, съответно, останалите пръсти в изкривено положение ще посочат посоката на оста Z.

Концепцията за линия в триизмерното пространство

Сега няколко думи за това какво представлява права линия в триизмерното пространство. Базирайки се на основната концепция на права линия, това е един вид безкрайна линия, изтеглена през точка или две, без да се брои набор от точки, разположени в последователност, която не променя директното преминаване на линията през тях.

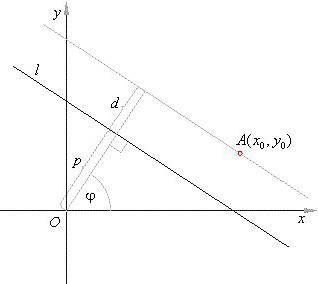
Ако погледнете линия, прокарана през две точки в триизмерно пространство, ще трябва да вземете под внимание трите координати на двете точки. Същото се отнася и за сегментите и векторите. Последните определят основата на триизмерното пространство и неговото измерение.

Дефиниране на вектори и базата на триизмерното пространство

Както обикновено се смята, в триизмерната координатна система може да има три основни вектора, които определят базата. Освен това базите със съответните независими три вектора могат да бъдат безбройни.

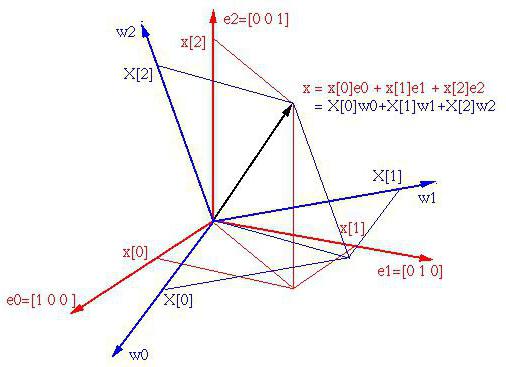
Забележете, че може да има само три вектора, но тук можете да дефинирате колкото тройки вектори. Размерът на пространството се определя от броя на линейно независимите вектори (в нашия случай три). И пространството, в което има краен брой такива вектори, се нарича крайномерно.

Зависими и независими вектори

Що се отнася до дефинирането на зависими и независими вектори, векторите, които са проекции (например векторите с X-ос, проектирани по Y-оста), се считат за линейно независими.

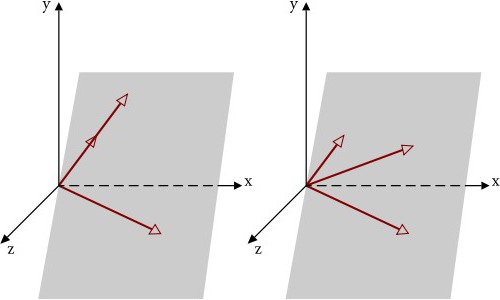
Както вече е ясно, всеки четвърти вектор е зависим (теорията на линейните пространства). Но три независими вектора в триизмерното пространство не трябва непременно да лежат в една и съща равнина. В допълнение, ако дефинираме независими вектори в триизмерното пространство, те не могат да бъдат, така да се каже, едно продължение на другото. Както вече е ясно, в случая, който разглеждаме с три измерения, съгласно общата теория, могат да бъдат конструирани само три тройки от линейно независими вектори в дадена координатна система (без значение какъв тип).

Равнина в триизмерно пространство

Ако разгледаме концепцията за равнина, без да навлизаме в математически дефиниции, за по-простото разбиране на този термин, такъв обект може да се разглежда само като двуизмерен. С други думи, това е безкрайна колекция от точки, където една от координатите е константа (константа).

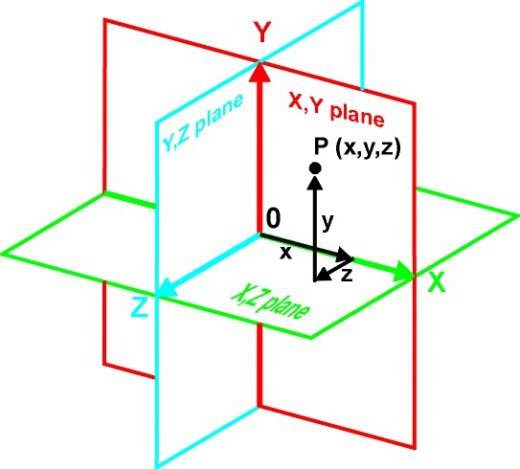
Например, една равнина може да се нарече произволен брой точки с различни координати по осите X и Y, но със същите координати по оста Z. Във всеки случай, една от триизмерните координати остава непроменена. Това обаче е, така да се каже, общ случай. В някои ситуации триизмерното пространство може да се пресича с равнина по всички оси.

Има ли повече от три измерения

Интересен е въпросът за това, колко измервания могат да съществуват. Смята се, че не живеем в триизмерно от класическата гледна точка на пространството, а в четириизмерно. В допълнение към добре известните дължини, ширини и височини, това пространство включва и живота на обекта, а времето и пространството са взаимосвързани доста силно. Това е доказано от Айнщайн в неговата теория на относителността, въпреки че това се отнася повече до физиката, отколкото до алгебрата и геометрията.

Друг интересен факт е, че днес учените вече са доказали съществуването на поне дванадесет измерения. Разбира се, далеч от всеки ще може да разбере какво са, тъй като се отнася по-скоро до определена абстрактна област, която е извън човешкото възприемане на света. Въпреки това фактът остава. И не за нищо много антрополози и историци твърдят, че нашите предци биха могли да имат някои специфично разработени сетивни органи като третото око, което е помогнало за възприемането на многоизмерната реалност, а не само за триизмерното пространство.

Между другото, днес има доста мнения за факта, че екстрасензорното възприятие също е едно от проявленията на възприемането на многоизмерния свят и може да се намерят доста доказателства.

Забележете, че съвременните основни уравнения и теореми описват многоизмерни пространства, които са различни от нашия четириизмерен свят, също не винаги е възможно. И науката в тази област е свързана повече с областта на теориите и предположенията, отколкото с това, което може да бъде ясно усетено или, така да се каже, докоснато или видяно от първа ръка. Независимо от това, непряко доказателство за съществуването на многоизмерни светове, в които може да има четири или повече измерения, днес е без съмнение.

заключение

Като цяло, накратко разгледахме основните понятия, свързани с триизмерното пространство и основните дефиниции. Естествено, има много специални случаи, свързани с различни координатни системи. В допълнение, ние се опитахме да не влезем в дивата природа на математиката, за да обясним основните термини, само така, че свързаният с тях въпрос е разбираем за всеки ученик (така да се каже, обяснението е „на пръстите“).

Въпреки това изглежда, че дори и от такива прости интерпретации може да се заключи, че математическият аспект на всички компоненти, включени в основния училищен курс по алгебра и геометрия.