Повърхността на призмата. Площта на основата и страничната повърхност. Основата на триъгълната призма

В пространствената геометрия, когато се решават проблеми с призми, често има проблем с изчисляването на площта на страните или лицата, които образуват тези триизмерни форми. Тази статия е посветена на въпроса за определяне на площта на основата на призмата и нейната странична повърхност.

Фигура на призмата

Преди да пристъпим към разглеждане на формулите за базовата област и повърхността на една или друга призма, е необходимо да разберем коя цифра под въпрос.

Призма в геометрията е пространствена фигура, състояща се от два успоредни полигона, които са равни, и няколко четириъгълника или успоредника. Числото на последния винаги е равно на броя на върховете на един полигон. Например, ако една фигура се формира от два паралелни n-gons, тогава броят на паралелограмите ще бъде n.

Паралелограмните свързващи n-gons се наричат ​​страни на призмата и тяхната обща площ е площта на страничната повърхност на фигурата. Самите n-gons се наричат ​​бази.

Горната фигура показва пример на призма, направена от хартия. Жълтият правоъгълник е неговата горна основа. На второто място стои същата фигура на земята. Червените и зелените правоъгълници са странични лица.

Какви призми има?

Има няколко вида призми. Всички те се различават един от друг само по два параметъра:

• тип n-gon, формиращ основата;
• ъгълът между n-ъгъла и страничните повърхности.

Например, ако базите са триъгълници, тогава призмата се нарича триъгълна, ако четириъгълниците, както и в предишната фигура, се наричат ​​четириъгълна призма и така нататък. В допълнение, n-ъгъла може да бъде изпъкнал или вдлъбнат, тогава това свойство също се добавя към името на призмата.

Ъгълът между страничните повърхности и основата може да бъде или прав, или остър или тъп. В първия случай те говорят за правоъгълна призма, а във втория - за наклонена или наклонена.

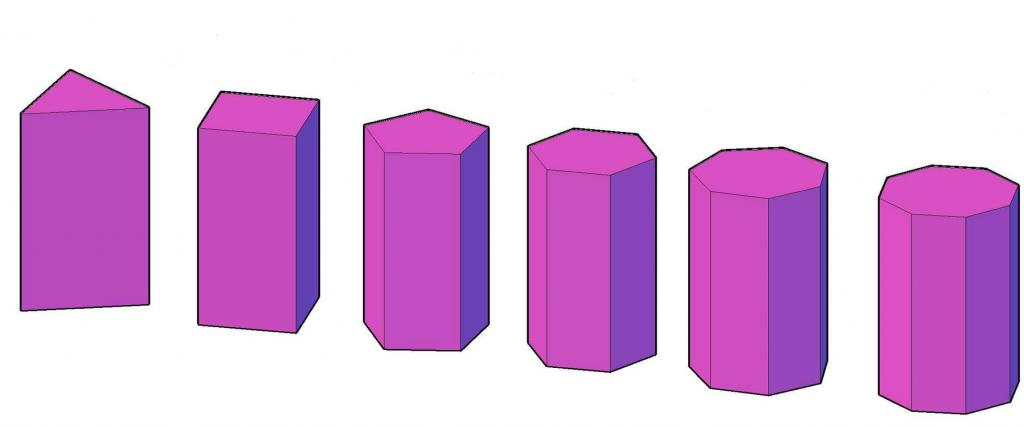
В специален вид фигури разпределят правилната призма. Те имат най-висока симетрия сред другите призми. То ще бъде правилно, само ако е правоъгълно и неговата основа е правилен n-gon. Фигурата по-долу показва набор от правилни призми, в които броят на страните на n-ъгъла варира от три до осем.

Повърхността на призмата

Под повърхността на разглежданите фигури от произволен тип разбират съвкупността от всички точки, които принадлежат на лицата на призмата. Повърхността на призмата е удобна за изследване, като се има предвид нейното развитие. По-долу е даден пример за такова почистване за триъгълна призма.

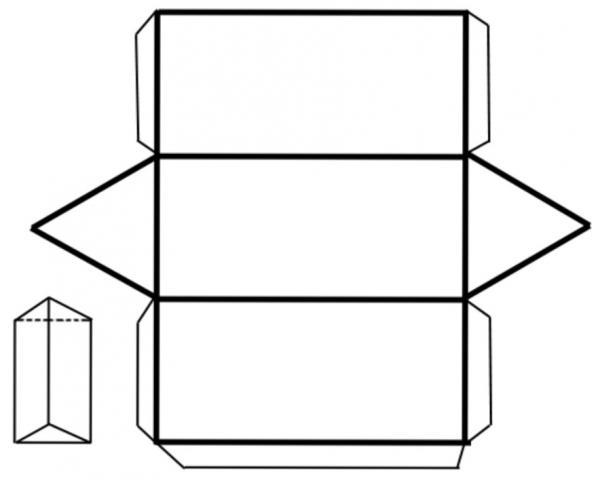
Вижда се, че цялата повърхност е оформена от два триъгълника и три правоъгълника.

В случая на призма от общ тип, нейната повърхност ще се състои от две n-въглищни бази и n четиристранни.

Нека разгледаме по-подробно въпроса за изчисляване на повърхността на призми от различен тип.

Основата на призмата е правилна

Може би най-простата задача при работа с призми е проблемът с намирането на областта на основата на правилната фигура. Тъй като тя се формира от n-гон, в който всички ъгли и дължини на страните са еднакви, тя винаги може да бъде разделена на еднакви триъгълници, в които са известни ъглите и страните. Общата площ на триъгълниците ще бъде площта на n-gon.

Друг начин за определяне на част от повърхностната площ на призмата (основа) е да се използва известна формула. Той има следната форма:

S _n = n / 4 * a ² * ctg (pi / n)

Това означава, че областта _{Sn на} n-ъгъла е еднозначно определена от познанието за дължината на неговата страна a. Някои трудности при изчисляването по формулата могат да бъдат изчислението на котангенса, особено когато n> 4 (за n≤4, котангенсните стойности са таблични данни). За да се определи тази тригонометрична функция, се препоръчва да се използва калкулатор.

Когато се формулира геометричен проблем, трябва да се внимава, тъй като може да се наложи да се намери площта на основите на призмата. Тогава получената от формулата стойност трябва да се умножи по две.

Основата на триъгълната призма

Използвайки примера на триъгълна призма, ще разгледаме как да намерим областта на основата на тази фигура.

Първо, помислете за простия случай - правилната призма. Площта на основата се изчислява с помощта на формулата, дадена в горния параграф, трябва да се замени с n = 3. Получаваме:

S ₃ = 3/4 * a ² * ctg (pi / 3) = 3/4 * a ² * 1 / =3 = √ 3/4 * a ²

Остава да се заменят конкретните стойности на дължината а на страната на равностранен триъгълник в израза, за да се получи площта на една база.

Сега да предположим, че има призма, чиято база е произволен триъгълник. Двете му страни, а и b, и ъгълът между тях, α, са известни. Тази цифра е показана по-долу.

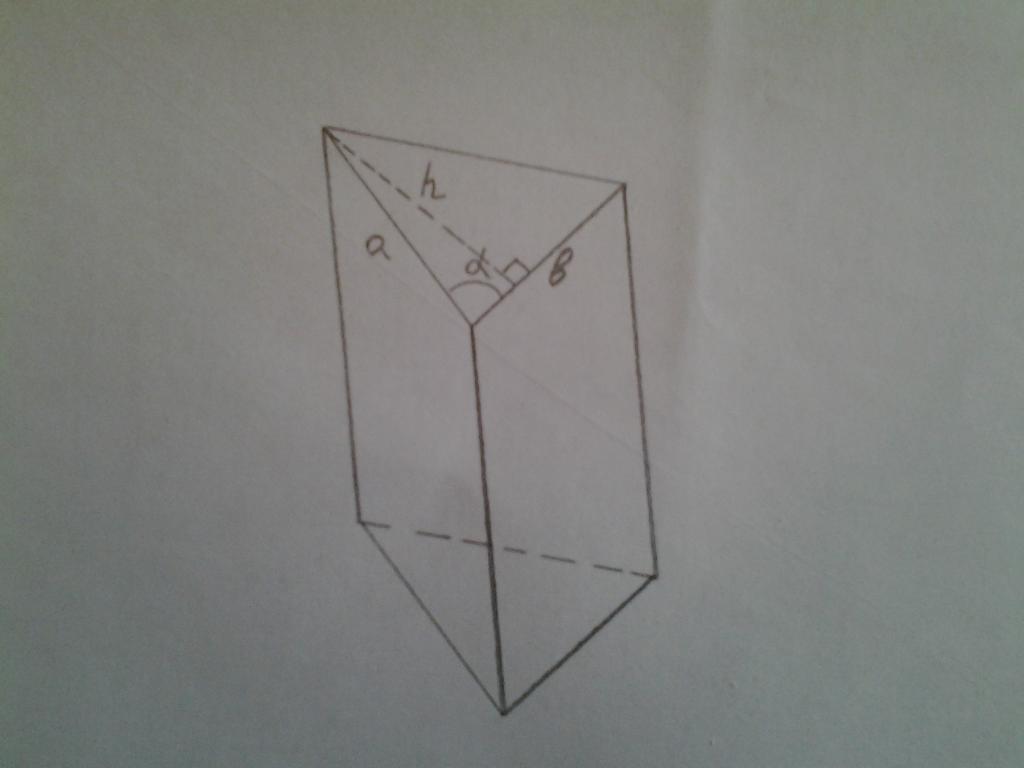
Как в този случай да се намери площта на основата на призмата триъгълна? Трябва да се помни, че площта на всеки триъгълник е равна на половината от произведението на страната, а височината - от тази страна. Фигурата показва височината h на страната b. Дължината h съответства на произведението на синуса на ъгъла алфа и дължината на страната a. Тогава площта на целия триъгълник е равна на:

S = 1/2 * b * h = 1/2 * b * a * sin (α)

Това е площта на основата на изобразената триъгълна призма.

Странична повърхност

Разбрахме как да намерим областта на основата на призмата. Страничната повърхност на тази фигура винаги се състои от паралелограми. За директни призми паралелограмите стават правоъгълници, така че общата им площ се изчислява лесно:

S = ∑ _{i = 1} ⁿ (a _i * b)

Тук b е дължината на страничния ръб, a _i е дължината на страната на i-тия правоъгълник, която съвпада с дължината на страната на n-ъгъла. В случай на нормална n-ъглова призма получаваме прост израз:

S = n * a * b

Ако призмата е наклонена, тогава, за да определите площта на неговата странична повърхност, направете перпендикулярно нарязване, изчислете нейния периметър Р _sr и го умножете по дължината на страничния ръб.

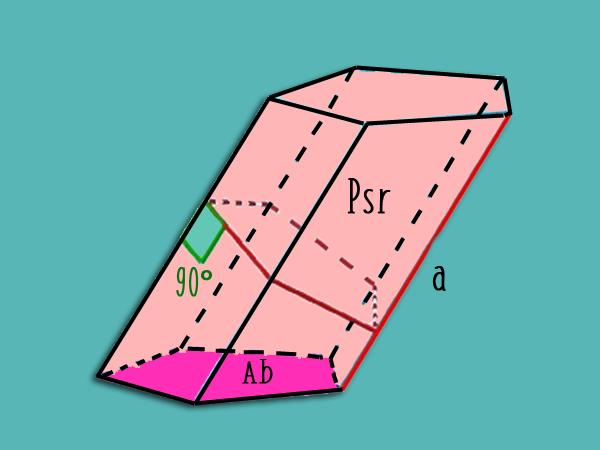
Фигурата по-горе показва как да се направи този парче за наклонена петоъгълна призма.